Anonymous 1123

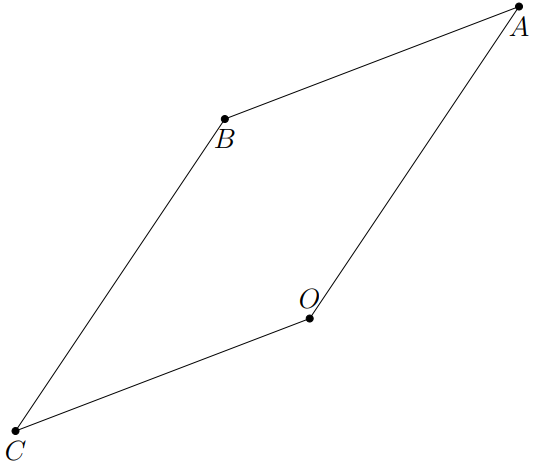
I want to draw a parallelogram in the plane has equation `7 x-4 y+z=0`. I draw by choosing four vertices on the plane.
I tried
```
\documentclass[tikz,border=1mm,12pt]{standalone}
\usepackage{tikz-3dplot}
\begin{document}
\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords]
\path
(0, 0, 0) coordinate (O)
(1, 3, 5) coordinate (A)
(-2, -4, -2) coordinate (C)
(-1, -1, 3) coordinate (B);
\draw (O) -- (A) -- (B) -- (C) -- cycle;
\foreach \p in {A,B,C,O}
\draw[fill=black] (\p) circle (1.5 pt);
\foreach \p/\g in {A/-90,B/-90,C/-90,O/90}
\path (\p)+(\g:3mm) node{$\p$};
\end{tikzpicture}
\end{document}
```
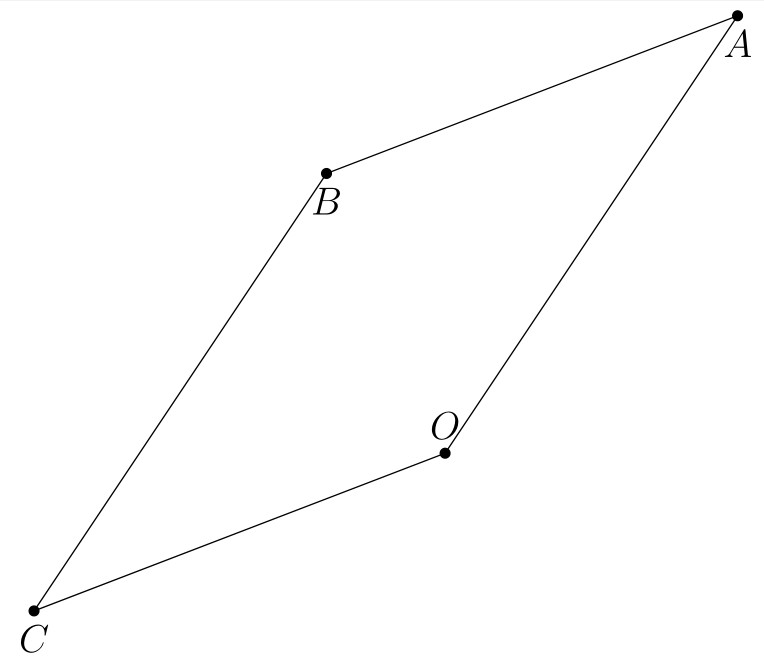
How to make a macro to draw a parallelogram in plane has given equation without knowing coordinates of vertices?
Top Answer
user 3.14159

The output of the following is not pretty but it may do in principle what you want. Given the normal `n` of the plane, two vectors that are orthogonal to `n` and mutually orthogonal is computed. These vectors can be used to draw the parallelogram.
````
\documentclass[tikz,border=1mm,12pt]{standalone}
\usepackage{tikz-3dplot}
\pgfmathdeclarefunction{normalcandidate}{3}{%
\begingroup%
\pgfmathtruncatemacro{\icase}{(abs(#1)>0)+2*(abs(#2)>0)+4*(abs(#3)>0)}%
\ifcase\icase
\message{All three coordinates are zero. No normal can be computed.^^J}%
\edef\pgfmathresult{0,0,0}%
\or
\edef\pgfmathresult{0,1,0}%
\or
\edef\pgfmathresult{0,0,1}%
\or
\edef\pgfmathresult{0,0,1}%
\or
\edef\pgfmathresult{1,0,0}%
\or
\edef\pgfmathresult{0,1,0}%
\or
\edef\pgfmathresult{z,0,0}%
\or
\pgfmathsetmacro{\normalization}{(#1)*(#1)+(#2)*(#2)}%
\pgfmathsetmacro{\nx}{-1*(#2)/sqrt(\normalization)}%
\pgfmathsetmacro{\ny}{#1/sqrt(\normalization)}%
\edef\pgfmathresult{\nx,\ny,0}%
\fi
%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%
\begin{document}
\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords]
% compute one vector, p_1, that is orthogonal to the plane normal, n=(7,-4,1)
% the convention here is that normalcandidate returns vectors of length 1
\pgfmathsetmacro{\mynormalA}{normalcandidate(7,-4,1)}
% get the second plane vector as p_2=n x p_1
\edef\temp{\noexpand\tdplotcrossprod(7,-4,1)(\mynormalA)}
\temp
\path
(0, 0, 0) coordinate (O)
(\tdplotresx,\tdplotresy,\tdplotresz) coordinate (A) % p_2
({\tdplotresx+4*({\mynormalA}[0])},{\tdplotresy+(4*{\mynormalA}[1])},%
{\tdplotresz+4*({\mynormalA}[2])}) coordinate (B) % p_1 + p_2
({4*({\mynormalA}[0])},{4*({\mynormalA}[1])},{4*({\mynormalA}[2])})
coordinate (C); % p_2
\draw (O) -- (A) -- (B) -- (C) -- cycle;
\foreach \p in {A,B,C,O}
\draw[fill=black] (\p) circle (1.5 pt);
\foreach \p/\g in {A/-90,B/-90,C/-90,O/90}
\path (\p)+(\g:3mm) node{$\p$};
\end{tikzpicture}
\end{document}
````
The problem is that we can rotate the vectors in the plane they span and get another set of valid vectors. The automatically computed ones are usually not the prettiest possible choices. More precisely, unless we have precise criteria for the pretty vectors that we can code in, the computer will just pick some valid candidates.
Answer #2
joulev

I'm not sure if I really understand your question. If you want to draw a parallelogram given three points, you can use this trick. (I personally find it very helpful when drawing scientific figures. It doesn't depend on whether you are using 3d or not.)
It uses `calc` to perform some calculations which is essentially B=A+vector(OC).
```
% arara: pdflatex
\documentclass[tikz,border=1mm,12pt]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{calc}
\begin{document}
\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords]
\path
(0, 0, 0) coordinate (O)
(1, 3, 5) coordinate (A)
(-2, -4, -2) coordinate (C);
\coordinate (B) at ($(A)+(C)-(O)$);
\draw (O) -- (A) -- (B) -- (C) -- cycle;
\foreach \p in {A,B,C,O}
\draw[fill=black] (\p) circle (1.5 pt);
\foreach \p/\g in {A/-90,B/-90,C/-90,O/90}
\path (\p)+(\g:3mm) node{$\p$};
\end{tikzpicture}
\end{document}
```