How about this one?


```

\documentclass[tikz,border=3mm]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.16}
\begin{document}
\begin{tikzpicture}
\begin{axis}[hide axis,colormap={bluered}{color=(red) color=(blue)}] 
 \addplot[domain=0:4,samples=401,smooth,very thick,mesh,point meta=y] 
 	({1.5*(x+0.4*x*x)+x*sin(x*360)},{-x*cos(360*x)});
\end{axis}
\end{tikzpicture}
\end{document}
```

![Screen Shot 2020-03-16 at 3.52.09 PM.png](/image?hash=e7208e5c230631fe2505bfc214e2c51f1f5c5cb7257cede37499c9bdf1fa871b)

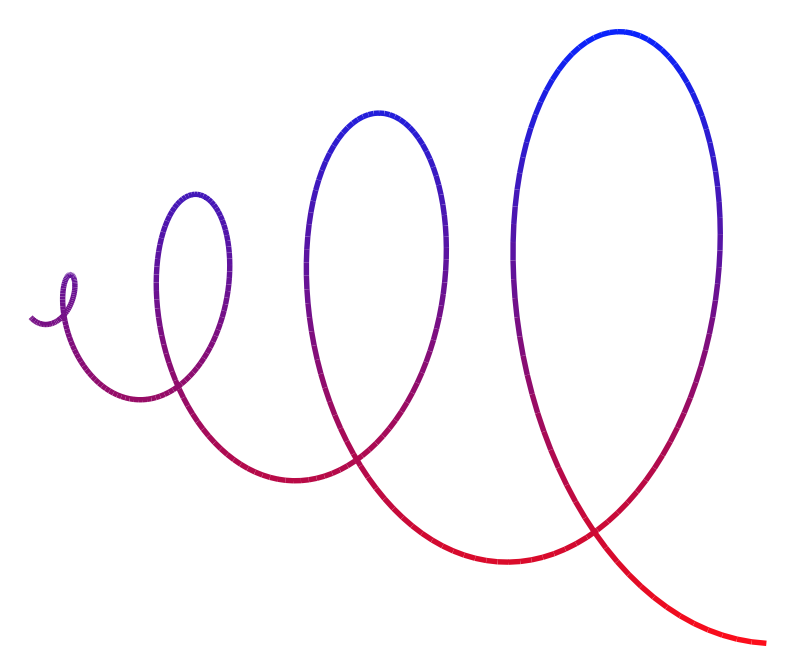
Another way to get the color gradient is to use `path fading`. 

```

\documentclass[border=3mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{fadings,calc,arrows.meta,bending}
\begin{document}
\begin{tikzfadingfrompicture}[name=temp]
\begin{scope}[local bounding box=pft]
 \draw[transparent!0,-{Stealth[length=3mm,width=3.2mm,bend]},line width=1.2pt]  
	 plot[variable=\x,domain=-0.15:4,smooth,samples=91]
  ({1.5*(\x+0.5*\x*\x)+(1+\x)*sin(\x*360)},{-(1+\x)*cos(360*\x)});
\end{scope}  
\end{tikzfadingfrompicture}%
\begin{tikzpicture}
\path[path fading=temp,fit fading=false,top color=blue,bottom color=red]
 let \p1=($(pft.north east)-(pft.south west)$) in
 (-\x1/2,-\y1/2) rectangle ++(\x1,\y1);
\end{tikzpicture}
\end{document}
```

![Screen Shot 2020-03-16 at 4.26.08 PM.png](/image?hash=f75561db0cdebb0ba261f01983baafbabf690f1a072857b62cb6009af268c934)

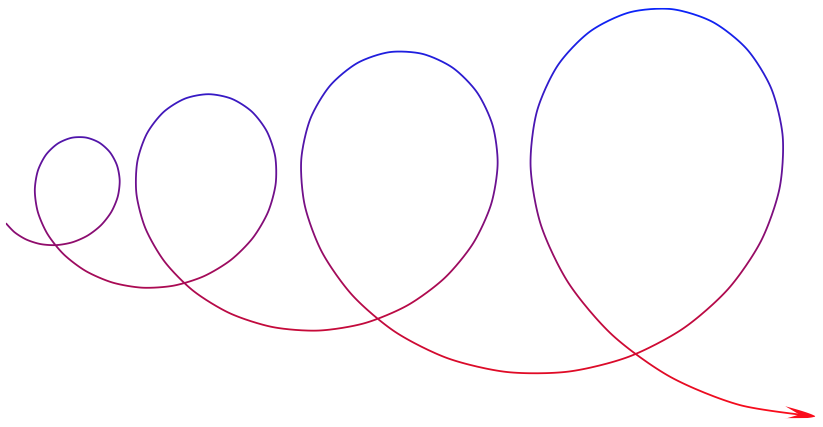
You can also use `decorations` and Ti*k*Z, but the solution is very fragile because one can easily get `dimension too large` errors.

```

\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{decorations,arrows.meta,bending}
\begin{document}

\pgfkeys{/pgf/decoration/.cd,
         start color/.store in=\startcolor,
         start color=black,
         end color/.store in=\endcolor,
         end color=black,
         varying line width steps/.initial=100
}
\pgfdeclaredecoration{width and color change}{initial}{
 \state{initial}[width=0pt, next state=line, persistent precomputation={%
   \pgfmathparse{\pgfdecoratedpathlength/\pgfkeysvalueof{/pgf/decoration/varying line width steps}}%
   \let\increment=\pgfmathresult%
   \def\x{0}%
 }]{}
 \state{line}[width=\increment pt,   persistent postcomputation={%
   \pgfmathsetmacro{\x}{\x+\increment}
   },next state=line]{%
   \pgfmathparse{ifthenelse(\x<\pgfdecoratedpathlength-5mm,varyinglw(100*(\x/\pgfdecoratedpathlength)),
    varyinglw(100*((\pgfdecoratedpathlength-5mm)/\pgfdecoratedpathlength))*(\pgfdecoratedpathlength-\x)/14) )}
   \pgfsetlinewidth{\pgfmathresult pt}%
   \pgfpathmoveto{\pgfpointorigin}%
   \pgfmathsetmacro{\steplength}{1.4*\increment}
   \pgfpathlineto{\pgfqpoint{\steplength pt}{0pt}}%
   \pgfmathsetmacro{\y}{100*(\x/\pgfdecoratedpathlength)}
   \pgfsetstrokecolor{\endcolor!\y!\startcolor}%
   \pgfusepath{stroke}%
 }
 \state{final}{%
   \pgfsetlinewidth{\pgflinewidth}%
   \pgfpathmoveto{\pgfpointorigin}%
   \pgfmathsetmacro{\y}{100*(\x/\pgfdecoratedpathlength)}
   \color{\endcolor!\y!\startcolor}%
   \pgfusepath{stroke}% 
 }
}


\begin{tikzpicture}[varying arrow/.style={-{Stealth[length=4mm,width=3.2mm,bend]},color=\endcolor,
postaction={/utils/exec=\pgfsetarrows{-},decorate,decoration={width and color change}}
}]
\begin{scope}[declare function={varyinglw(\x)=1+2*\x/100;}]
\draw[varying arrow,/pgf/decoration/varying line width steps=1801,
/pgf/decoration/start color=red,/pgf/decoration/end color=blue]
 plot[variable=\x,domain=0:4,smooth,samples=91]
 ({1.5*(\x+0.4*\x*\x)+(1+\x)*sin(\x*360)},{-(1+\x)*cos(360*\x)});
\end{scope}
\end{tikzpicture}
\end{document} 
```

![Screen Shot 2020-03-16 at 4.08.36 PM.png](/image?hash=cad510bba100d267e07f5b1b8cb435b981e4e20ca5a1cfbc0c0336f534716280)