JohnPaul

I want to align content in the diagbox environment. This is my code
```
\documentclass{article}
\usepackage{tabularray}
\UseTblrLibrary{diagbox}
\UseTblrLibrary{varwidth}
\usepackage{float}
\usepackage{enumitem}
\usepackage{ninecolors}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{siunitx}
\usepackage{xurl}
\sisetup{output-decimal-marker={,}}
\UseTblrLibrary{siunitx}
\usepackage[paperwidth=20.5cm, paperheight=29cm, left=1.7cm,right=1.7cm,top=1.8cm,bottom=1.7cm]{geometry}
\begin{document}
\begin{table}[H]
\centering
\begin{tblr}{
colspec={*{10}{c}},
row{1}={olive9,mode=text},
vlines,hlines,
hline{1,2,Z}={solid},
cells={mode=dmath}
}
\diagbox{\begin{varwidth}{2.8cm} \centering Trigonometric values \end{varwidth}}{\text{Angle } \alpha}
& 0^\circ & 30^\circ & 45^\circ & 60^\circ & 90^\circ & 120^\circ & 135^\circ & 150^\circ & 180^\circ \\
\sin\alpha
& 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1
& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \\
\cos\alpha
& 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0
& -\dfrac{1}{2} & -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{3}}{2} & -1 \\
\tan\alpha
& 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & ||
& -\sqrt{3} & -1 & -\dfrac{\sqrt{3}}{3} & 0 \\
\cot\alpha
& || & \sqrt{3} & 1 & \dfrac{\sqrt{3}}{3} & 0
& -\dfrac{\sqrt{3}}{3} & -1 & -\sqrt{3} & || \\
\end{tblr}
\end{table}
\end{document}
```
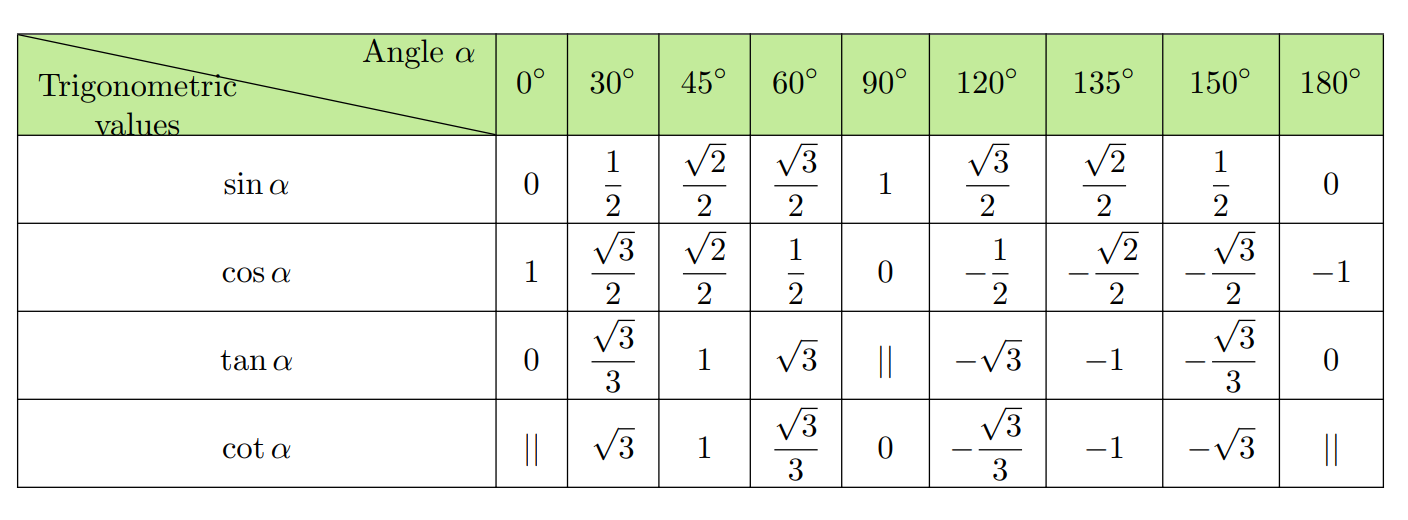
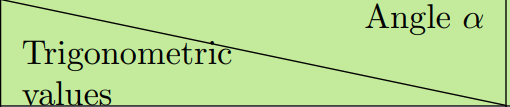
In this figure, the diagonal passes through the dot of the letter i and very close to the letter C. How can I avoid this?
Top Answer
samcarter

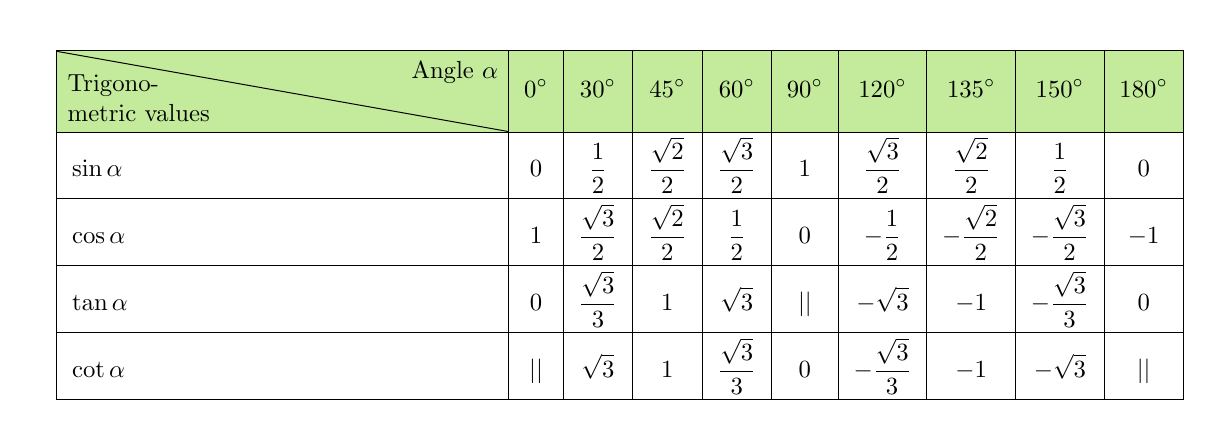
As a quick and dirty hack, you could manually add a line break:
```
\documentclass{article}
\usepackage{tabularray}
\UseTblrLibrary{diagbox}
\UseTblrLibrary{varwidth}
\usepackage{float}
\usepackage{enumitem}
\usepackage{ninecolors}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{siunitx}
\usepackage{xurl}
\sisetup{output-decimal-marker={,}}
\UseTblrLibrary{siunitx}
\usepackage[paperwidth=20.5cm, paperheight=29cm, left=1.7cm,right=1.7cm,top=1.8cm,bottom=1.7cm]{geometry}
\begin{document}
\begin{table}[H]
\centering
\begin{tblr}{
colspec={*{10}{c}},
row{1}={olive9,mode=text},
vlines,hlines,
hline{1,2,Z}={solid},
cells={mode=dmath}
}
\diagbox{\begin{varwidth}{2.8cm} \centering Trigono-\\ metric values \end{varwidth}}{\text{Angle } \alpha}
& 0^\circ & 30^\circ & 45^\circ & 60^\circ & 90^\circ & 120^\circ & 135^\circ & 150^\circ & 180^\circ \\
\sin\alpha
& 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1
& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \\
\cos\alpha
& 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0
& -\dfrac{1}{2} & -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{3}}{2} & -1 \\
\tan\alpha
& 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & ||
& -\sqrt{3} & -1 & -\dfrac{\sqrt{3}}{3} & 0 \\
\cot\alpha
& || & \sqrt{3} & 1 & \dfrac{\sqrt{3}}{3} & 0
& -\dfrac{\sqrt{3}}{3} & -1 & -\sqrt{3} & || \\
\end{tblr}
\end{table}
\end{document}
```
For more control, you could use tikz:
```
\documentclass{article}
\usepackage{tabularray}
\UseTblrLibrary{diagbox}
\UseTblrLibrary{varwidth}
\UseTblrLibrary{tikz}
\usepackage{float}
\usepackage{enumitem}
\usepackage{ninecolors}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{siunitx}
\usepackage{xurl}
\sisetup{output-decimal-marker={,}}
\UseTblrLibrary{siunitx}
\usepackage[paperwidth=20.5cm, paperheight=29cm, left=1.7cm,right=1.7cm,top=1.8cm,bottom=1.7cm]{geometry}
\begin{document}
\begin{table}[htbp]
\centering
\begin{tblrtikzabove}
\tikzset{inner sep=4pt}
\draw (1-1.north west) -- (1-1.south east);
\node[anchor=south west,text width=2.5cm,align=left] at (1-1.south west) {Trigono-\\ metric values };
\node[anchor=north east] at (1-1.north east) {Angle $\alpha$};
\end{tblrtikzabove}%
\begin{tblr}{
colspec={Q[6cm]*{9}{c}},
row{1}={olive9,mode=text,ht=1cm},
vlines,hlines,
hline{1,2,Z}={solid},
cells={mode=dmath}
}
& 0^\circ & 30^\circ & 45^\circ & 60^\circ & 90^\circ & 120^\circ & 135^\circ & 150^\circ & 180^\circ \\
\sin\alpha
& 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1
& \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \\
\cos\alpha
& 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0
& -\dfrac{1}{2} & -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{3}}{2} & -1 \\
\tan\alpha
& 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & ||
& -\sqrt{3} & -1 & -\dfrac{\sqrt{3}}{3} & 0 \\
\cot\alpha
& || & \sqrt{3} & 1 & \dfrac{\sqrt{3}}{3} & 0
& -\dfrac{\sqrt{3}}{3} & -1 & -\sqrt{3} & || \\
\end{tblr}
\end{table}
\end{document}
```