निरंजन

Suppose there are two sequences and I want them to always have the same length in order to match their items later. I want two separate commands for adding items to them. I came up with this:
```
\documentclass{article}
\begin{document}
\ExplSyntaxOn
\cs_new:Npn \__add_to_tmpa:n #1 {
\seq_put_right:Nn \l_tmpa_seq { #1 }
}
\cs_new:Npn \__add_to_tmpb:n #1 {
\prg_replicate:nn {
(
\seq_count:N \l_tmpa_seq - \seq_count:N \l_tmpb_seq
)
-
1
} {
\seq_put_right:Nn \l_tmpb_seq { \q_nil }
}
\seq_put_right:Nn \l_tmpb_seq { #1 }
}
\__add_to_tmpa:n {a} \__add_to_tmpb:n {a}
\__add_to_tmpa:n {b}
\__add_to_tmpa:n {c}
\__add_to_tmpa:n {d}
\__add_to_tmpa:n {e}
\__add_to_tmpa:n {f} \__add_to_tmpb:n {f}
\seq_show:N \l_tmpa_seq
\seq_show:N \l_tmpb_seq
\ExplSyntaxOff
\end{document}
```
It results in:
```text
The sequence \l_tmpa_seq contains the items (without outer braces):
> {a}
> {b}
> {c}
> {d}
> {e}
> {f}.
The sequence \l_tmpb_seq contains the items (without outer braces):
> {a}
> {\q_nil }
> {\q_nil }
> {\q_nil }
> {\q_nil }
> {f}.
```
and this is correct considering my need.
Does this look okay? Am I violating any standard conventions? Is there any further optimisation possible?
Top Answer
Skillmon

With the conditions
- that seq A is always assigned first and
- that seq A is guaranteed to have more meaningful entries than seq B (which somewhat follows from the first point)
you can optimise your code a bit:
```
\documentclass{article}
\usepackage{array,booktabs}
\ExplSyntaxOn
\cs_new_protected:Npn \__niranjan_add_to_tmpa:n
{
\seq_put_right:Nn \l_tmpb_seq { \q_nil }
\seq_put_right:Nn \l_tmpa_seq
}
\cs_new_protected:Npn \__niranjan_add_to_tmpb:n
{ \seq_set_item:Nnn \l_tmpb_seq { -1 } }
\NewDocumentCommand \addA { m } { \__niranjan_add_to_tmpa:n {#1} }
\NewDocumentCommand \addB { m } { \__niranjan_add_to_tmpb:n {#1} }
\cs_new:Npn \__niranjan_format_entries:nn #1#2
{ \tl_to_str:n {#1} & \tl_to_str:n {#2} \\ }
\NewDocumentCommand \listAB {}
{
\begin{tabular} { *2{>{\ttfamily}l} }
\toprule
A & B \\
\midrule
\seq_map_pairwise_function:NNN
\l_tmpa_seq \l_tmpb_seq \__niranjan_format_entries:nn
\bottomrule
\end{tabular}
}
\ExplSyntaxOff
\begin{document}
\addA {a} \addB {a}
\addA {b}
\addA {c}
\addA {d}
\addA {e}
\addA {f} \addB {f}
\listAB
\end{document}
```
Alternative methods of input for this syntax could be a key=value based input (though this puts all entries together in a single argument -- so doesn't meet your requirements "I want two separate commands for adding items to them" -- nevertheless I think the interface is pretty clean, and quite easy to implement, so here goes nothing):
```
\cs_new_protected:Npn \__niranjan_add_a_and_b_from_keyval_aux:n #1
{ \__niranjan_add_a_and_b_from_keyval_aux:nn {#1} \q_nil }
\cs_new_protected:Npn \__niranjan_add_a_and_b_from_keyval_aux:nn #1
{
\seq_put_right:Nn \l_tmpa_seq {#1}
\seq_put_right:Nn \l_tmpb_seq
}
\cs_new_protected:Npn \__niranjan_add_a_and_b_from_keyval:n
{
\keyval_parse:NNn
\__niranjan_add_a_and_b_from_keyval_aux:n
\__niranjan_add_a_and_b_from_keyval_aux:nn
}
\NewDocumentCommand \addAB { m } { \__niranjan_add_a_and_b_from_keyval:n {#1} }
\addAB {a=a}
\addAB {b}
\addAB {c}
\addAB {d,e,f=f}
```
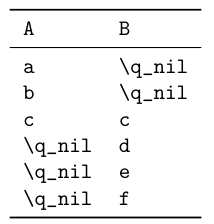
Output (regardless of whether the key=value or the first interface is used):
------
If your use case doesn't guarantee the above two constraints you could still implement something *similar* to the first variant, just with a state variable (we can't use a boolean here since there are three states, initial, A, and B -- we use an integer with the values 0, 1, and 2 for these):
```
\documentclass{article}
\usepackage{array,booktabs}
\ExplSyntaxOn
\int_new:N \l__niranjan_add_state_int
\int_zero:N \l__niranjan_add_state_int % should be implicit, but in theory might not be the case
\int_const:Nn \c__niranjan_state_A_int { 1 }
\int_const:Nn \c__niranjan_state_B_int { 2 }
\cs_new_protected:Npn \__niranjan_add_to_tmp_aux:NNNNn #1#2#3#4#5
{
% #1: seq var to be added to
% #2: state corresponding to this seq var
% #3: other seq var
% #4: state corresponding to other seq var
% #5: contents to be added
\int_compare:nNnTF \l__niranjan_add_state_int = #4
{
\seq_set_item:Nnn #1 { -1 } {#5}
\int_zero:N \l__niranjan_add_state_int
}
{
\seq_put_right:Nn #3 { \q_nil }
\seq_put_right:Nn #1 {#5}
\int_set_eq:NN \l__niranjan_add_state_int #2
}
}
\cs_new_protected:Npn \__niranjan_add_to_tmpa:n
{
\__niranjan_add_to_tmp_aux:NNNNn
\l_tmpa_seq
\c__niranjan_state_A_int
\l_tmpb_seq
\c__niranjan_state_B_int
}
\cs_new_protected:Npn \__niranjan_add_to_tmpb:n
{
\__niranjan_add_to_tmp_aux:NNNNn
\l_tmpb_seq
\c__niranjan_state_B_int
\l_tmpa_seq
\c__niranjan_state_A_int
}
\NewDocumentCommand \addA { m } { \__niranjan_add_to_tmpa:n {#1} }
\NewDocumentCommand \addB { m } { \__niranjan_add_to_tmpb:n {#1} }
\cs_new:Npn \__niranjan_format_entries:nn #1#2
{ \tl_to_str:n {#1} & \tl_to_str:n {#2} \\ }
\NewDocumentCommand \listAB {}
{
\begin{tabular} { *2{>{\ttfamily}l} }
\toprule
A & B \\
\midrule
\seq_map_pairwise_function:NNN
\l_tmpa_seq \l_tmpb_seq \__niranjan_format_entries:nn
\bottomrule
\end{tabular}
}
\ExplSyntaxOff
\begin{document}
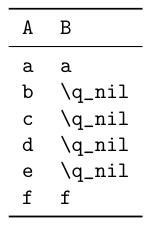
\addA {a}
\addA {b} \addB {b}
\addB {c}
\addB {d} \addA {d}
\addA {e}
\addA {f} \addB {f}
\listAB
\end{document}
```
Output:
-----
Note that `\seq_set_item:Nnn <seq-var> { -1 }` is a rather slow operation. If there was a finalising call for the setup block we could further optimise our first idea by introducing a state variable that monitors how many items overhead are already built up (this is close to your code, but a bit faster by simply counting the number of items while we go, instead of every time we add to `b`):
```
\documentclass{article}
\usepackage{array,booktabs}
\ExplSyntaxOn
\int_new:N \l__niranjan_A_overhead_int
\int_zero:N \l__niranjan_A_overhead_int % should be implicit, but in theory might not be the case
\cs_new_protected:Npn \__niranjan_add_to_tmpa:n
{
\int_incr:N \l__niranjan_A_overhead_int
\seq_put_right:Nn \l_tmpa_seq
}
\cs_new_protected:Npn \__niranjan_add_to_tmpb:n
{
\__niranjan_balance_seqs:
\seq_put_right:Nn \l_tmpb_seq
}
\cs_new_protected:Npn \__niranjan_balance_or_finalise:n #1
{
\prg_replicate:nn {#1}
{ \seq_put_right:Nn \l_tmpb_seq { \q_nil } }
\int_zero:N \l__niranjan_A_overhead_int
}
\cs_new_protected:Npn \__niranjan_balance_seqs:
{ \__niranjan_balance_or_finalise:n { \l__niranjan_A_overhead_int - 1 } }
\cs_new_protected:Npn \__niranjan_finalise:
{ \__niranjan_balance_or_finalise:n \l__niranjan_A_overhead_int }
\NewDocumentCommand \addA { m } { \__niranjan_add_to_tmpa:n {#1} }
\NewDocumentCommand \addB { m } { \__niranjan_add_to_tmpb:n {#1} }
\NewDocumentCommand \doneAdding {} { \__niranjan_finalise: }
\cs_new:Npn \__niranjan_format_entries:nn #1#2
{ \tl_to_str:n {#1} & \tl_to_str:n {#2} \\ }
\NewDocumentCommand \listAB {}
{
\begin{tabular} { *2{>{\ttfamily}l} }
\toprule
A & B \\
\midrule
\seq_map_pairwise_function:NNN
\l_tmpa_seq \l_tmpb_seq \__niranjan_format_entries:nn
\bottomrule
\end{tabular}
}
\ExplSyntaxOff
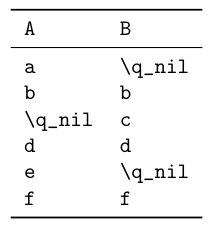
\begin{document}
\addA {a} \addB {a}
\addA {b}
\addA {c}
\addA {d}
\addA {e}
\addA {f}
\doneAdding
\listAB
\end{document}
```
----
Lastly, we can reintroduce the constraint that we don't know which sequence is added first and which second, and which one contains more items. For that we use positive values to indicate an overhead of A, and negative ones to indicate an overhead of B:
```
\documentclass{article}
\usepackage{array,booktabs}
\ExplSyntaxOn
\int_new:N \l__niranjan_imbalance_int
\int_zero:N \l__niranjan_imbalance_int % should be implicit, but in theory might not be the case
\cs_new_protected:Npn \__niranjan_add_to_tmpa:n
{
\__niranjan_balance_seqs:NN < \l_tmpa_seq
\int_incr:N \l__niranjan_imbalance_int
\seq_put_right:Nn \l_tmpa_seq
}
\cs_new_protected:Npn \__niranjan_add_to_tmpb:n
{
\__niranjan_balance_seqs:NN > \l_tmpb_seq
\int_decr:N \l__niranjan_imbalance_int
\seq_put_right:Nn \l_tmpb_seq
}
\cs_new_protected:Npn \__niranjan_balance_seqs:NN #1#2
{
\int_compare:nNnT \l__niranjan_imbalance_int #1 \c_zero_int
{
\prg_replicate:nn { \int_abs:n \l__niranjan_imbalance_int - 1 }
{ \seq_put_right:Nn #2 { \q_nil } }
\int_zero:N \l__niranjan_imbalance_int
}
}
\cs_new_protected:Npn \__niranjan_finalise:
{
\int_compare:nNnTF \l__niranjan_imbalance_int > \c_zero_int
{
\prg_replicate:nn \l__niranjan_imbalance_int
{ \seq_put_right:Nn \l_tmpb_seq { \q_nil } }
}
{
\prg_replicate:nn { - \l__niranjan_imbalance_int }
{ \seq_put_right:Nn \l_tmpa_seq { \q_nil } }
}
\int_zero:N \l__niranjan_imbalance_int
}
\NewDocumentCommand \addA { m } { \__niranjan_add_to_tmpa:n {#1} }
\NewDocumentCommand \addB { m } { \__niranjan_add_to_tmpb:n {#1} }
\NewDocumentCommand \doneAdding {} { \__niranjan_finalise: }
\cs_new:Npn \__niranjan_format_entries:nn #1#2
{ \tl_to_str:n {#1} & \tl_to_str:n {#2} \\ }
\NewDocumentCommand \listAB {}
{
\begin{tabular} { *2{>{\ttfamily}l} }
\toprule
A & B \\
\midrule
\seq_map_pairwise_function:NNN
\l_tmpa_seq \l_tmpb_seq \__niranjan_format_entries:nn
\bottomrule
\end{tabular}
}
\ExplSyntaxOff
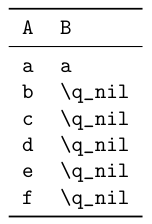
\begin{document}
\addA {a}
\addA {b}
\addA {c} \addB {c}
\addB {d}
\addB {e}
\addB {f}
\doneAdding
\listAB
\end{document}
```