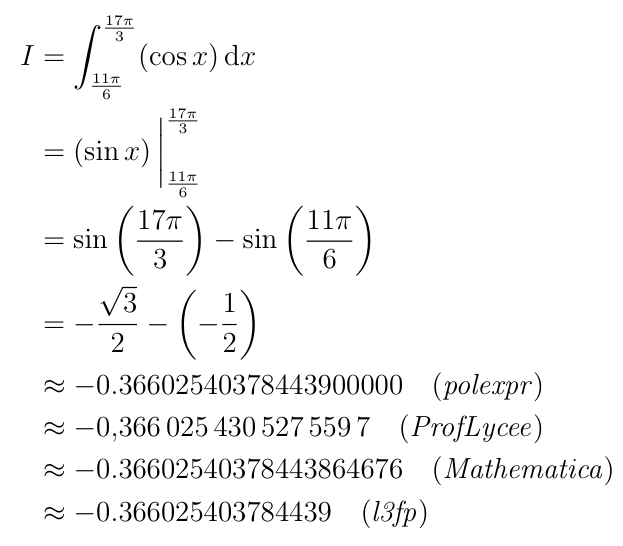JohnPaul

This is my code
```
\renewcommand{\mya}{pi/6}
\renewcommand{\myb}{pi/3}
\def\myda{\pi/6}
\def\mydb{\pi/3}
```
How can I defintion `\myda' by using `\mya? in this code?
```
\documentclass[12pt,a4paper]{article}
\usepackage{polexpr}
\usepackage[xcolor]{ProfLycee}
\usepackage{amsmath}
\begin{document}
\def\mya{11pi/6}
\def\myb{17pi/3}
\def\myda{\frac{11\pi}{6}}
\def\mydb{\frac{17\pi}{3}}
\def\mydaa{11*Pi/6}
\def\mydbb{17*Pi/3}
\xintdeffunc f(x):= sin(x);
\begin{align*}
I &= \int_{\myda}^{\mydb}(\cos x)\,\mathrm{d}x \\
&= \left(\sin x\right)\bigg|_{\myda}^{\mydb} \\
&= \sin \left(\mydb\right)- \sin \left(\myda\right) \\
&=\LigneTrigo[d]{sin}(\myb)-\left(\LigneTrigo[d]{sin}(\mya)\right)\\
&\approx\xintRound{20}{\xinteval{f(\mydbb)-f(\mydaa)}} \quad \text{(\textit{polexpr})}\\
&\approx\CalcIntegrale*<100>{sin(x)}{\mydbb}{\mydaa} \quad \text{(\textit{ProfLycee})}\\
&\approx-0.36602540378443864676 \quad \text{(\textit{Mathematica})}
\end{align*}
\end{document}
```
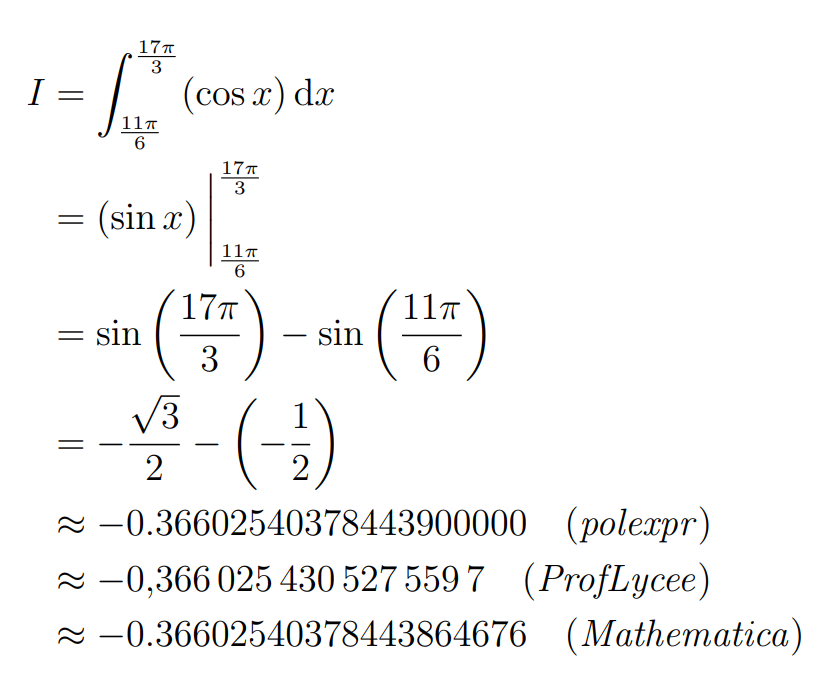
Top Answer
Skillmon

If it's just about parsing `<num1>pi/<num2>` into `\frac{<num1>\pi}{<num2>}` the easiest (but rather slow) solution would be to use `l3regex`.
Also please note that you don't need a package to calculate floating point numbers, `l3fp` is part of the kernel and has decent precision (and understands your `\mya` and `\myb` just fine).
```
\documentclass[12pt,a4paper]{article}
\usepackage{polexpr}
\usepackage[xcolor]{ProfLycee}
\usepackage{amsmath}
\ExplSyntaxOn
\tl_new:N \l_JohnPaul_tmp_tl
\NewDocumentCommand\formatpifrac{m}
{
\tl_set:Nn \l_JohnPaul_tmp_tl {#1}
\regex_replace_all:nnN
{ (\d+)pi/(\d+) } { \c{frac}{\1\c{pi}}{\2} } \l_JohnPaul_tmp_tl
\l_JohnPaul_tmp_tl
}
\ExplSyntaxOff
\begin{document}
\def\mya{11pi/6}
\def\myb{17pi/3}
\def\myda{\ExpandArgs{V}\formatpifrac\mya}
\def\mydb{\ExpandArgs{V}\formatpifrac\myb}
\def\mydaa{11*Pi/6}
\def\mydbb{17*Pi/3}
\xintdeffunc f(x):= sin(x);
\begin{align*}
I &= \int_{\myda}^{\mydb}(\cos x)\,\mathrm{d}x \\
&= \left(\sin x\right)\bigg|_{\myda}^{\mydb} \\
&= \sin \left(\mydb\right)- \sin \left(\myda\right) \\
&=\LigneTrigo[d]{sin}(\myb)-\left(\LigneTrigo[d]{sin}(\mya)\right)\\
&\approx\xintRound{20}{\xinteval{f(\mydbb)-f(\mydaa)}} \quad \text{(\textit{polexpr})}\\
&\approx\CalcIntegrale*<100>{sin(x)}{\mydbb}{\mydaa} \quad \text{(\textit{ProfLycee})}\\
&\approx-0.36602540378443864676 \quad \text{(\textit{Mathematica})} \\
&\approx\fpeval{sin(\myb)-sin(\mya)} \quad\text{(\textit{l3fp})}
\end{align*}
\end{document}
```
------
In the code above `l3regex` ran multiple times (each time you call `\myda` or `\mydb`). We could speed this up by directly defining macros with it that store the result:
```
\documentclass[12pt,a4paper]{article}
\usepackage{polexpr}
\usepackage[xcolor]{ProfLycee}
\usepackage{amsmath}
\ExplSyntaxOn
\tl_new:N \l_JohnPaul_tmp_tl
\NewDocumentCommand\formatpifrac{m m}
{
\tl_set:Nn \l_JohnPaul_tmp_tl {#2}
\regex_replace_all:nnN
{ (\d+)pi/(\d+) } { \c{frac}{\1\c{pi}}{\2} } \l_JohnPaul_tmp_tl
\tl_set_eq:NN #1 \l_JohnPaul_tmp_tl
}
\ExplSyntaxOff
\begin{document}
\def\mya{11pi/6}
\def\myb{17pi/3}
\ExpandArgs{nV}\formatpifrac\myda\mya
\ExpandArgs{nV}\formatpifrac\mydb\myb
\def\mydaa{11*Pi/6}
\def\mydbb{17*Pi/3}
\xintdeffunc f(x):= sin(x);
\begin{align*}
I &= \int_{\myda}^{\mydb}(\cos x)\,\mathrm{d}x \\
&= \left(\sin x\right)\bigg|_{\myda}^{\mydb} \\
&= \sin \left(\mydb\right)- \sin \left(\myda\right) \\
&=\LigneTrigo[d]{sin}(\myb)-\left(\LigneTrigo[d]{sin}(\mya)\right)\\
&\approx\xintRound{20}{\xinteval{f(\mydbb)-f(\mydaa)}} \quad \text{(\textit{polexpr})}\\
&\approx\CalcIntegrale*<100>{sin(x)}{\mydbb}{\mydaa} \quad \text{(\textit{ProfLycee})}\\
&\approx-0.36602540378443864676 \quad \text{(\textit{Mathematica})} \\
&\approx\fpeval{sin(\myb)-sin(\mya)} \quad\text{(\textit{l3fp})}
\end{align*}
\end{document}
```
------
Result of both: