I know that, the function $f(x) = (3*x^2+2*x+7)/(3*x+5)$ has two extrapoints are $(-11/3, -20/3)$ and $(1/3,4/3)$. 
I use [this answers](https://topanswers.xyz/tex?q=7794) ans tried

```
\documentclass[12pt,a4paper]{article}
\usepackage[left=2cm, right=2cm, top=2cm, bottom=2cm]{geometry}
\usepackage{fouriernc} 
\usepackage{pgfplots} 
\pgfplotsset{compat=1.18
}
\usepackage{float}
\usepackage{amsmath}
\usepackage{amsthm}
\begin{document} 
\begin{figure}[H]
		\centering
\begin{tikzpicture}[>=stealth,scale =1,declare function={a=3;b=2;c=7;d=3;k=5; 
f(\x)=(a*\x*\x+b*\x+c)/(d*\x+k); 
g(\x)=b/d - (a* k)/d^2 + (a *\x)/d; 
x1=(-a* k - sqrt(a*c*d^2 - a *b* d* k + a^2* k^2))/(a* d); 
x2=(-a*k + sqrt(a*c*d^2 - a*b* d*k + a^2* k^2))/(a*d);  
xmin=-7;xmax=5;ymin=-8;ymax=3;}] 
\draw[gray!30] (xmin,ymin) grid (xmax,ymax); 
\draw[->, thick] (xmin,0)--(xmax,0) node [below left]{$x$};
\draw[->,thick] (0,ymin)--(0,ymax) node [below right]{$y$};
\foreach \X in {x1,x2} {\draw[dashed] (\X,0) |- (0,{f(\X)}); } 
\node[below right] at (0, 0) {$O$}; 
\foreach \Y in {x1,x2,0} \fill (\Y,{f(\Y)}) circle(2pt); 

\foreach \p/\g [evaluate=\p] in {x1/90,x2/180}{%
  \draw(\p,0)node[shift={(\g:.3)}]{$\p$};
}
\foreach \p/\g in {x1/0,x2/180}{%
\pgfmathparse{f(\p)}
\draw(0,\pgfmathresult)node[shift={(\g:.5)}]{$\fpeval{round(\pgfmathresult,2)}$};
}
 
\clip (xmin,ymin) rectangle (xmax,ymax);
			
\draw[smooth,samples=500,very thick, blue,domain=xmin:10.9] plot(\x,{f(\x)});
				
\draw[smooth,samples=500,very thick, blue,domain=11.1:xmax] plot(\x,{f(\x)});	
			
\draw[smooth,samples=500,very thick, blue,domain=xmin:xmax]plot(\x,{g(\x)});
		
\draw[thick, blue] (-k/d,ymin) -- (-k/d,ymax);
\fill[red] (-k/d,{-((-b* d + 2 *a *k)/d^2)}) circle(2 pt); 
\end{tikzpicture} 
\end{figure}
	
\end{document} 
```

and got

![image.png](/image?hash=2c13724fe4e98a7e23f87e156839e8a303273f8f0fb110f1328db0a79c2fd6c6)

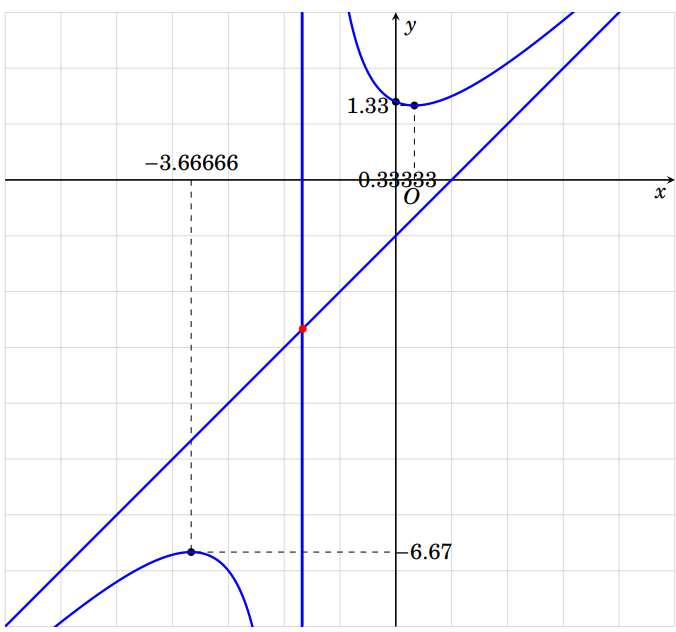
How can I chang the numbers `-6.67` into `-20/3`, `-3.66666` into `-11/3`, `0.33333` into `1/3` and `1.33` into `4/3`.

Can I use this answer to my question?

[here](https://tex.stackexchange.com/questions/722475/how-can-i-get-f2-3-20-9-and-f4-3-16-9-of-the-function-fx-3-x3/722615#722615)

```
\documentclass[12pt,a4paper]{article}
\usepackage{pgfplots} 
 \usepackage{xintexpr}
\ExplSyntaxOn

\bool_new:N \l__pgfmathxintexpr_xinteval_bool

\tl_new:N \l__pgfmathxintexpr_function_tl
\tl_new:N \l__pgfmathxintexpr_parse_tl

\cs_new_eq:NN \__pgfmathxintexpr_pgfmath_parse_old:n \pgfmathparse

\cs_new_eq:NN \__pgfmathxintexpr_pgfmath_print_number_old:wn \pgfmathprintnumber

\pgfkeys
  {
    / pgf / declare~xintexpr~function /. code =
      {
        \tikzset { declare~function = { #1 ; } }
        \tl_set:Nn \l__pgfmathxintexpr_function_tl { #1 ) ; }
        \tl_replace_all:Nnn \l__pgfmathxintexpr_function_tl { \x } { x }
        \tl_replace_once:Nnn \l__pgfmathxintexpr_function_tl { = } { : = reduce ( }
        \exp_after:wN \xintdeffunc \l__pgfmathxintexpr_function_tl
      } ,
    / pgf / number~format / xintexpr /. code = \bool_set:Nn \l__pgfmathxintexpr_xinteval_bool { \cs:w c_#1_bool\cs_end: } ,
    / pgf / number~format / xintexpr /. default = true ,
    / pgf / number~format / xintexpr = false
  }

\RenewDocumentCommand \pgfmathparse { m }
  {
    \__pgfmathxintexpr_pgfmath_parse_old:n {#1}
    \tl_set:Nn \l__pgfmathxintexpr_parse_tl {#1}
  }

\RenewDocumentCommand \pgfmathprintnumber { O {} m }
  {
    {
      \pgfkeys { / pgf / number~format , #1 }
      \bool_if:NTF \l__pgfmathxintexpr_xinteval_bool
        {
          \tl_if_eq:nnTF {#2} { \pgfmathresult }
            { \xinteval { \l__pgfmathxintexpr_parse_tl } }
            { \xinteval {#2} }
        }
        { \__pgfmathxintexpr_pgfmath_print_number_old:wn [#1] {#2} }
    }
  }

\ExplSyntaxOff


\begin{document}
\begin{tikzpicture}[declare xintexpr function={f(\x)=(3*\x*\x+2*\x+7)/(3*\x+5)}] \node at (0,0) {\pgfmathprintnumber[xintexpr]{f(1/3)}}; 
\node at (0,-1) {$\pgfmathprintnumber[xintexpr]{f(-11/3)}$};
\end{tikzpicture}
 \end{document} 
 
```