Trevor

In MetaPost, I would like to fill in the region in between non-intersecting shapes with a color, similar to how a "bucket fill" tool works in an image editing program. Consider the following code:
```
beginfig(1);
path a,b,c;
a = fullcircle scaled 200;
b = fullcircle scaled 70 shifted (40,40);
c = fullcircle scaled 40 shifted (-20,20);
draw a;
draw b;
draw c;
endfig;
```
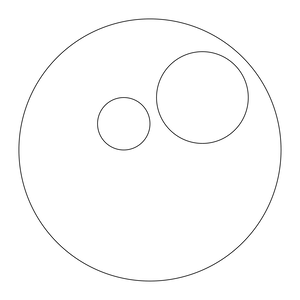
From this code, I would like to produce this:

I have tried using the `unfill` command (i.e., `fill a; unfill b; unfill c;`), but that command makes the smaller circles white rather than transparent. So if I open the image using a graphics editor program which shows transparency as a checkerboard pattern, I get this:

I have also tried doing `fill a--reverse b--reverse c--cycle;` but that also does not make the negative space transparent, and also does not render the shapes properly because of how the paths are connected.
**How do I make this figure in a way so that the smaller circles are transparent?**
Top Answer
frougon

The problem has been addressed [in the comments section](https://topanswers.xyz/transcript?room=7411&id=174834#c174834) for the particular circles whose code was provided in the question.
It was subsequently [asked](https://topanswers.xyz/transcript?room=7411&id=174850#c174850) if there is a method that would work for, say, 100 holes cut into the large disc. Extending the trick used for two holes to a large number of holes doesn't seem straightforward nor elegant, and I can't see another way with MetaPost—which does not mean there is none. Therefore, I propose TikZ/expl3 code that does the job for an arbitrary number of circles (precisely 100 in the given example, but it is all parametrized).

The main function is `\computeHoleLocations`; it accepts the following parameters (a key-value interface would clearly be more convenient, but this is not the point of the exercise):
```
#1: node name for the center of the enclosing disc
#2: radius of the enclosing disc, in the xy-coordinate system
#3: minimum hole radius
#4: maximum hole radius
#5: number of holes
#6: minimum distance between holes, in the xy-coordinate system
#7: minimum distance between a hole and the outer circle, in the
xy-coordinate system
```
Any two holes are guaranteed to have at least #6 of space between them. Any hole is guaranteed to lie at least #7 from the border of the background disc.
(If you ask for something difficult or just impossible, TeX will try very hard; compilation may take a long time in such cases!)
```
\documentclass[tikz,border=2mm]{standalone}
\makeatletter
\ExplSyntaxOn
\seq_new:N \l__my_centers_seq % {x1}{y1}, {x2}{y2}, ... with unit
\seq_new:N \l__my_radii_seq % each element has the unit explicitly included
\dim_new:N \l__my_xunit_dim
% For parameters used by callees
\tl_new:N \l__my_disc_center_tl % a \pgfpoint
\tl_new:N \l__my_disc_radius_tl
\tl_new:N \l__my_min_hole_radius_tl
\tl_new:N \l__my_max_hole_radius_tl
\tl_new:N \l__my_min_dist_between_holes_tl
\tl_new:N \l__my_min_dist_from_outer_circle_tl
% #1: node name for the center of the enclosing disc
% #2: radius of the enclosing disc, in the xy-coordinate system
% #3: minimum hole radius
% #4: maximum hole radius
% #5: number of holes
% #6: minimum distance between holes, in the xy-coordinate system
% #7: minimum distance between a hole and the outer circle, in the
% xy-coordinate system
\cs_new_protected:Npn \my_compute_hole_locations:nnnnnnn #1#2#3#4#5#6#7
{
% Extract the length of the first vector (arbitrary choice) of the
% xy-coordinate system.
\pgfextractx { \l__my_xunit_dim } { \pgfpointxy { 1 } { 0 } }
\seq_clear:N \l__my_centers_seq
\seq_clear:N \l__my_radii_seq
\pgf@process { \pgfpointanchor {#1} { center } }
\tl_set:Ne \l__my_disc_center_tl
{ \exp_not:N \pgfpoint { \the\pgf@x } { \the\pgf@y } }
\pgfmathsetmacro { \l__my_disc_radius_tl } {#2}
\pgfmathsetmacro { \l__my_min_hole_radius_tl } {#3}
\pgfmathsetmacro { \l__my_max_hole_radius_tl } {#4}
\pgfmathsetlengthmacro { \l__my_min_dist_between_holes_tl }
{ (#6) * \l__my_xunit_dim }
\pgfmathsetmacro { \l__my_min_dist_from_outer_circle_tl } {#7}
\prg_replicate:nn {#5} { \__my_add_hole: }
}
\dim_new:N \l__my_cand_center_x_dim
\dim_new:N \l__my_cand_center_y_dim
\tl_new:N \l__my_cand_radius_tl % in pt
\tl_new:N \l__my_cand_radius_xy_tl % in units of the xy-coordinate system
\bool_new:N \l__my_hole_was_added_bool
\cs_new_protected:Npn \__my_add_hole:
{
\bool_set_false:N \l__my_hole_was_added_bool
\bool_do_until:Nn \l__my_hole_was_added_bool
{
\__my_try_candidate_hole:
{ % This part is only executed when the candidate was far enough from
% all already determined holes.
\seq_put_right:Ne \l__my_centers_seq
{
{ \dim_use:N \l__my_cand_center_x_dim }
{ \dim_use:N \l__my_cand_center_y_dim }
}
\seq_put_right:NV \l__my_radii_seq \l__my_cand_radius_tl
\bool_set_true:N \l__my_hole_was_added_bool
}
}
}
% Vector between the centers of two circles
\tl_new:N \l__my_vec_x_tl
\tl_new:N \l__my_vec_y_tl
\cs_new_protected:Npn \__my_try_candidate_hole:
{
% Pick a random radius
\pgfmathsetmacro { \l__my_cand_radius_xy_tl }
{
\l__my_min_hole_radius_tl +
rnd * ( \l__my_max_hole_radius_tl - \l__my_min_hole_radius_tl )
}
\pgfmathsetlengthmacro { \l__my_cand_radius_tl }
{ \l__my_cand_radius_xy_tl \l__my_xunit_dim }
% Pick a random center location, just far enough from the outer circle
\pgfpointadd { \l__my_disc_center_tl }
{
\pgfpointpolarxy { rnd*360 }
{
rnd * ( \l__my_disc_radius_tl - \l__my_cand_radius_xy_tl -
\l__my_min_dist_from_outer_circle_tl )
}
}
% Save it
\dim_set_eq:NN \l__my_cand_center_x_dim \pgf@x
\dim_set_eq:NN \l__my_cand_center_y_dim \pgf@y
% Check distance from all holes that have been retained so far
\seq_map_indexed_inline:Nn \l__my_centers_seq
{
\__my_candidate_if_too_close_to_other_hole:nnT {##1} {##2}
{ \seq_map_break:n { \use_none:nn } } % candidate rejected
}
\use:n % accepted!
}
\prg_new_protected_conditional:Npnn
\__my_candidate_if_too_close_to_other_hole:nn #1#2 { T }
{
\pgfpointdiff
{ \pgfpoint { \l__my_cand_center_x_dim } { \l__my_cand_center_y_dim } }
{ \pgfpoint #2 }
\pgfgetlastxy { \l__my_vec_x_tl } { \l__my_vec_y_tl }
% Are the two circles too close to each other?
\pgfmathless { veclen(\l__my_vec_x_tl, \l__my_vec_y_tl) }
{
\seq_item:Nn \l__my_radii_seq {#1} + \l__my_cand_radius_tl +
\l__my_min_dist_between_holes_tl
}
\int_compare:nNnTF { \pgfmathresult } = { 1 }
{ \prg_return_true: }
{ \prg_return_false: }
}
\cs_new:Npn \__my_hole_center:nn #1#2 { (#1,#2) }
% Write TikZ code for all holes defined by \l__my_centers_seq and
% \l__my_radii_seq to the specified tl var.
%
% #1: tl var
\cs_new_protected:Npn \my_set_to_tikz_code_for_holes:N #1
{
\cs_set_protected:Npn \__my_append_tikz_code_for_one_hole:nn ##1##2
{
\tl_put_right:No #1 { \__my_hole_center:nn ##1~ circle[radius=##2]~ }
}
\tl_clear:N #1
% Append TikZ code for all holes defined by these sequence variables
\seq_map_pairwise_function:NNN \l__my_centers_seq \l__my_radii_seq
\__my_append_tikz_code_for_one_hole:nn
}
\tl_new:N \l__my_ihcit_tikz_code_tl
\cs_new_protected:Npn \__my_ihcit_tmp_func:n #1 { }
\cs_generate_variant:Nn \__my_ihcit_tmp_func:n { V }
% Use the provided template, replacing #1 in it with the TikZ code for all
% holes.
%
% #1: template
\cs_new_protected:Npn \my_insert_holes_code_in_template:n #1
{
\my_set_to_tikz_code_for_holes:N \l__my_ihcit_tikz_code_tl
\cs_set_protected:Npn \__my_ihcit_tmp_func:n ##1 {#1}
\__my_ihcit_tmp_func:V \l__my_ihcit_tikz_code_tl
}
\cs_new_eq:NN \computeHoleLocations \my_compute_hole_locations:nnnnnnn
\cs_new_eq:NN \insertHolesCodeInTemplate \my_insert_holes_code_in_template:n
\ExplSyntaxOff
\makeatother
\newdimen\myXUnit
%\pgfmathsetseed{12} % if you want to control the pseudo-RNG
\begin{document}
\begin{tikzpicture}
\pgfextractx{\myXUnit}{\pgfpointxy{1}{0}}
\def\myDiscRadius{9}
\def\myNbHoles{100}
\coordinate (O) at (2,3);
\computeHoleLocations{O}{\myDiscRadius}{0.08}{2.9}{\myNbHoles}{0.3}{0.3}
% This replaces #1 with TikZ code for all holes
\insertHolesCodeInTemplate{
\fill[black, even odd rule] (O) circle[radius=\myDiscRadius\myXUnit] #1;
}
\end{tikzpicture}
\end{document}
```