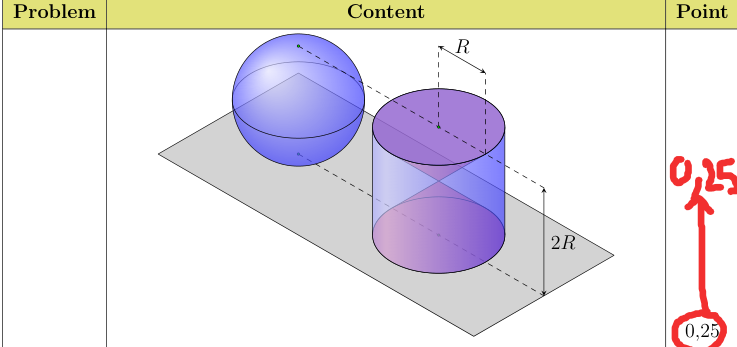There are two unrelated problems:

- you can use the `baseline` option to change the vertical alignment of the tikzpicture with respect to the surrounding text

- to avoid the merged cells to spill over the bottom of the page, you can use `\nopagebreak` to avoid page breaks in the rows which share a merged cell (might result in a lot of white space as you cells are very large)

```
\documentclass[12pt]{article}
\usepackage{tabularray}
\usepackage[utf8]{vietnam}
\UseTblrLibrary{diagbox}
\UseTblrLibrary{varwidth}
\UseTblrLibrary{booktabs}
\UseTblrLibrary{counter}
\usepackage{enumitem}
\usepackage{ninecolors}
\UseTblrLibrary{amsmath}
%\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{siunitx}
\sisetup{output-decimal-marker={,}}
\UseTblrLibrary{siunitx} 
\usepackage{tikz}
\usetikzlibrary{3d}         % 'canvas is...' options
\usetikzlibrary{perspective} % isometric view

% isometric axes
\pgfmathsetmacro\xx{1/sqrt(2)}
\pgfmathsetmacro\xy{1/sqrt(6)}
\pgfmathsetmacro\zz{sqrt(2/3)}

\def\r{2} % radius

\pgfdeclareradialshading{rblue}{\pgfpoint{-0.4cm}{0.4cm}}
{% shading, sphere
	color(0cm)=(blue!10);
	color(1cm)=(blue!80)
}

\pgfdeclarehorizontalshading{hblue}{100pt}
{% shading, cylinder
	color(0pt)=(blue!80);
	color(30pt)=(blue!20);
	color(100pt)=(blue!100)
}

% styles
\tikzset%
{%
	isometric/.style={x={(-\xx cm,-\xy cm)},y={(\xx cm,-\xy cm)},z={(0cm,\zz cm)}},
	plane/.style={fill=gray,fill opacity=0.4},
	sphere/.style={shading=rblue,fill opacity=0.7},
	cylinder surface/.style={shading=hblue,fill opacity=0.7},
	cylinder base/.style={fill=blue!50,fill opacity=0.7},
	cone/.style={fill=red,fill opacity=0.5}
}
\usepackage[paperwidth=19cm, paperheight=26.5cm, left=1.7cm,right=1.7cm,top=1.8cm,bottom=1.7cm]{geometry}
\DefTblrTemplate{contfoot-text}{normal}{Continued on next page}
\SetTblrTemplate{contfoot-text}{normal}
\DefTblrTemplate{conthead-text}{normal}{(Continued)}
\SetTblrTemplate{conthead-text}{normal}
\SetTblrTemplate{conthead-text}{normal}
\newcounter{mycnta}
\newcommand{\mycnta}{\stepcounter{mycnta}\arabic{mycnta}}


\newcommand{\startproblem}[1]{
	\SetCell[r=#1]{m}\SetRow{bg=teal9}\SetCell{bg=gray9}\mycnta
}

\begin{document}
	

	\begin{longtblr}[
		expand=\startproblem,
		caption={Some text}]{
		colspec = {Q[c,gray9]X[l,valign=m]Q[c]},
			rowhead = 1,
			vlines,
			hlines,
			row{1}={yellow9,font=\bfseries},
			cell{1}{2-3}={halign=c},
			column{1}={font=\bfseries},
		}
		Problem & Content & Point \\
		\startproblem{5}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\startproblem{4}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ $ y = \dfrac{2x+1}{x-2} $ $ y = \dfrac{2x+1}{x-2} $ $ y = \dfrac{2x+1}{x-2} $ $ y = \dfrac{2x+1}{x-2} $ $ y = \dfrac{2x+1}{x-2} $&  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\startproblem{3}	& Is this $ x^2 + 3x +4 >0$ true or fail? why?  &  \num{0.75}  \\\nopagebreak
		&  $ x^2 + 3x +4 >0$ true. & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}
		\\
		\startproblem{5}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\startproblem{4}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ &  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\startproblem{3}	& Is this $ x^2 + 3x +4 >0$ true or fail? why?  &  \num{0.75}  \\\nopagebreak
		&  $ x^2 + 3x +4 >0$ true. & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}
		\\
		\startproblem{5}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\startproblem{4}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ &  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\startproblem{3}	&\SetCell{c}
			\begin{tikzpicture}[isometric view,rotate=-20,baseline]
			% sphere, inner
			\foreach\i in {3,2,1}
			\draw[canvas is yz plane at x=0,top color=red!70] (0,0) circle (\i);
			% sphere, outer
			\foreach\i in {1,2,3}
			\draw[shading=ball,ball color=red!70] (120:\i cm) arc (120:-60:\i cm)
			{[canvas is yz plane at x=0] arc (225: 45:\i)};
			% rays
			\foreach\i in {0,60,120}
			\draw[canvas is yz plane at x=0,blue!70!black,ultra thick,latex-latex]
			(\i:4.5) -- (\i+180:4.5);
			\draw[shading=ball,ball color=blue!30] (0,0) circle (0.25cm);
		\end{tikzpicture} &  \num{0.75}  \\\nopagebreak
		& 
		\SetCell{c} \begin{tikzpicture}[isometric,line cap=round,line join=round,scale=.7,baseline]
			% plane and points
			\draw[plane] (-3,-9,-2) -- (-3,4.5,-2) -- (3,4.5,-2) -- (3,-9,-2) -- cycle;
			\draw[dashed] (0,-6,-2) -- (0,4.5,-2);
			\foreach\y in {-6,0}
			\draw[fill=green] (0,\y,-2) circle (1pt);
			% sphere
			\draw         (0,-6,0) ++ (315:2) arc (315:135:2);
			\draw[sphere] (0,-6,0) circle (2cm);
			\draw         (0,-6,0) ++ (-45:2) arc (-45:135:2);
			% cone
			\draw[cone] (2,0,2) arc (0:90:\r) -- (0,-2,-2) arc (-90:180:2) -- cycle;
			\draw[cone] (0,0,2) circle (2);
			% cylinder
			\draw (0,0,-2) ++ (315:2) arc (315:135:2);
			\draw[cylinder surface] (0,0,-2) ++ (-45:2) arc (-45:135:2) --++ (0,0,4) arc (135:-45:2) -- cycle;
			\draw[cylinder base] (0,0,2) circle (2);
			% lines and points
			\draw[dashed] (0,-6,2) -- (0,4.5,2);
			\foreach\y in {0,2}
			\draw[dashed] (0,\y,2) -- (0,\y,5);
			\draw[stealth-stealth] (0,4.5,2) -- (0,4.5,-2) node [midway,right] {$2R$};
			\draw[stealth-stealth] (0,0,5) -- (0,2,5) node [midway,above] {$R$};
			\foreach\y in {-6,0}
			\draw[fill=green] (0,\y,2) circle (1pt);
		\end{tikzpicture} & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}\\
	\startproblem{4}	& 	Solve the equation
	$(2 x+3)\cdot \sqrt{4 x+5}+(6 x+7) \cdot\sqrt{8 x+9}=2. $
		&  \num{0.75}  \\
	& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
	& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
	& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\	
	\end{longtblr} 

\end{document}
```
![Screenshot 2023-02-16 at 12.16.04.png](/image?hash=49aa266827e3fddb3ad3a60db4ddec6fbade6c44960c24d8e4823d81f504336e)