I have long table. 
```
\documentclass[12pt]{article}
\usepackage{tabularray}
\UseTblrLibrary{diagbox}
\UseTblrLibrary{varwidth}
\UseTblrLibrary{booktabs}
\UseTblrLibrary{counter}
\usepackage{enumitem}
\usepackage{ninecolors}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{siunitx}
\sisetup{output-decimal-marker={,}}
\UseTblrLibrary{siunitx} 
\usepackage[paperwidth=19cm, paperheight=26.5cm, left=1.7cm,right=1.7cm,top=1.8cm,bottom=1.7cm]{geometry}
\DefTblrTemplate{contfoot-text}{normal}{Continued on next page}
\SetTblrTemplate{contfoot-text}{normal}
\DefTblrTemplate{conthead-text}{normal}{(Continued)}
\SetTblrTemplate{conthead-text}{normal}
\SetTblrTemplate{conthead-text}{normal}
\newcounter{mycnta}
\newcommand{\mycnta}{\stepcounter{mycnta}\arabic{mycnta}}
\begin{document}
	\begin{longtblr}[
		caption={Some text}]{
			colspec = {Q[c,gray9]X[l]Q[c]},
			vlines,
			hlines,
row{1}={yellow9,font=\bfseries},
cell{2,7,11}{2-3} ={teal9},
%cell{7}{2-3} ={teal9},
%cell{11}{2-3} ={teal9},
hline{1,2,Y,Z} = {solid},
cell{1}{2-3}={halign=c},
column{1}={font=\bfseries},
cell{2-Z}{1}={cmd={\mycnta}},}
Problem & Content & Point \\
\SetCell[r=5]{m}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\SetCell[r=4]{m}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ &  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\SetCell[r=3]{m}	& Is this $ x^2 + 3x +4 >0$ true or fail? why?  &  \num{0.75}  \\
		&  $ x^2 + 3x +4 >0$ true. & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}
		\\
		\SetCell[r=5]{m}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\SetCell[r=4]{m}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ &  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\SetCell[r=3]{m}	& Is this $ x^2 + 3x +4 >0$ true or fail? why?  &  \num{0.75}  \\
		&  $ x^2 + 3x +4 >0$ true. & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}
		\\
		\SetCell[r=5]{m}	& Solve the equation $ x^2 - 5x + 6 = 0 $ &  \num{1.00}   \\
		& $ \Delta =(-5)^2 - 4 \cdot 1 \cdot 6 = 1$, & \num{0.25} \\
		& $ x = \dfrac{-(-5) -1}{2} = 2$. & \num{0.25} \\
		& $ x = \dfrac{-(-5)  + 1}{2} = 3$ & \num{0.25} \\
		& The given equation has two solutions $x=2$ and $x = 3$. & \num{0.25} \\
		\SetCell[r=4]{m}	& Find the derivaty of the function $ y = \dfrac{2x+1}{x-2} $ &  \num{0.75}  \\
		& $ y' = \dfrac{(2x+1)'(x-2)-(2x+1)(x-2)'}{(x-2)^2}$. & \num{0.25} \\
		& $ y'=\dfrac{2(x-2) -(2x+1)}{(x-2)^2}$. & \num{0.25} \\
		& $y'=-\dfrac{5}{(x-2)^2}$. & \num{0,25} \\
		\SetCell[r=3]{m}	& Is this $ x^2 + 3x +4 >0$ true or fail? why?  &  \num{0.75}  \\
		&  $ x^2 + 3x +4 >0$ true. & \num{0.25} \\
		& $ x^2 + 3x +4 $ have $ \Delta = -7<0 $ and coefficient of  $ x^2 $ is $ 1 >0$. & \num{0.50}
	\end{longtblr} 
\end{document}
```
![image.png](/image?hash=4bcaedca6c5984b1242a3b575795f635c0d14739a4fbf7bed22d6e510fb0baf7)

![image.png](/image?hash=f8a4f1757cda3ad909d90fbccaeeb04797f7351b970e18421d4d27b59057b395)
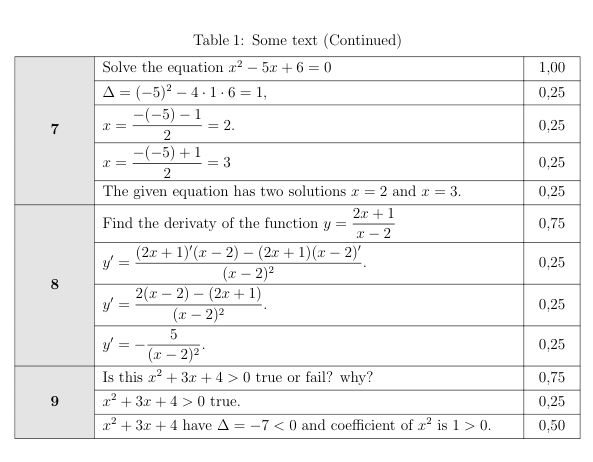
My questions:
 At the page 2, how to reset header `Problem & Content & Point \\` like the first page;