samcarter

> This is part of the Summer of Code 2022 series, see https://topanswers.xyz/tex?q=2059 for more information
Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
```
Triangle T(n)=n(n+1)/2 1, 3, 6, 10, 15, ...
Pentagonal P(n)=n(3n−1)/2 1, 5, 12, 22, 35, ...
Hexagonal H(n)=n(2n−1) 1, 6, 15, 28, 45, ...
```
It can be verified that T(285) = P(165) = H(143) = 40755.
Find the next triangle number that is also pentagonal and hexagonal.
(this programming puzzle is taken from https://projecteuler.net/problem=45, licensed under CC BY-NC-SA 4.0)

Top Answer
frougon

\* This line is not a spoiler. \*
Here are two ways using `xint`, which performs computations with arbitrarily long integers (among others!). This is however *much slower* than my [first implementation](https://topanswers.xyz/tex?q=2087#a2334) which uses TeX `\count` registers via expl3 int variables.
# First way: with `xint` user variables
This is the slowest way: reaching `T(55385) = P(31977) = H(27693) = 1533776805` takes about 79 seconds on my computer. All integers are stored in `xint` user variables.
```
\documentclass{article}
\usepackage{xintexpr}
\xintdefiifunc T(n) := n*(n+1)/2;
\xintdefiifunc P(n) := n*(3*n-1)/2;
\xintdefiifunc H(n) := n*(2*n-1);
\ExplSyntaxOn
\bool_new:N \l__socix_stop_flag_bool
\cs_new_protected:Npn \socix_find_coincidences:
{
\bool_set_false:N \l__socix_stop_flag_bool
\xintdefiivar n, i, j := 0, 0, 0;
\bool_do_until:Nn \l__socix_stop_flag_bool
{
% \iow_term:x { n~ =~ \xintiieval{n} }
\xintdefiivar nb_matches := 0;
\xintdefiivar valT := T(n);
% Advance i to the smallest value ≥ its current value such that
% P(i) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\xintdefiivar valP := P(i);
\xintiiifLt { \xintiieval{valP} } { \xintiieval{valT} }
{ \xintdefiivar i := i + 1; }
{ \prg_break: }
}
\prg_break_point:
% If P(i) = T(n), increase nb_matches
\xintiiifEq { \xintiieval{valP} } { \xintiieval{valT} }
{ \xintdefiivar nb_matches := nb_matches + 1; }
{ }
% Advance j to the smallest value ≥ its current value such that
% H(j) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\xintdefiivar valH := H(j);
\xintiiifLt { \xintiieval{valH} } { \xintiieval{valT} }
{ \xintdefiivar j := j + 1; }
{ \prg_break: }
}
\prg_break_point:
% If H(j) = T(n), increase nb_matches
\xintiiifEq { \xintiieval{valH} } { \xintiieval{valT} }
{ \xintdefiivar nb_matches := nb_matches + 1; }
{ }
\xintiiifEq { \xintiieval{nb_matches} } { 2 }
{
\par \noindent
\c_math_toggle_token
T(\xintiieval{n}) = P(\xintiieval{i})
= H(\xintiieval{j}) = \xintiieval{valT}
\c_math_toggle_token
% We need to stop somewhere. :-P
\xintiiifLt { \xintiieval{valT} } { 1533776805 }% 57722156241751
{ }
{ \bool_set_true:N \l__socix_stop_flag_bool }
}
{ }
\xintdefiivar n := n + 1;
}
}
\cs_new_eq:NN \socIXFindCoincidences \socix_find_coincidences:
\ExplSyntaxOff
\begin{document}
\socIXFindCoincidences
\end{document}
```
# Second way: integers stored in expl3 tl vars
This is a bit faster: reaching `T(55385) = P(31977) = H(27693) = 1533776805` takes about 50 seconds on my computer. All integers are stored in expl3 tl vars, i.e. parameterless macros.
```
\documentclass{article}
\usepackage{xintexpr}
\xintdefiifunc T(n) := n*(n+1)/2;
\xintdefiifunc P(n) := n*(3*n-1)/2;
\xintdefiifunc H(n) := n*(2*n-1);
\ExplSyntaxOn
\tl_new:N \l__socix_nb_matches_tl
\tl_new:N \l__socix_n_tl
\tl_new:N \l__socix_i_tl
\tl_new:N \l__socix_j_tl
\tl_new:N \l__socix_valT_tl
\tl_new:N \l__socix_valP_tl
\tl_new:N \l__socix_valH_tl
\bool_new:N \l__socix_stop_flag_bool
\cs_new_protected:Npn \__socix_int_incr:N #1
{
\tl_set:Nx #1 { \xintiieval { #1 + 1 } }
}
\cs_new_protected:Npn \socix_find_coincidences:
{
\bool_set_false:N \l__socix_stop_flag_bool
\clist_map_inline:nn { \l__socix_n_tl, \l__socix_i_tl, \l__socix_j_tl }
{ \tl_set:Nn ##1 { 0 } }
\bool_do_until:Nn \l__socix_stop_flag_bool
{
% \iow_term:x { n~ =~ \l__socix_n_tl }
\tl_set:Nn \l__socix_nb_matches_tl { 0 }
\tl_set:Nx \l__socix_valT_tl { \xintiieval { T(\l__socix_n_tl) } }
% Advance i to the smallest value ≥ its current value such that
% P(i) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\tl_set:Nx \l__socix_valP_tl { \xintiieval { P(\l__socix_i_tl) } }
\xintiiifLt { \l__socix_valP_tl } { \l__socix_valT_tl }
{ \__socix_int_incr:N \l__socix_i_tl }
{ \prg_break: }
}
\prg_break_point:
% If P(i) = T(n), increase nb_matches
\xintiiifEq { \l__socix_valP_tl } { \l__socix_valT_tl }
{ \__socix_int_incr:N \l__socix_nb_matches_tl }
{ }
% Advance j to the smallest value ≥ its current value such that
% H(j) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\tl_set:Nx \l__socix_valH_tl { \xintiieval { H(\l__socix_j_tl) } }
\xintiiifLt { \l__socix_valH_tl } { \l__socix_valT_tl }
{ \__socix_int_incr:N \l__socix_j_tl }
{ \prg_break: }
}
\prg_break_point:
% If H(j) = T(n), increase \l__socix_nb_matches_int
\xintiiifEq { \l__socix_valH_tl } { \l__socix_valT_tl }
{ \__socix_int_incr:N \l__socix_nb_matches_tl }
{ }
\xintiiifEq { \l__socix_nb_matches_tl } { 2 }
{
\par \noindent
\c_math_toggle_token
T(\l__socix_n_tl) = P(\l__socix_i_tl)
= H(\l__socix_j_tl) = \l__socix_valT_tl
\c_math_toggle_token
% We need to stop somewhere. :-P
\xintiiifLt { \l__socix_valT_tl } { 1533776805 }% 57722156241751
{ }
{ \bool_set_true:N \l__socix_stop_flag_bool }
}
{ }
\__socix_int_incr:N \l__socix_n_tl
}
}
\cs_new_eq:NN \socIXFindCoincidences \socix_find_coincidences:
\ExplSyntaxOff
\begin{document}
\socIXFindCoincidences
\end{document}
```
# Output
Both examples produce the following output:
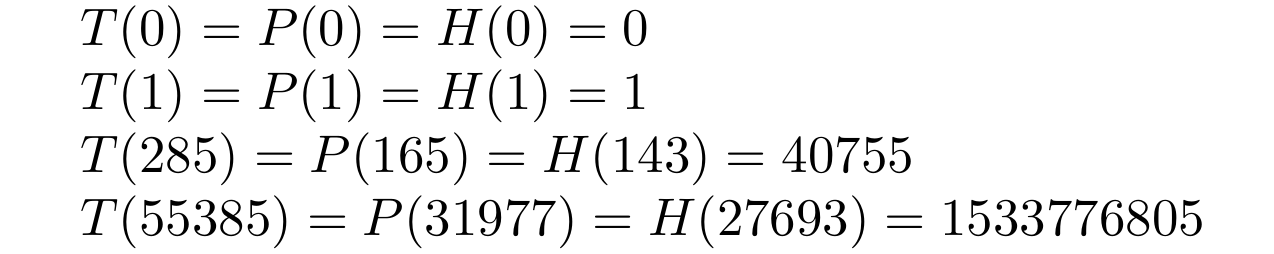
# What's next?
As shown by the following Python code, the next line to display is:
T(10744501) = P(6203341) = H(5372251) = 57722156241751
```
#! /usr/bin/env python3
import sys
from math import sqrt
def T(n):
return int(n*(n+1)/2)
def P(n):
return int(n*(3*n-1)/2)
def H(n):
return int(n*(2*n-1))
def main():
n = i = j = 0
while True:
matches = 0
valT = T(n)
while True:
valP = P(i)
if valP >= valT: break
i += 1
if valP == valT:
matches += 1
while True:
valH = H(j)
if valH >= valT: break
j += 1
if valH == valT:
matches += 1
if matches == 2:
print(f"T({n}) = P({i}) = H({j}) = {valT}")
n += 1
sys.exit(0)
if __name__ == "__main__": main()
```
The result `T(10744501) = P(6203341) = H(5372251) = 57722156241751` is clearly out of reach for standard arithmetic using TeX `\count` registers, however the `xint`-based codes posted here should be able to get there given enough time—I expect something on the order of two or three hours with the second code of this answer.
Answer #2
frougon

\* This line is not a spoiler. \*
The following code uses TeX integer arithmetic; it is fast (1.4 second on my computer), but the arithmetic overflow is quite close. It would probably be wise to use another language for this... or, if one *really* wants to do this with TeX, use some package like [xint](https://ctan.org/pkg/xint) that can compute with arbitrarily large integers (see my [other answer](https://topanswers.xyz/tex?q=2087#a2335)).
The algorithm used here exploits the fact that the three sequences are strictly increasing (my other answer has the algorithm implemented in Python, probably easier to read this way—before starting to work with `\count` registers, I wanted to be sure that the goal was reachable without triggering the dreaded arithmetic overflow! :)).
```
\documentclass{article}
\ExplSyntaxOn
\int_new:N \l__socix_nb_matches_int
\int_new:N \l__socix_n_int
\int_new:N \l__socix_i_int
\int_new:N \l__socix_j_int
\int_new:N \l__socix_valT_int
\int_new:N \l__socix_valP_int
\int_new:N \l__socix_valH_int
\bool_new:N \l__socix_stop_flag_bool
\cs_new_protected:Npn \socix_find_coincidences:
{
\int_zero:N \l__socix_n_int
\int_zero:N \l__socix_i_int
\int_zero:N \l__socix_j_int
\bool_set_false:N \l__socix_stop_flag_bool
\bool_do_until:Nn \l__socix_stop_flag_bool
{
\int_zero:N \l__socix_nb_matches_int
\int_set:Nn \l__socix_valT_int
{ \l__socix_n_int*(\l__socix_n_int + 1)/2 }
% Advance i to the smallest value ≥ its current value such that
% P(i) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\int_set:Nn \l__socix_valP_int
{ \l__socix_i_int*(3*\l__socix_i_int - 1)/2 }
\int_compare:nNnF { \l__socix_valP_int } < { \l__socix_valT_int }
{ \prg_break: }
\int_incr:N \l__socix_i_int
}
\prg_break_point:
% If P(i) = T(n), increase \l__socix_nb_matches_int
\int_compare:nNnT { \l__socix_valP_int } = { \l__socix_valT_int }
{
\int_incr:N \l__socix_nb_matches_int
}
% Advance j to the smallest value ≥ its current value such that
% H(j) >= T(n).
\bool_do_while:Nn \c_true_bool
{
\int_set:Nn \l__socix_valH_int
{ \l__socix_j_int*(2*\l__socix_j_int - 1) }
\int_compare:nNnF { \l__socix_valH_int } < { \l__socix_valT_int }
{ \prg_break: }
\int_incr:N \l__socix_j_int
}
\prg_break_point:
% If H(j) = T(n), increase \l__socix_nb_matches_int
\int_compare:nNnT { \l__socix_valH_int } = { \l__socix_valT_int }
{
\int_incr:N \l__socix_nb_matches_int
}
\int_compare:nNnT { \l__socix_nb_matches_int } = { 2 }
{
\par \noindent
\c_math_toggle_token
T(\int_use:N \l__socix_n_int) = P(\int_use:N \l__socix_i_int)
= H(\int_use:N \l__socix_j_int) = \int_use:N \l__socix_valT_int
\c_math_toggle_token
% We need to stop somewhere... and preferably before an arithmetic
% overflow. :-P
\int_compare:nNnT { \l__socix_valT_int } > { 1500000000 }
{ \bool_set_true:N \l__socix_stop_flag_bool }
}
\int_incr:N \l__socix_n_int
}
}
\cs_new_eq:NN \socIXFindCoincidences \socix_find_coincidences:
\ExplSyntaxOff
\begin{document}
\socIXFindCoincidences
\end{document}
```