samcarter

> This is part of the Summer of Code 2022 series, see https://topanswers.xyz/tex?q=2059 for more information
The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime.
There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97.
How many circular primes are there below one million?
(this programming puzzle is taken from https://projecteuler.net/problem=35, licensed under CC BY-NC-SA 4.0)

Top Answer
Skillmon

Duck wants to solve again:
Of course the functions here are expandable :) They take a parameter being the upper bound for the circular primes.
The following implements a fastish check for primes (can be faster, but fine enough), and a fast integer square root (which actually saves us around 2 seconds with the upper bound being 1000000, for less just checking whether the current square is bigger than the number is faster).
```
\documentclass{article}
\usepackage{ducksay}
\makeatletter
% integer square root implementation
% based on http://www.azillionmonkeys.com/qed/sqroot.html section 3c
% build look up table
\def\cp@tmp
{%
\advance\count2by1
\expandafter\def\csname cp@sqrt@\the\count2 \endcsname
}
\count2=-1
\cp@tmp{0} \cp@tmp{16} \cp@tmp{22} \cp@tmp{27}
\cp@tmp{32} \cp@tmp{35} \cp@tmp{39} \cp@tmp{42}
\cp@tmp{45} \cp@tmp{48} \cp@tmp{50} \cp@tmp{53}
\cp@tmp{55} \cp@tmp{57} \cp@tmp{59} \cp@tmp{61}
\cp@tmp{64} \cp@tmp{65} \cp@tmp{67} \cp@tmp{69}
\cp@tmp{71} \cp@tmp{73} \cp@tmp{75} \cp@tmp{76}
\cp@tmp{78} \cp@tmp{80} \cp@tmp{81} \cp@tmp{83}
\cp@tmp{84} \cp@tmp{86} \cp@tmp{87} \cp@tmp{89}
\cp@tmp{90} \cp@tmp{91} \cp@tmp{93} \cp@tmp{94}
\cp@tmp{96} \cp@tmp{97} \cp@tmp{98} \cp@tmp{99}
\cp@tmp{101} \cp@tmp{102} \cp@tmp{103} \cp@tmp{104}
\cp@tmp{106} \cp@tmp{107} \cp@tmp{108} \cp@tmp{109}
\cp@tmp{110} \cp@tmp{112} \cp@tmp{113} \cp@tmp{114}
\cp@tmp{115} \cp@tmp{116} \cp@tmp{117} \cp@tmp{118}
\cp@tmp{119} \cp@tmp{120} \cp@tmp{121} \cp@tmp{122}
\cp@tmp{123} \cp@tmp{124} \cp@tmp{125} \cp@tmp{126}
\cp@tmp{128} \cp@tmp{128} \cp@tmp{129} \cp@tmp{130}
\cp@tmp{131} \cp@tmp{132} \cp@tmp{133} \cp@tmp{134}
\cp@tmp{135} \cp@tmp{136} \cp@tmp{137} \cp@tmp{138}
\cp@tmp{139} \cp@tmp{140} \cp@tmp{141} \cp@tmp{142}
\cp@tmp{143} \cp@tmp{144} \cp@tmp{144} \cp@tmp{145}
\cp@tmp{146} \cp@tmp{147} \cp@tmp{148} \cp@tmp{149}
\cp@tmp{150} \cp@tmp{150} \cp@tmp{151} \cp@tmp{152}
\cp@tmp{153} \cp@tmp{154} \cp@tmp{155} \cp@tmp{155}
\cp@tmp{156} \cp@tmp{157} \cp@tmp{158} \cp@tmp{159}
\cp@tmp{160} \cp@tmp{160} \cp@tmp{161} \cp@tmp{162}
\cp@tmp{163} \cp@tmp{163} \cp@tmp{164} \cp@tmp{165}
\cp@tmp{166} \cp@tmp{167} \cp@tmp{167} \cp@tmp{168}
\cp@tmp{169} \cp@tmp{170} \cp@tmp{170} \cp@tmp{171}
\cp@tmp{172} \cp@tmp{173} \cp@tmp{173} \cp@tmp{174}
\cp@tmp{175} \cp@tmp{176} \cp@tmp{176} \cp@tmp{177}
\cp@tmp{178} \cp@tmp{178} \cp@tmp{179} \cp@tmp{180}
\cp@tmp{181} \cp@tmp{181} \cp@tmp{182} \cp@tmp{183}
\cp@tmp{183} \cp@tmp{184} \cp@tmp{185} \cp@tmp{185}
\cp@tmp{186} \cp@tmp{187} \cp@tmp{187} \cp@tmp{188}
\cp@tmp{189} \cp@tmp{189} \cp@tmp{190} \cp@tmp{191}
\cp@tmp{192} \cp@tmp{192} \cp@tmp{193} \cp@tmp{193}
\cp@tmp{194} \cp@tmp{195} \cp@tmp{195} \cp@tmp{196}
\cp@tmp{197} \cp@tmp{197} \cp@tmp{198} \cp@tmp{199}
\cp@tmp{199} \cp@tmp{200} \cp@tmp{201} \cp@tmp{201}
\cp@tmp{202} \cp@tmp{203} \cp@tmp{203} \cp@tmp{204}
\cp@tmp{204} \cp@tmp{205} \cp@tmp{206} \cp@tmp{206}
\cp@tmp{207} \cp@tmp{208} \cp@tmp{208} \cp@tmp{209}
\cp@tmp{209} \cp@tmp{210} \cp@tmp{211} \cp@tmp{211}
\cp@tmp{212} \cp@tmp{212} \cp@tmp{213} \cp@tmp{214}
\cp@tmp{214} \cp@tmp{215} \cp@tmp{215} \cp@tmp{216}
\cp@tmp{217} \cp@tmp{217} \cp@tmp{218} \cp@tmp{218}
\cp@tmp{219} \cp@tmp{219} \cp@tmp{220} \cp@tmp{221}
\cp@tmp{221} \cp@tmp{222} \cp@tmp{222} \cp@tmp{223}
\cp@tmp{224} \cp@tmp{224} \cp@tmp{225} \cp@tmp{225}
\cp@tmp{226} \cp@tmp{226} \cp@tmp{227} \cp@tmp{227}
\cp@tmp{228} \cp@tmp{229} \cp@tmp{229} \cp@tmp{230}
\cp@tmp{230} \cp@tmp{231} \cp@tmp{231} \cp@tmp{232}
\cp@tmp{232} \cp@tmp{233} \cp@tmp{234} \cp@tmp{234}
\cp@tmp{235} \cp@tmp{235} \cp@tmp{236} \cp@tmp{236}
\cp@tmp{237} \cp@tmp{237} \cp@tmp{238} \cp@tmp{238}
\cp@tmp{239} \cp@tmp{240} \cp@tmp{240} \cp@tmp{241}
\cp@tmp{241} \cp@tmp{242} \cp@tmp{242} \cp@tmp{243}
\cp@tmp{243} \cp@tmp{244} \cp@tmp{244} \cp@tmp{245}
\cp@tmp{245} \cp@tmp{246} \cp@tmp{246} \cp@tmp{247}
\cp@tmp{247} \cp@tmp{248} \cp@tmp{248} \cp@tmp{249}
\cp@tmp{249} \cp@tmp{250} \cp@tmp{250} \cp@tmp{251}
\cp@tmp{251} \cp@tmp{252} \cp@tmp{252} \cp@tmp{253}
\cp@tmp{253} \cp@tmp{254} \cp@tmp{254} \cp@tmp{255}
\let\cp@tmp\cp@undefined
\def\cp@sqrt#1%
{%
\ifnum#1<"10000
\ifnum#1<"100
(\csname cp@sqrt@#1\endcsname-8)/16
\else
\ifnum#1<"1000
\ifnum#1<"400
\expandafter\cp@sqrt@c
\the\numexpr
(\csname cp@sqrt@\the\numexpr(#1-2)/4\relax\endcsname-4)/8+1%
\relax;{#1}%
\else
\expandafter\cp@sqrt@c
\the\numexpr
(\csname cp@sqrt@\the\numexpr(#1-8)/16\relax\endcsname-2)/4+1%
\relax;{#1}%
\fi
\else
\ifnum#1<"4000
\expandafter\cp@sqrt@c
\the\numexpr
(\csname cp@sqrt@\the\numexpr(#1-32)/64\relax\endcsname-1)/2+1%
\relax;{#1}%
\else
\expandafter\cp@sqrt@c
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-128)/256\relax\endcsname+1%
\relax;{#1}%
\fi
\fi
\fi
\else
\ifnum#1<"1000000
\ifnum#1<"100000
\ifnum#1<"40000
\expandafter\cp@sqrt@b
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-512)/1024\relax\endcsname
*2%
\relax;{#1}%
\else
\expandafter\cp@sqrt@b
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-2048)/4096\relax\endcsname
*4%
\relax;{#1}%
\fi
\else
\ifnum#1<"400000
\expandafter\cp@sqrt@b
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-8192)/16384\relax\endcsname
*8%
\relax;{#1}%
\else
\expandafter\cp@sqrt@b
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-32768)/65536\relax\endcsname
*16%
\relax;{#1}%
\fi
\fi
\else
\ifnum#1<"10000000
\ifnum#1<"4000000
\expandafter\cp@sqrt@a
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-131072)/262144\relax\endcsname
*32%
\relax;{#1}%
\else
\expandafter\cp@sqrt@a
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-524288)/1048576\relax\endcsname
*64%
\relax;{#1}%
\fi
\else
\ifnum#1<"40000000
\expandafter\cp@sqrt@a
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-2097152)/4194304\relax\endcsname
*128%
\relax;{#1}%
\else
\expandafter\cp@sqrt@a
\the\numexpr
\csname cp@sqrt@\the\numexpr(#1-8388608)/16777216\relax\endcsname
*256%
\relax;{#1}%
\fi
\fi
\fi
\fi
}
\def\cp@sqrt@a#1;#2%
{\expandafter\cp@sqrt@b\the\numexpr(#1+(#2-(#1-1)/2)/#1)/2\relax;{#2}}%
\def\cp@sqrt@b#1;#2%
{\expandafter\cp@sqrt@c\the\numexpr(#1+(#2-(#1-1)/2)/#1)/2\relax;{#2}}%
\def\cp@sqrt@c#1;#2{#1\ifnum\numexpr#1*#1\relax>#2 -1\fi}
% quickish check for a prime
\def\cp@ifisprime#1%
{%
\cp@ifisprime@onefour@twothreefive
;#1;4;2;3;5;%
\cp@ifisprime@false
;1;#1;2;3;5;%
\cp@ifisprime@false
;1;4;#1;3;5;%
\cp@ifisprime@true@fast
;1;4;2;#1;5;%
\cp@ifisprime@true@fast
;1;4;2;3;#1;%
\cp@ifisprime@true@fast
;1;4;2;3;5;%
\cp@divisable@two
#1;2;4;6;8;\cp@ifisprime@false
0;#1;4;6;8;\cp@ifisprime@false
0;2;#1;6;8;\cp@ifisprime@false
0;2;4;#1;8;\cp@ifisprime@false
0;2;4;6;#1;\cp@ifisprime@false
0;2;4;6;8;%
\cp@divisable@five
#1;\cp@ifisprime@false
5;%
\cp@ifdivisable{#1}3%
\expandafter\cp@ifisprime@loop\the\numexpr\cp@sqrt{#1}\relax;{#1}%
\cp@ifisprime@true
}
\expanded{\unexpanded{\def\cp@ifisprime@colon#1;}\expandafter}\expandafter
{\cp@ifisprime{#1}}
\def\cp@ifisprime@true#1#2{#1}
\def\cp@ifisprime@false
#1\cp@ifisprime@true#2#3%
{#3}%
\def\cp@ifisprime@true@fast
#1\cp@ifisprime@true#2#3%
{#2}%
\def\cp@ifisprime@onefour@twothreefive#1;1;4;2;3;5;{}
\def\cp@divisable@two#10;#22;#34;#46;#58;{}
\def\cp@divisable@five#15;{}
\def\cp@ifdivisable#1#2%
{%
\if0\the\numexpr#1-(#1/#2)*#2\relax
\cp@divisable
\fi
}
\def\cp@divisable\fi#1\cp@ifisprime@true#2#3{\fi#3}
\def\cp@ifisprime@loop{\cp@ifisprime@loop@5;}
\def\cp@ifisprime@loop@#1;#2;#3%
{%
\ifnum#1>#2 \cp@ifisprime@loop@done\fi
\cp@ifdivisable{#3}{#1}%
\expandafter\cp@ifisprime@loop@aux\the\numexpr#1+2\relax;{#3}%
\expandafter\cp@ifisprime@loop@\the\numexpr#1+6\relax;#2;{#3}%
}
\expanded{\unexpanded{\def\cp@ifisprime@loop@aux#1;#2}\expandafter}\expandafter{\cp@ifdivisable{#2}{#1}}
\def\cp@ifisprime@loop@done\fi#1\cp@ifisprime@true#2#3{\fi#2}
% circular checking is quite easy, just rotate until number equals original
% number again, check prime each rotation
\def\cp@check@circulars#1{\cp@circle#1;{#1}}
\def\cp@circle#1#2;#3%
{%
\ifnum#2#1=#3 \cp@circle@done\fi
\expandafter\cp@ifisprime@colon\number#2#1;{\cp@circle#2#1;{#3}}{}%
}
\def\cp@circle@done\fi\expandafter\cp@ifisprime@colon\number#1;#2#3{\fi+1}
% first step just ensure only digits (no count etc.) is input
\def\circprime#1%
{%
\the\numexpr
\expandafter\cp@\the\numexpr#1\relax;%
\relax
}
% handle special case 2 and init loop
\def\cp@#1;{\ifnum2<#1 1\fi\cp@loop3;{#1}}
% looping is quite simple. We only check every odd integer in the first place.
\def\cp@loop#1;#2%
{%
\ifnum#1>#2 \cp@loop@done\fi
\cp@ifisprime{#1}%
{\cp@check@circulars{#1}}
{}%
\expandafter\cp@loop\the\numexpr#1+2\relax;{#2}%
}
\def\cp@loop@done\fi#1;#2{\fi}
\makeatother
\newcommand\solveSoC{\ducksay[vpad=1]{\circprime{1000000}}}
\begin{document}
\solveSoC
\end{document}
```
As promised a version that is a bit more optimised. This sorts out everything that can't be a circular prime because one permutation will be dividable by either 2 or 5 in just two steps of expansion. It is also faster without the square root (above might also be faster, but I like to keep the square root code).
The result of this finds the circular primes smaller than 1000000 in less than 4 seconds on my laptop, so no further optimization required.
```
\documentclass{article}
\usepackage{ducksay}
\makeatletter
% quickish check for a circular prime (everything containing a digit dividable
% by 2 or 5 can't be a circular prime)
\def\cp@ifiscircprime#1%
{%
\cp@divisable@twofive
#1;\cp@ifiscircprime@false0;{}%
#1;\cp@ifiscircprime@false2;{}%
#1;\cp@ifiscircprime@false4;{}%
#1;\cp@ifiscircprime@false6;{}%
#1;\cp@ifiscircprime@false8;{}%
#1;\cp@ifiscircprime@false5;{}%
\cp@ifdivisable{#1}3%
\cp@ifiscircprime@loop5;{#1}\cp@ifiscircprime@loop@end
\cp@ifiscircprime@circle#1;{#1}\cp@ifiscircprime@circle@end
\cp@ifiscircprime@true
}
\def\cp@ifiscircprime@circle#1#2;#3%
{%
\ifnum#2#1=#3 \cp@ifiscircprime@circle@done\fi
\expandafter\cp@ifiscircprime@circle@aux\number#2#1;%
\cp@ifiscircprime@circle#2#1;{#3}%
}
\def\cp@ifiscircprime@circle@aux#1;%
{\cp@ifiscircprime@loop5;{#1}\cp@ifiscircprime@loop@end}
\def\cp@ifiscircprime@circle@done\fi#1\cp@ifiscircprime@circle@end{\fi}
\expanded{\unexpanded{\def\cp@ifiscircprime@colon#1;}\expandafter}\expandafter
{\cp@ifiscircprime{#1}}
\def\cp@ifiscircprime@true{+1}
\def\cp@ifiscircprime@false#1\cp@ifiscircprime@true{}%
\def\cp@ifiscircprime@true@fast#1\cp@ifiscircprime@true{+1}%
\def\cp@ifiscircprime@onefour@twothreefive#1;1;4;2;3;5;{}
\def\cp@divisable@twofive #10#2;#3#42#5;#6#74#8;#9{#3#6#9\cp@divisable@twofive@}
\def\cp@divisable@twofive@#16#2;#3#48#5;#6#75#8;#9{#3#6#9}
\def\cp@divisable@five#15#2;{}
\def\cp@ifdivisable#1#2%
{%
\if0\the\numexpr#1-(#1/#2)*#2\relax
\cp@divisable
\fi
}
\def\cp@divisable\fi#1\cp@ifiscircprime@true{\fi}
\def\cp@ifiscircprime@loop#1;#2%
{%
\ifnum\numexpr#1*#1\relax>#2 \cp@ifiscircprime@loop@done\fi
\cp@ifdivisable{#2}{#1}%
\expandafter\cp@ifiscircprime@loop@aux\the\numexpr#1+2\relax;{#2}%
\expandafter\cp@ifiscircprime@loop\the\numexpr#1+6\relax;{#2}%
}
\expanded{\unexpanded{\def\cp@ifiscircprime@loop@aux#1;#2}\expandafter}\expandafter{\cp@ifdivisable{#2}{#1}}
\def\cp@ifiscircprime@loop@done\fi#1\cp@ifiscircprime@loop@end{\fi}
% first step just ensure only digits (no count etc.) is input
\def\circprime#1%
{%
\the\numexpr
\expandafter\cp@\the\numexpr#1\relax;%
\relax
}
% handle special case 2 and init loop
\def\cp@#1;%
{%
\ifnum2<#1 +1\fi
\ifnum3<#1 +1\fi
\ifnum5<#1 +1\fi
\ifnum7<#1 +1\fi
\cp@loop11;{#1}%
}
% looping is quite simple. We only check every odd integer in the first place.
\def\cp@loop#1;#2%
{%
\ifnum#1>#2 \cp@loop@done\fi
\cp@ifiscircprime{#1}%
\expandafter\cp@loop\the\numexpr#1+2\relax;{#2}%
}
\def\cp@loop@done\fi#1;#2{\fi}
\makeatother
\newcommand\solveSoC{\ducksay[vpad=1]{\circprime{1000000}}}
\begin{document}
\solveSoC
\end{document}
```
Output of both code blocks:
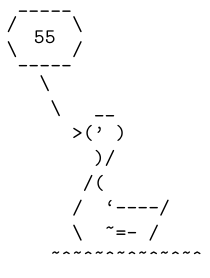
Answer #2
frougon

I compiled the following code using `pdflatex` after rebuilding the format with increased memory parameters (see below). Compiling the .tex file requires about 2 minutes on my old computer.
There is nothing very fancy here: I use [this algorithm](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes#Pseudocode) (Sieve of Eratosthenes) in order to find all prime numbers not greater than the specified number, then test each of these to determine whether it is circular. Rotation of the digits is done using integer arithmetic.
```
\documentclass{article}
\ExplSyntaxOn
\int_new:N \l__socvi_ies_a_int
\int_new:N \l__socvi_ies_a_squared_int
\cs_new_protected:Npn \socvi_init_eratosthenes_sieve:n #1
{
\int_set:Nn \l__socvi_ies_a_int { 2 }
\int_set:Nn \l__socvi_ies_a_squared_int { 4 }
\int_until_do:nNnn { \l__socvi_ies_a_squared_int } > {#1}
{
\iow_term:x
{ Starting~ sieve~ loop~ with~ a²~ =~ \int_use:N
\l__socvi_ies_a_squared_int }
\socvi_if_is_prime:VT \l__socvi_ies_a_int
{
\int_set_eq:NN \l_tmpa_int \l__socvi_ies_a_squared_int
\int_until_do:nNnn { \l_tmpa_int } > {#1}
{
% Mark \l_tmpa_int as non-prime
\tl_clear_new:c { l__socvi_sieve_ \int_use:N \l_tmpa_int _tl }
\int_add:Nn \l_tmpa_int { \l__socvi_ies_a_int }
}
}
\int_incr:N \l__socvi_ies_a_int
\int_set:Nn \l__socvi_ies_a_squared_int
{ \l__socvi_ies_a_int * \l__socvi_ies_a_int }
}
}
\prg_new_conditional:Npnn \socvi_if_is_prime:n #1 { p, T, F, TF }
{
\tl_if_exist:cTF { l__socvi_sieve_#1_tl }
{ \prg_return_false: }
{ \prg_return_true: }
}
\prg_generate_conditional_variant:Nnn \socvi_if_is_prime:n { V } { T, F }
\cs_new_protected:Npn \socvi_set_to_primes_at_most:Nn #1#2
{
\iow_term:x { Building~ the~ list~ of~ primes~ not~ greater~ than~ #2... }
\seq_clear:N #1
% Let's add 2 manually so that we can then iterate on odd integers only.
\seq_put_right:Nn #1 { 2 }
\int_step_inline:nnnn { 3 } { 2 } {#2}
{
% \iow_term:x { Testing~ primality~ of~ ##1 }
\socvi_if_is_prime:nT {##1} { \seq_put_right:Nn #1 {##1} }
}
}
\seq_new:N \l__socvi_ppam_seq
\cs_new_protected:Npn \socvi_print_primes_at_most:n #1
{
\socvi_set_to_primes_at_most:Nn \l__socvi_ppam_seq {#1}
\seq_use:Nn \l__socvi_ppam_seq { ,~ }
}
% Rotate \l__socvi_pic_current_int right by one place
\cs_new_protected:Npn \__socvi_pic_rotate_right:
{
\int_set:Nn \l__socvi_pic_current_int
{
\int_mod:nn { \l__socvi_pic_current_int } { 10 }
* 1 \prg_replicate:nn { \l__socvi_pic_leftmost_digit_rank_int } { 0 }
+
\int_div_truncate:nn { \l__socvi_pic_current_int } { 10 }
}
}
\int_new:N \l__socvi_pic_leftmost_digit_rank_int
\int_new:N \l__socvi_pic_nb_rotations_left_int
\int_new:N \l__socvi_pic_current_int
\bool_new:N \l__socvi_pic_result_true_bool
\prg_new_protected_conditional:Npnn \socvi_prime_if_circular:n #1 { T, F, TF }
{
\int_set:Nn \l__socvi_pic_leftmost_digit_rank_int { \tl_count:n {#1} - 1 }
\int_set_eq:NN \l__socvi_pic_nb_rotations_left_int
\l__socvi_pic_leftmost_digit_rank_int
\int_set:Nn \l__socvi_pic_current_int {#1}
\bool_set_true:N \l__socvi_pic_result_true_bool
\bool_while_do:nn
{
\bool_lazy_and_p:nn
{ \int_compare_p:nNn { \l__socvi_pic_nb_rotations_left_int } > { 0 } }
{ \l__socvi_pic_result_true_bool }
}
{
\int_decr:N \l__socvi_pic_nb_rotations_left_int
\__socvi_pic_rotate_right:
\socvi_if_is_prime:VF \l__socvi_pic_current_int
{ \bool_set_false:N \l__socvi_pic_result_true_bool }
}
\bool_if:NTF \l__socvi_pic_result_true_bool
{ \prg_return_true: }
{ \prg_return_false: }
}
\seq_new:N \l__socvi_stcpam_primes_seq
\cs_new_protected:Npn \socvi_set_to_circular_primes_at_most:Nn #1#2
{
\iow_term:x
{ Building~ the~ list~ of~ circular~ primes~ not~ greater~ than~ #2... }
\seq_clear:N #1
% Let's add 2 manually so that we can then iterate on odd integers only.
\seq_put_right:Nn #1 { 2 }
\int_step_inline:nnnn { 3 } { 2 } {#2}
{
\socvi_if_is_prime:nT {##1}
{
% \iow_term:x { Testing~ circularity~ of~ ##1 }
\socvi_prime_if_circular:nT {##1} { \seq_put_right:Nn #1 {##1} }
}
}
}
\seq_new:N \l__socvi_pcpam_seq
\cs_new:Npn \__socvi_pcpam_sentence:nnn #1#2#3 { }
\cs_generate_variant:Nn \__socvi_pcpam_sentence:nnn { xnx }
\cs_new_protected:Npn \socvi_print_circular_primes_at_most:nn #1#2
{
\cs_set:Npn \__socvi_pcpam_sentence:nnn ##1##2##3 {#2}
\socvi_set_to_circular_primes_at_most:Nn \l__socvi_pcpam_seq {#1}
\__socvi_pcpam_sentence:xnx { \seq_count:N \l__socvi_pcpam_seq } {#1}
{ \seq_use:Nnnn \l__socvi_pcpam_seq { ~and~ } { ,~ } { ,~and~ } }
}
\cs_new_eq:NN \initEratosthenesSieve \socvi_init_eratosthenes_sieve:n
\cs_new_eq:NN \setToPrimesAtMost \socvi_set_to_primes_at_most:Nn
\cs_new_eq:NN \printPrimesAtMost \socvi_print_primes_at_most:n
\cs_new_eq:NN \printCircularPrimesAtMost \socvi_print_circular_primes_at_most:nn
\ExplSyntaxOff
\begin{document}
\initEratosthenesSieve{1000000}
\noindent
All prime numbers less than or equal to 200: \printPrimesAtMost{200}.
\bigskip\noindent
\printCircularPrimesAtMost{1000000}{%
There are #1~circular prime numbers less than or equal to~#2. These numbers
are #3.}
\end{document}
```

# Memory parameters
I built my `pdflatex` format with this in /etc/texmf/texmf.d/00local-increase-memory-size.cnf:
```
main_memory = 8000000 % words of inimemory available; also applies to inimf&mp
extra_mem_top = 70000000 % extra high memory for chars, tokens, etc.
extra_mem_bot = 70000000 % extra low memory for boxes, glue, breakpoints, etc.
pool_size = 30500000
max_strings = 1000000
hash_extra = 1200000
```
Actually, only the last three lines were added today; I've had the other ones for several years, maybe they aren't needed to compile this document. After editing the file, I rebuilt the `pdflatex` format using the following command, run as root:
```
update-texmf && fmtutil-sys --byfmt pdflatex
```
This is with the TeX Live distribution as shipped by Debian; details may vary depending on your operating system and TeX distribution.