samcarter

> This is part of the Summer of Code 2022 series, see https://topanswers.xyz/tex?q=2059 for more information
A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
Find the largest palindrome made from the product of two 3-digit numbers.
(this programming puzzle is taken from https://projecteuler.net/problem=4, licensed under CC BY-NC-SA 4.0)

Top Answer
frougon

\* This line is not a spoiler. \*
The following code does the job with two little optimizations:
- the `\sociv_is_palindrome:nTF` conditional stops as soon as two different digits have been found in “complementary positions” (like first and last, second and penultimate, etc.);
- we skip all cases where one of the factors is a multiple of ten (by hypothesis, all numbers considered in the exercise are written without any leading zero, therefore no number greater than zero can be a palindrome and a multiple of ten).
```
\documentclass{article}
\ExplSyntaxOn
\int_new:N \l__sociv_ispal_current_index_int
\int_new:N \l__sociv_ispal_last_index_int
\bool_new:N \l__sociv_ispal_game_over_bool
\prg_generate_conditional_variant:Nnn \tl_if_eq:nn { xx } { F }
% #1: integer denotation for the number to test
\prg_new_protected_conditional:Npnn \sociv_is_palindrome:n #1 { T, F, TF }
{
\int_set:Nn \l__sociv_ispal_current_index_int { 1 }
\int_set:Nn \l__sociv_ispal_last_index_int
{ \int_div_truncate:nn { \tl_count:n {#1} } { 2 } }
\bool_set_false:N \l__sociv_ispal_game_over_bool
\bool_until_do:nn
{
\bool_lazy_or_p:nn
{
\int_compare_p:nNn { \l__sociv_ispal_current_index_int } >
{ \l__sociv_ispal_last_index_int }
}
{ \l__sociv_ispal_game_over_bool }
}
{
\tl_if_eq:xxF
{ \tl_item:nn {#1} { \l__sociv_ispal_current_index_int } }
{ \tl_item:nn {#1} { -\l__sociv_ispal_current_index_int } }
{ \bool_set_true:N \l__sociv_ispal_game_over_bool }
\int_incr:N \l__sociv_ispal_current_index_int
}
\bool_if:NTF \l__sociv_ispal_game_over_bool
{ \prg_return_false: }
{ \prg_return_true: }
}
\prg_generate_conditional_variant:Nnn \sociv_is_palindrome:n { V } { T, F, TF }
\int_new:N \l__sociv_flpp_start_of_range_int
\int_new:N \l__sociv_flpp_end_of_range_int
\int_new:N \l__sociv_flpp_product_int % tested product in the inner loop
% These vars will hold data corresponding to the greatest product found so far
\tl_new:N \l__sociv_flpp_greatest_product_so_far_tl
\tl_new:N \l__sociv_flpp_first_factor_tl
\tl_new:N \l__sociv_flpp_second_factor_tl
% #1: tl var where the first factor will be stored
% #2: tl var where the second factor will be stored
% #3: tl var where the greatest product will be stored
% #4: number of digits in each factor to test (leading zeros excluded)
\cs_new_protected:Npn \sociv_find_largest_palindrome_product:NNNn #1#2#3#4
{
\tl_set:Nn \l__sociv_flpp_greatest_product_so_far_tl { 0 }
\tl_set:Nn \l__sociv_flpp_first_factor_tl { 0 }
\tl_set:Nn \l__sociv_flpp_second_factor_tl { 0 }
\int_set:Nn \l_tmpa_int {#4} % evaluate this ⟨integer expression⟩ once
% \prg_replicate:nn is used to efficiently compute powers of ten
\int_set:Nn \l__sociv_flpp_start_of_range_int
{ 1 \prg_replicate:nn { \l_tmpa_int - 1 } { 0 } }
\int_set:Nn \l__sociv_flpp_end_of_range_int
{ 1 \prg_replicate:nn { \l_tmpa_int } { 0 } - 1 }
\int_step_inline:nnn { \l__sociv_flpp_start_of_range_int }
{ \l__sociv_flpp_end_of_range_int }
{
\int_compare:nNnF { \int_mod:nn {##1} { 10 } } = { 0 }
{
\int_step_inline:nnn { \l__sociv_flpp_start_of_range_int } {##1}
{
\int_compare:nNnF { \int_mod:nn {####1} { 10 } } = { 0 }
{
\int_set:Nn \l__sociv_flpp_product_int { ##1 * ####1 }
\sociv_is_palindrome:VT \l__sociv_flpp_product_int
{
\int_compare:nNnT
{ \l__sociv_flpp_product_int } >
{ \l__sociv_flpp_greatest_product_so_far_tl }
{
\tl_set:Nn \l__sociv_flpp_first_factor_tl {##1}
\tl_set:Nn \l__sociv_flpp_second_factor_tl {####1}
\tl_set:NV \l__sociv_flpp_greatest_product_so_far_tl
\l__sociv_flpp_product_int
}
}
}
}
}
}
\tl_set_eq:NN #1 \l__sociv_flpp_second_factor_tl
\tl_set_eq:NN #2 \l__sociv_flpp_first_factor_tl
\tl_set_eq:NN #3 \l__sociv_flpp_greatest_product_so_far_tl
}
\cs_new_eq:NN \findLargestPalindromeProduct
\sociv_find_largest_palindrome_product:NNNn
\cs_new_eq:NN \clistMapInline \clist_map_inline:nn
\ExplSyntaxOff
\begin{document}
\clistMapInline{1, 2, 3}{%
\findLargestPalindromeProduct{\firstFactor}{\secondFactor}{\maxProduct}{#1}%
$\firstFactor \times \secondFactor = \maxProduct$\par
}
\end{document}
```
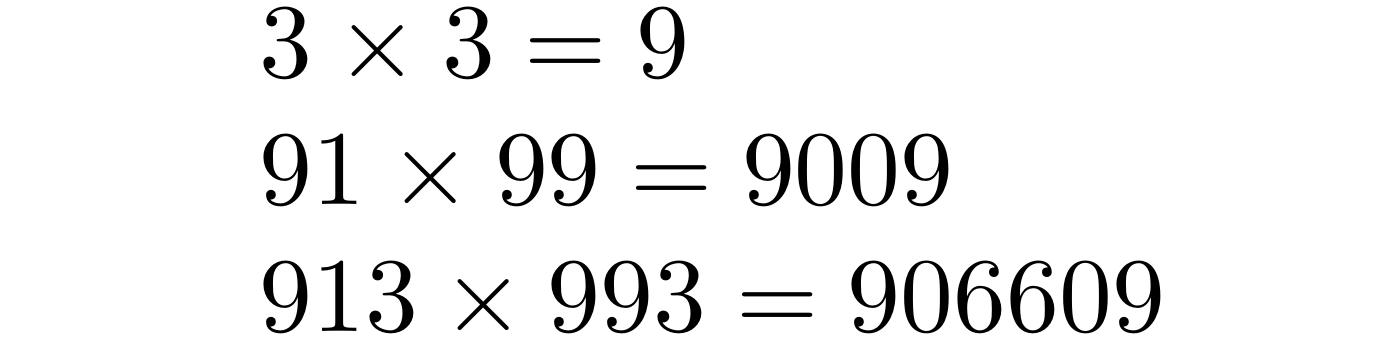
# A better optimization (samcarter's idea)
In this section, I steal samcarter's excellent [idea](https://topanswers.xyz/tex?q=2082#a2321) of comparing a `tl` var to its reverse in order to test whether it is a palindrome. This makes the `\sociv_is_palindrome:nTF` conditional *much* easier to write and significantly faster. I've tested two implementations; the second one is slightly faster (`\tl_reverse_items:n` appears to be optimized for speed).
## First implementation
The conditional is not expandable because `\tl_if_eq:nnTF` isn't itself expandable (contrary to `\tl_if_eq:NNTF`); hence the `protected`.
```
\prg_generate_conditional_variant:Nnn \tl_if_eq:nn { e } { TF }
\prg_new_protected_conditional:Npnn \sociv_is_palindrome:n #1 { T, F, TF }
{
\tl_if_eq:enTF { \tl_reverse:n {#1} } {#1}
{ \prg_return_true: }
{ \prg_return_false: }
}
```
## Second implementation
This one isn't expandable either. First because `\tl_if_eq:NnTF` isn't expandable, and second because I use non-expandable operations in order to prepare `\l__sociv_is_palindrome_tmp_tl` as a copy of the first argument with each item wrapped inside braces (I do this because `\tl_reverse_items:n` wraps items of its result within braces if they weren't already braced).
```
\tl_new:N \l__sociv_is_palindrome_tmp_tl
\prg_generate_conditional_variant:Nnn \tl_if_eq:Nn { Nx } { TF }
\prg_new_protected_conditional:Npnn \sociv_is_palindrome:n #1 { T, F, TF }
{
\tl_clear:N \l__sociv_is_palindrome_tmp_tl
\tl_map_inline:nn {#1}
{ \tl_put_right:Nn \l__sociv_is_palindrome_tmp_tl { {##1} } }
\tl_if_eq:NxTF \l__sociv_is_palindrome_tmp_tl { \tl_reverse_items:n {#1} }
{ \prg_return_true: }
{ \prg_return_false: }
}
```
## Full code with the second implementation
```
\documentclass{article}
\ExplSyntaxOn
\int_new:N \l__sociv_ispal_current_index_int
\int_new:N \l__sociv_ispal_last_index_int
\bool_new:N \l__sociv_ispal_game_over_bool
\tl_new:N \l__sociv_is_palindrome_tmp_tl
\prg_generate_conditional_variant:Nnn \tl_if_eq:Nn { Nx } { TF }
% #1: integer denotation for the number to test
\prg_new_protected_conditional:Npnn \sociv_is_palindrome:n #1 { T, F, TF }
{
\tl_clear:N \l__sociv_is_palindrome_tmp_tl
\tl_map_inline:nn {#1}
{ \tl_put_right:Nn \l__sociv_is_palindrome_tmp_tl { {##1} } }
\tl_if_eq:NxTF \l__sociv_is_palindrome_tmp_tl { \tl_reverse_items:n {#1} }
{ \prg_return_true: }
{ \prg_return_false: }
}
\prg_generate_conditional_variant:Nnn \sociv_is_palindrome:n { V } { T, F, TF }
\int_new:N \l__sociv_flpp_start_of_range_int
\int_new:N \l__sociv_flpp_end_of_range_int
\int_new:N \l__sociv_flpp_product_int % tested product in the inner loop
% These vars will hold data corresponding to the greatest product found so far
\tl_new:N \l__sociv_flpp_greatest_product_so_far_tl
\tl_new:N \l__sociv_flpp_first_factor_tl
\tl_new:N \l__sociv_flpp_second_factor_tl
% #1: tl var where the first factor will be stored
% #2: tl var where the second factor will be stored
% #3: tl var where the greatest product will be stored
% #4: number of digits in each factor to test (leading zeros excluded)
\cs_new_protected:Npn \sociv_find_largest_palindrome_product:NNNn #1#2#3#4
{
\tl_set:Nn \l__sociv_flpp_greatest_product_so_far_tl { 0 }
\tl_set:Nn \l__sociv_flpp_first_factor_tl { 0 }
\tl_set:Nn \l__sociv_flpp_second_factor_tl { 0 }
\int_set:Nn \l_tmpa_int {#4} % evaluate this ⟨integer expression⟩ once
% \prg_replicate:nn is used to efficiently compute powers of ten
\int_set:Nn \l__sociv_flpp_start_of_range_int
{ 1 \prg_replicate:nn { \l_tmpa_int - 1 } { 0 } }
\int_set:Nn \l__sociv_flpp_end_of_range_int
{ 1 \prg_replicate:nn { \l_tmpa_int } { 0 } - 1 }
\int_step_inline:nnn { \l__sociv_flpp_start_of_range_int }
{ \l__sociv_flpp_end_of_range_int }
{
\int_compare:nNnF { \int_mod:nn {##1} { 10 } } = { 0 }
{
\int_step_inline:nnn { \l__sociv_flpp_start_of_range_int } {##1}
{
\int_compare:nNnF { \int_mod:nn {####1} { 10 } } = { 0 }
{
\int_set:Nn \l__sociv_flpp_product_int { ##1 * ####1 }
\sociv_is_palindrome:VT \l__sociv_flpp_product_int
{
\int_compare:nNnT
{ \l__sociv_flpp_product_int } >
{ \l__sociv_flpp_greatest_product_so_far_tl }
{
\tl_set:Nn \l__sociv_flpp_first_factor_tl {##1}
\tl_set:Nn \l__sociv_flpp_second_factor_tl {####1}
\tl_set:NV \l__sociv_flpp_greatest_product_so_far_tl
\l__sociv_flpp_product_int
}
}
}
}
}
}
\tl_set_eq:NN #1 \l__sociv_flpp_second_factor_tl
\tl_set_eq:NN #2 \l__sociv_flpp_first_factor_tl
\tl_set_eq:NN #3 \l__sociv_flpp_greatest_product_so_far_tl
}
\cs_new_eq:NN \findLargestPalindromeProduct
\sociv_find_largest_palindrome_product:NNNn
\cs_new_eq:NN \clistMapInline \clist_map_inline:nn
\ExplSyntaxOff
\begin{document}
\clistMapInline{1, 2, 3}{%
\findLargestPalindromeProduct{\firstFactor}{\secondFactor}{\maxProduct}{#1}%
$\firstFactor \times \secondFactor = \maxProduct$\par
}
\end{document}
```
Same output as above.
Answer #2
samcarter

*no spoiler here*
Not very efficient, but I learnt about `\tl_reverse:V`:
```
\documentclass{article}
\begin{document}
A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is $9009 = 91 \times 99$.
Find the largest palindrome made from the product of two 3-digit numbers.
\ExplSyntaxOn
\int_new:N \l_sam_a_int
\int_new:N \l_sam_b_int
\int_new:N \l_sam_prod_int
\int_new:N \l_sam_pali_int
\tl_new:N \l_sam_prod_tl
\tl_new:N \l_sam_rev_tl
% loop over a
\int_step_inline:nnn {100} {999}
{
\int_set:Nn \l_sam_a_int { #1 }
% loop over b
\int_step_inline:nnn {100} {\l_sam_a_int}
{
\int_set:Nn \l_sam_b_int { ##1 }
% calculating product
\int_set:Nn \l_sam_prod_int { \l_sam_a_int * \l_sam_b_int }
% make a token list from the product
\tl_set:NV \l_sam_prod_tl \l_sam_prod_int
% reverse the token list
\tl_set:Nx \l_sam_rev_tl { \tl_reverse:V \l_sam_prod_tl }
% compare origional and reverse token list
\tl_if_eq:NNT \l_sam_prod_tl \l_sam_rev_tl
{
% check if palindrom is the largest
\int_compare:nNnT { \l_sam_pali_int } < { \l_sam_prod_int }
{
\int_set_eq:NN \l_sam_pali_int \l_sam_prod_int
}
}
}
}
\par
\int_use:N \l_sam_pali_int
\ExplSyntaxOff
\end{document}
```