samcarter

> This is part of the Summer of Code 2022 series, see https://topanswers.xyz/tex?q=2059 for more information
A Pythagorean triplet is a set of three natural numbers, a < b < c, for which, a^2^ + b^2^ = c^2^
For example, 3^2^ + 4^2^ = 9 + 16 = 25 = 5^2^.
There exists exactly one Pythagorean triplet for which a + b + c = 1000. Find this triplet and calculate the product a × b × c.
(this programming puzzle is taken from https://projecteuler.net/problem=9, licensed under CC BY-NC-SA 4.0)

Top Answer
frougon

\* This line is not a spoiler. \*
I decided to call “goal” the desired value for a + b + c and:
* work with an arbitrary goal (make sure it is not too large for TeX arithmetic);
* avoid possible “misses” due to rounded division results (there is no division in my code; see the tests used in the conditions of each `\bool_while_do:nn` loop; no `\int_step_inline:nnn` here on purpose);
* print all solutions with 0 < a < b < c for the specified goal;
* make the printing user-parametrizable using code where `#1`, `#2` and `#3` are replaced with the a, b, c values found every time a triplet fulfills the conditions 0 < a < b < c, a + b + c = *goal* and a² + b² = c².
We use a little shortcut to avoid trying all possible combinations for *a* and *b*: under the stated conditions, 3*a* < *a* + *b* + *c* and 2*b* < *b* + *c* < *a* + *b* + *c*.
Edit: as Skillmon [wrote](https://topanswers.xyz/transcript?room=2123&id=142100#c142100), the first condition can be made tighter: since a + 1 ≤ b and b + 1 ≤ c, a + b + 2 ≤ b + c, thus 2a + 3 ≤ b + c, 3a + 3 ≤ a + b + c and finally 3a + 2 < a + b + c. Similarly, for the second condition: b < c, therefore 2b < b + c, which leads to a + 2b < a + b + c.
```
\documentclass[twocolumn]{article}
\usepackage[paperwidth=25cm,paperheight=13.5cm]{geometry} % for the screenshot
% \usepackage{xfp} % uncomment if your LaTeX is older than June 2022
\usepackage{siunitx}
\ExplSyntaxOn
\int_new:N \l__soci_find_triplets_a_int
\int_new:N \l__soci_find_triplets_b_int
\int_new:N \l__soci_find_triplets_c_int
\int_new:N \l__soci_find_triplets_goal_int
% #1: seq variable where good triplets are stored (it is cleared when starting)
% #2: goal for a + b + c
\cs_new_protected:Npn \soci_find_triplets:Nn #1#2
{
\seq_clear:N #1
\int_set:Nn \l__soci_find_triplets_goal_int {#2} % compute only once
\int_set:Nn \l__soci_find_triplets_a_int { 1 }
\bool_while_do:nn
{
\int_compare_p:nNn { 3 * \l__soci_find_triplets_a_int + 2 } <
{ \l__soci_find_triplets_goal_int }
}
{
\int_set:Nn \l__soci_find_triplets_b_int % first value for b : a + 1
{ \l__soci_find_triplets_a_int + 1 }
\bool_while_do:nn
{
\int_compare_p:nNn
{ \l__soci_find_triplets_a_int + 2 * \l__soci_find_triplets_b_int }
<
{ \l__soci_find_triplets_goal_int }
}
{
\int_set:Nn \l__soci_find_triplets_c_int
{
\l__soci_find_triplets_goal_int - \l__soci_find_triplets_a_int
- \l__soci_find_triplets_b_int
}
\int_compare:nNnT
{ \l__soci_find_triplets_a_int * \l__soci_find_triplets_a_int +
\l__soci_find_triplets_b_int * \l__soci_find_triplets_b_int }
=
{ \l__soci_find_triplets_c_int * \l__soci_find_triplets_c_int }
{ % store the triplet
\seq_put_right:Nx #1
{
\int_use:N \l__soci_find_triplets_a_int ,
\int_use:N \l__soci_find_triplets_b_int ,
\int_use:N \l__soci_find_triplets_c_int
}
}
\int_incr:N \l__soci_find_triplets_b_int
}
\int_incr:N \l__soci_find_triplets_a_int
}
}
\seq_new:N \l__sdftws_solutions_seq
\tl_new:N \l__sdftws_a_tl
\tl_new:N \l__sdftws_b_tl
\tl_new:N \l__sdftws_c_tl
\tl_new:N \l__sdftws_output_tl
\cs_new:Npn \__sdftws_print_one_solution:nnn #1#2#3 { }
% #1: goal for a + b + c
% #2: code used for printing each solution (with a, b, c substituted for #1, #2
% and #3)
\cs_new_protected:Npn \soci_do_for_triplets_with_sum:nn #1#2
{
% Define a macro with the user-provided code as replacement text
\cs_set:Npn \__sdftws_print_one_solution:nnn ##1##2##3 {#2}
\soci_find_triplets:Nn \l__sdftws_solutions_seq {#1}
% Useful to find goals with several solutions
\int_compare:nNnT { \seq_count:N \l__sdftws_solutions_seq } > { 1 }
{
\iow_term:x { \seq_count:N \l__sdftws_solutions_seq \c_space_tl
solutions~ for~ goal~ #1. }
}
\tl_clear:N \l__sdftws_output_tl
\seq_map_inline:Nn \l__sdftws_solutions_seq
{
\seq_set_from_clist:Nn \l_tmpa_seq {##1}
\seq_pop_left:NN \l_tmpa_seq \l__sdftws_a_tl % store value of a
\seq_pop_left:NN \l_tmpa_seq \l__sdftws_b_tl % store value of b
\seq_pop_left:NN \l_tmpa_seq \l__sdftws_c_tl % store value of c
\tl_set:Nx \l_tmpa_tl
{
\exp_not:N \__sdftws_print_one_solution:nnn
{ \l__sdftws_a_tl } { \l__sdftws_b_tl } { \l__sdftws_c_tl }
}
\exp_args:NNV
\tl_put_right:No \l__sdftws_output_tl \l_tmpa_tl
}
\tl_use:N \l__sdftws_output_tl
}
\cs_new_eq:NN \doForTripletsWithSum \soci_do_for_triplets_with_sum:nn
\cs_new_eq:NN \clistMapInline \clist_map_inline:nn
% Useful to find goals with several solutions
% \int_step_inline:nn { 2000 } { \soci_do_for_triplets_with_sum:nn {#1} { } }
\ExplSyntaxOff
\newcommand*{\printOne}[1]{%
\noindent $
\begin{array}{@{} cccr @{}}
(a, b, c) & a + b + c & a^2 + b^2 - c^2 & \multicolumn{1}{c}{abc}
\\[0.2ex]
% This produces one row for each solution
\doForTripletsWithSum{#1}{%
(##1, ##2, ##3) &
\num{\fpeval{##1 + ##2 + ##3}} &
\num{\fpeval{##1^2 + ##2^2 - ##3^2}} &
\num{\fpeval{##1 * ##2 * ##3}} \\
}
\end{array}$\par\bigskip
}
\pagestyle{empty}
\begin{document}
\clistMapInline{1000, 60, 84, 252, 360, 420, 720, 2880}{\printOne{#1}}
\end{document}
```

Answer #2
Skillmon

ASCII-duck wants to solve:
The following implements a rather simple minded loop to find a Pythagorean triplet with a given sum and returns three braced groups holding the first found triplet. If no triplet with the given sum is found an error is thrown and `{-1}{-1}{-1}` is left in the input stream.
The conditions *a* < *b* < *c* are enforced (the `\ifnum` tests and the fact that the inner loop iterating *b* is always started with *a* + 1).
The Pythagorean triplet condition is checked by the `\if0`-check (`\if0` is faster than `\ifnum` for equal to 0 checks -- but `\if` can't be used to check for negative or positive numbers, hence the other checks use `\ifnum`).
```
\documentclass{article}
\usepackage{ducksay}% remember who wants to solve
\usepackage{expkv}% only for ekverr
\makeatletter
\def\pythagoreantriplet#1%
{%
\expandafter\pythagoreantriplet@a
\the\numexpr#1\expandafter;%
\the\numexpr2*(#1)\expandafter;%
\the\numexpr(#1)*(#1)\relax;%
}
\def\pythagoreantriplet@a
#1;% sum
#2;% 2*sum
#3;% sum^2
{%
\pythagoreantriplet@b1;{#1}{#2}{#3}\pythagoreantriplet@mark}
\def\pythagoreantriplet@b
#1;% a
#2% sum
#3% 2*sum
#4% sum^2
{%
\ifnum\the\numexpr3*#1+3\relax>#2
\pythagoreantriplet@error
\fi
\expandafter\pythagoreantriplet@c\the\numexpr#1+1\relax;{#1}{#2}{#3}{#4}%
}
\def\pythagoreantriplet@c
#1;% b
#2% a
#3% sum
#4% 2*sum
#5% sum^2
{%
\ifnum\the\numexpr#3-#2-#1\relax>#1
\else
\pythagoreantriplet@next
\fi
% 0 == a^2 + b^2 - (#3 - a - b)^2
% = 2*#3*(a + b) - 2*a*b - #3^2
\if0\the\numexpr#4*(#1+#2)-2*#1*#2-#5\relax
\expandafter\pythagoreantriplet@done\the\numexpr#3-#2-#1\relax;{#1}{#2}%
\fi
\expandafter\pythagoreantriplet@c\the\numexpr#1+1\relax;{#2}{#3}{#4}{#5}%
}
\def\pythagoreantriplet@done
#1;% c
#2% b
#3% a
#4\pythagoreantriplet@mark% junk
{\fi{#3}{#2}{#1}}
\def\pythagoreantriplet@next
\fi#1\fi#2;% junk
#3% current outer loop
{\fi\expandafter\pythagoreantriplet@b\the\numexpr#3+1\relax;}
\def\pythagoreantriplet@error\fi#1;#2#3#4\pythagoreantriplet@mark
{\fi\ekverr{pythagorean}{sum #3 not satisfiable}{-1}{-1}{-1}}
\makeatother
\def\solveSoC{\expanded{\prettyprint\pythagoreantriplet{1000}}}
\protected\def\prettyprint#1#2#3%
{%
\duckthink[vpad=1,msg*={}]
{%
$#1+#2+#3=\inteval{#1+#2+#3}$\\
$#1^2+#2^2=\inteval{#1*#1+#2*#2}=\inteval{#3*#3}=#3^2$
}\par
\ducksay[vpad=1,msg*={}]
{The answer is: $\inteval{#1*#2*#3}$}%
}
\begin{document}
\solveSoC
\end{document}
```
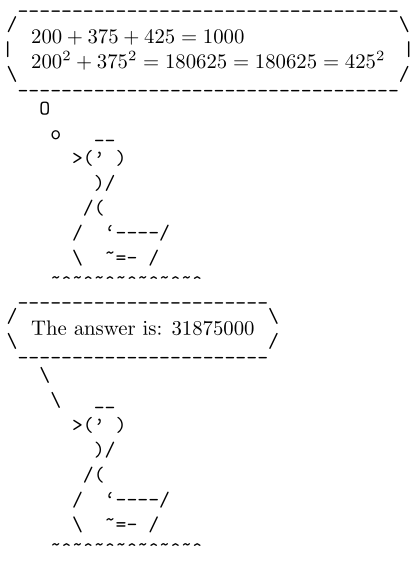
Another (but pretty similar) implementation, this one should be faster on average by choosing better start values for *a* and *b* (for both the biggest possible value is chosen as the start value). This results in different results if multiple Pythagorean triplets are possible for the same sum (first code yields the solution with the smallest *a* and hence smallest product, this one the one with the biggest *a*/product). This also simplifies the end-of-loop tests for both *a* and *b* (just check *a* ≠ 0 for the outer and *b* ≠ *a* for the inner loop). Additionally I changed the return value in error cases to 0.
```
\documentclass{article}
\usepackage{ducksay}% remember who wants to solve
\usepackage{expkv}% only for ekverr
\makeatletter
\def\pythagoreantriplet#1%
{%
\expandafter\pythagoreantriplet@a
% -3 because of 3a+3 <= sum, another -1 to get truncating division
\the\numexpr#1-4\expandafter;%
\the\numexpr#1\expandafter;%
\the\numexpr2*(#1)\expandafter;%
\the\numexpr(#1)*(#1)\relax;%
}
\def\pythagoreantriplet@a
#1#2;% sum-4
#3;% sum
#4;% 2*sum
#5;% sum^2
{%
\ifx-#1\pythagoreantriplet@error#3\fi
\expandafter\pythagoreantriplet@b\the\numexpr#1#2/3\relax;%
{#3}{#4}{#5}\pythagoreantriplet@mark
}
\def\pythagoreantriplet@b
#1;% a
#2% sum
{%
\ifx0#1\pythagoreantriplet@error#2\fi
% -1 because 2b+1 <= sum-a, another -1 to get truncating division
\expandafter\pythagoreantriplet@c\the\numexpr(#2-#1-2)/2\relax;{#1}{#2}
}
\def\pythagoreantriplet@c
#1;% b
#2% a
#3% sum
#4% 2*sum
#5% sum^2
{%
\ifnum#1=#2 \pythagoreantriplet@next\fi
% 0 == a^2 + b^2 - (sum - a - b)^2
% = 2*sum*(a + b) - 2*a*b - sum^2
\if0\the\numexpr#4*(#1+#2)-2*#1*#2-#5\relax
\expandafter\pythagoreantriplet@done\the\numexpr#3-#2-#1\relax;{#1}{#2}%
\fi
\expandafter\pythagoreantriplet@c\the\numexpr#1-1\relax;{#2}{#3}{#4}{#5}%
}
\def\pythagoreantriplet@done
#1;% c
#2% b
#3% a
#4\pythagoreantriplet@mark% junk
{\fi{#3}{#2}{#1}}
\def\pythagoreantriplet@next
\fi#1\fi#2;% junk
#3% current a-loop
{\fi\expandafter\pythagoreantriplet@b\the\numexpr#3-1\relax;}
\def\pythagoreantriplet@error#1\fi#2\pythagoreantriplet@mark
{%
\fi
\ekverr{pythagorean}{sum #1 not satisfiable}
000%
}
\makeatother
\def\solveSoC{\expanded{\prettyprint\pythagoreantriplet{1000}}}
\protected\def\prettyprint#1#2#3%
{%
\duckthink[vpad=1,msg*={}]
{%
$#1+#2+#3=\inteval{#1+#2+#3}$\\
$#1^2+#2^2=\inteval{#1*#1+#2*#2}=\inteval{#3*#3}=#3^2$
}\par
\ducksay[vpad=1,msg*={}]
{The answer is: $\inteval{#1*#2*#3}$}%
}
\begin{document}
\solveSoC
\end{document}
```
Answer #3
samcarter

*no spoiler to be seen*
So, not efficient at all, just the brute force approach to loop over a and b, then calculate c and check if it meets the a+b+c=1000 criterium:
```
\documentclass{article}
\begin{document}
A Pythagorean triplet is a set of three natural numbers, $a < b < c$, for which, $a^2 + b^2 = c^2$
For example, $3^2 + 4^2 = 9 + 16 = 25 = 5^2$.
There exists exactly one Pythagorean triplet for which $a + b + c = 1000$. Find this triplet and calculate the product $a \times b \times c$.
\ExplSyntaxOn
\int_new:N \l_sam_a_int
\int_new:N \l_sam_asquare_int
\int_new:N \l_sam_b_int
\int_new:N \l_sam_bsquare_int
\fp_new:N \l_sam_c_fp
\int_new:N \l_sam_c_int
\int_new:N \l_sam_csquare_int
% loop over b (next biggest integer)
\int_step_variable:nNn {400} \l_sam_b_int {
% storing b square
\int_set:Nn \l_sam_bsquare_int {
\l_sam_b_int*\l_sam_b_int
}
% loop over a (smalles integer)
\int_step_variable:nNn {\l_sam_b_int-1} \l_sam_a_int {
% storing a square
\int_set:Nn \l_sam_asquare_int {
\l_sam_a_int*\l_sam_a_int
}
% calculating csquare
\int_set:Nn \l_sam_csquare_int {
\l_sam_asquare_int + \l_sam_bsquare_int
}
% calculating c
\fp_set:Nn \l_sam_c_fp {
\fp_eval:n {sqrt(\l_sam_csquare_int)}
}
% check if c integer
\fp_compare:nTF{0.0001 < abs(round(\l_sam_c_fp)-\l_sam_c_fp)}{}{
% get an integer version of c
\int_set:Nn \l_sam_c_int {
\fp_to_int:n { \l_sam_c_fp }
}
% check of sum is 100
\int_compare:nNnTF { \int_eval:n {\l_sam_c_int}+\l_sam_b_int+\l_sam_a_int } = { 1000 }{
\par
a=\l_sam_a_int\space
b=\l_sam_b_int\space
c=\int_eval:n {\l_sam_c_int}
\par
$a + b + c = \int_eval:n {\l_sam_a_int + \l_sam_b_int + \int_eval:n {\l_sam_c_int}}$
\par
$a \times b \times c = \int_eval:n {\l_sam_a_int * \l_sam_b_int * \int_eval:n {\l_sam_c_int}}$
}{}% check if 1000
}% check c integer
}% loop a
}% loop b
\ExplSyntaxOff
\end{document}
```

----
Quite a bit faster:
Check first if the a+b+c=1000 criterium is met before calculating c and the product
```
\documentclass{article}
\begin{document}
A Pythagorean triplet is a set of three natural numbers, $a < b < c$, for which, $a^2 + b^2 = c^2$
For example, $3^2 + 4^2 = 9 + 16 = 25 = 5^2$.
There exists exactly one Pythagorean triplet for which $a + b + c = 1000$. Find this triplet and calculate the product $a \times b \times c$.
\ExplSyntaxOn
\int_new:N \l_sam_a_int
\int_new:N \l_sam_b_int
\int_new:N \l_sam_c_int
% loop over b (next biggest integer)
\int_step_inline:nn {1000}
{
\int_set:Nn \l_sam_b_int { #1 }
% loop over a (smalles integer)
\int_step_inline:nn {\l_sam_b_int-1}
{
\int_set:Nn \l_sam_a_int { ##1 }
% check if a^2 + b^2 = (1000 - a - b)^2
\int_compare:nNnT
{
\l_sam_b_int*\l_sam_b_int + \l_sam_a_int*\l_sam_a_int
} = {
(1000-\l_sam_a_int-\l_sam_b_int)*(1000-\l_sam_a_int-\l_sam_b_int)
}{
% calculating c
\int_set:Nn \l_sam_c_int
{
1000 - \l_sam_b_int - \l_sam_a_int
}
a=\int_use:N \l_sam_a_int\space
b=\int_use:N \l_sam_b_int\space
c=\int_use:N \l_sam_c_int
\par
$a + b + c = \int_eval:n {\l_sam_a_int + \l_sam_b_int + \l_sam_c_int}$
\par
$a \times b \times c = \int_eval:n {\l_sam_a_int * \l_sam_b_int * \l_sam_c_int}$
}% if a^2 + b^2 = (1000 - a - b)^2
}% loop a
}% loop b
\ExplSyntaxOff
\end{document}
```