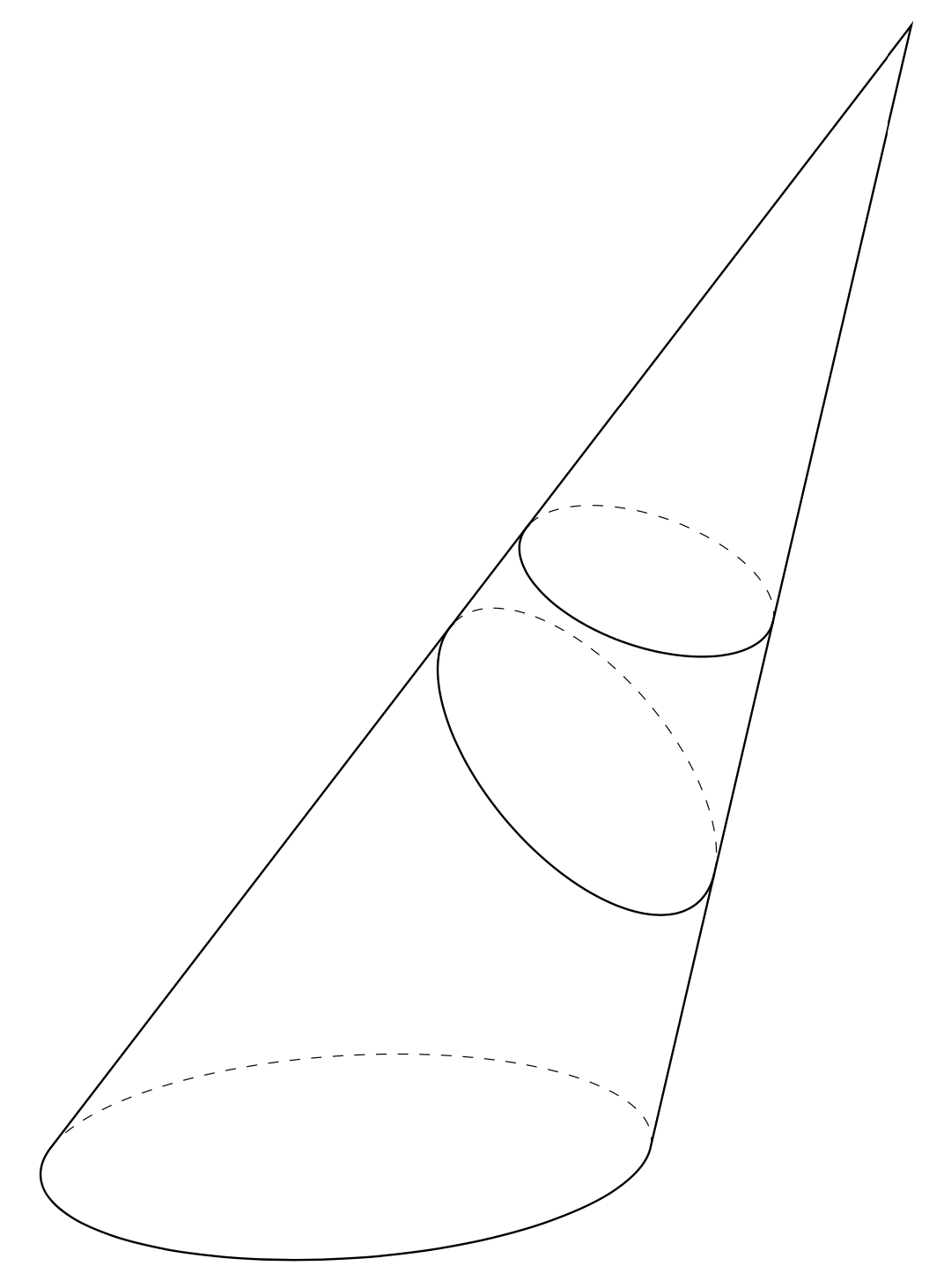
You can use the [conical sections](https://topanswers.xyz/tex?q=1546#a1803) along with `xslant`.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\makeatletter
\tikzset{pics/3d/intersection of cone with plane/.style={code={
\def\pv##1{\pgfkeysvalueof{/tikz/3d/intersection of cone with plane/##1}}
\tikzset{declare function={%
iconeplaneradius(\x,\y,\z)=\z/(1+\y*cos(\x));% https://tex.stackexchange.com/a/457458
iconeplaneh(\x)=\pv{h}*(\pv{r}-\x)/\pv{r};
},
3d/intersection of cone with plane/.cd,#1,
e/.evaluated={cos(90+\pv{alpha})/cos(\pv{beta})},
s/.evaluated={(1+\pv{e})*\pv{r}*(\pv{h}-\pv{Iz})/(\pv{h}*sin(90+\pv{alpha}))},
beta/.evaluated={atan2(\pv{r},\pv{h})}}
\pgfmathtruncatemacro{\itest}{(\pv{e}<0.1?0:1)}
\ifnum\itest=0\relax
\pgfmathsetmacro{\tcrit}{180}
\else
\pgfmathsetmacro{\tmp}{(\pv{s}-\pv{r})/(\pv{r}*\pv{e})}
\pgfmathtruncatemacro{\itest}{(abs(\tmp)<1?1:0)}
\ifnum\itest=1
\pgfmathsetmacro{\tcrit}{abs(acos(\tmp))}
%\typeout{tcrit=\tcrit}
\else
\pgfmathsetmacro{\tcrit}{180}
\fi
\fi
% warning: this may only work for psi=0
\pgfmathsetmacro{\myphi}{atan2(\pgf@yx,\pgf@xx)}
\pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})}
\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))}
\pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})}
\pgfmathsetmacro{\tvis}{90-\alphacrit+\myphi+\pv{gamma}}
%\typeout{alpha_crit=\alphacrit, phi=\myphi, t_vis=\tvis}
\path[pic actions] plot[variable=\t,domain=-\tcrit:\tcrit,samples=101,smooth]
({iconeplaneradius(\t,\pv{e},\pv{s})*cos(\t-\pv{gamma})},
{iconeplaneradius(\t,\pv{e},\pv{s}))*sin(\t-\pv{gamma})},
{iconeplaneh(iconeplaneradius(\t,\pv{e},\pv{s}))});
\pgfmathtruncatemacro{\isamples}{50*abs(\tcrit-\tvis)/abs(\tcrit)+1}
\draw[3d/hidden] plot[variable=\t,domain=\tcrit:\tvis,samples=\isamples,smooth]
({iconeplaneradius(\t,\pv{e},\pv{s})*cos(\t-\pv{gamma})},
{iconeplaneradius(\t,\pv{e},\pv{s}))*sin(\t-\pv{gamma})},
{iconeplaneh(iconeplaneradius(\t,\pv{e},\pv{s}))});
\pgfmathtruncatemacro{\isamples}{50*abs(\tcrit+\tvis)/abs(\tcrit)+1}
\draw[3d/visible] plot[variable=\t,domain=-\tcrit:\tvis,samples=\isamples,smooth]
({iconeplaneradius(\t,\pv{e},\pv{s})*cos(\t-\pv{gamma})},
{iconeplaneradius(\t,\pv{e},\pv{s}))*sin(\t-\pv{gamma})},
{iconeplaneh(iconeplaneradius(\t,\pv{e},\pv{s}))});
}},/tikz/3d/intersection of cone with plane/.cd,
h/.initial=5,% height of the cone
r/.initial=3,% radius of the base
gamma/.initial=0,% angle of intersection
Iz/.initial=3,% z coordinate of the intersection
alpha/.initial=0,% slope of the plane
beta/.initial=0,% will be computed
e/.initial=1,
s/.initial=1}
\makeatother
\begin{document}
\foreach \xslant in {0.5}
{\begin{tikzpicture}
\begin{scope}[3d/install view={phi=30,theta=70},
declare function={R=2;% radius of the base of the cone
H=8;% height of the cone
r=R/2;% radius of the small circle
h=(R-r)*H/R;% height of the base of the upper circle
},xslant=\xslant]
\path
(0,0,0) coordinate (O) % center of base of the cone (fixed)
(0,0,H) coordinate (T); % tip of the cone
%
\path (O) pic[transform shape]{3d/cone={r=R,h=H}};
%
\begin{scope}[3d/intersection of cone with plane/.cd,r=R,h=H,gamma=-20,
/tikz/fill opacity=0.3]
\path pic[transform shape]{3d/intersection of cone with plane={%
Iz=2,alpha=10}};
\path pic[transform shape]{3d/intersection of cone with plane={%
Iz=3.75,alpha=5}};
\end{scope}
\end{scope}
\end{tikzpicture}}
\end{document}
```