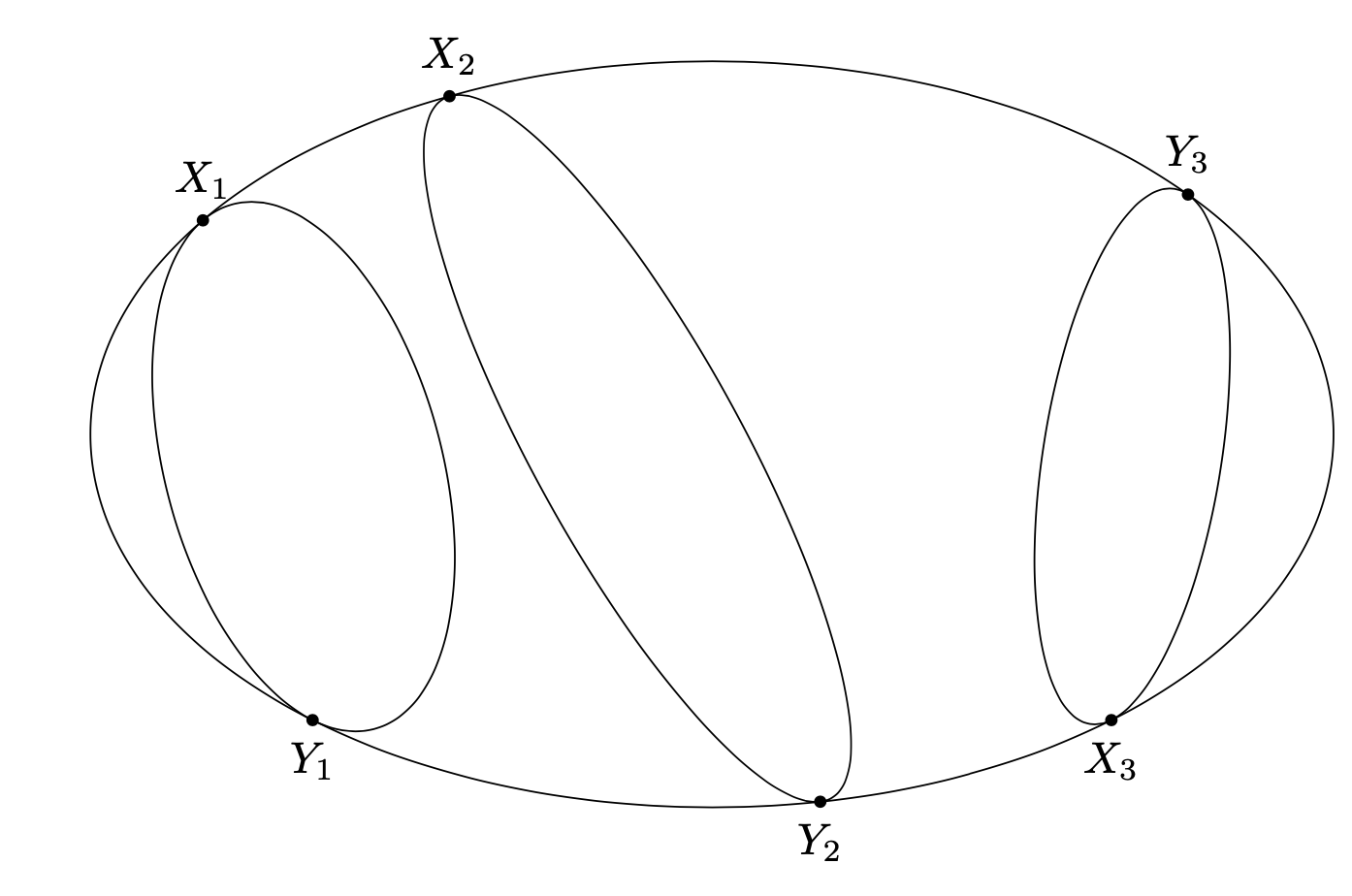
This is some sort of an answer. There is an arguably more elegant piece, which is based on
[this article](https://forumgeom.fau.edu/FG2010volume10/FG201016.pdf) to construct the inscribed ellipses via some "ruler and compass" procedure. The steps can be found in the second code block and the animation below. And then there is an uglier part in which the tangents get constructed iteratively from some reasonable but not tuned initial points on the ellipses. Technically this answers the question how to draw such a figure, but obviously there are more elegant methods. I am certainly missing some possibilities, and other possibilities are hard to implement in LaTeX, at least for me. I am posting this also because it has some other ingredients that may be useful for other application such as the computation of barycentric coordinates from Cartesian ones. Please note that you cannot put the touching points at absolutely arbitrary locations because of the `dimension too large` errors that one may encounter using the `calc` library (or more generally Ti*k*Z or LaTeX).
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}%
\begin{document}
\begin{tikzpicture}[line join = round, line cap = round,>=stealth,
c/.style={circle,fill,inner sep=1pt},
gset/.code 2 args={\expandafter\xdef\csname tikz@global@junk@#1\endcsname{#2}},
declare function={a=5;b=3;
alpha1=145;beta1=230;x1=0.4;y1=0.6;
alpha2=115;beta2=280;x2=0.02;y2=0.03;
alpha3=310;beta3=40;x3=0.2;y3=0.3;
eslope(\t)=atan2(b*cos(\t),-a*sin(\t));
Eslope(\a,\b,\t)=atan2(\b*cos(\t),-\a*sin(\t));
MassageAngle(\x)=(Mod(\x,360)<180?Mod(\x,360):Mod(\x,360)-360);
baryn(\xA,\yA,\xB,\yB,\xC,\yC)=scalar((\xA/1cm-\xC/1cm)*(\yB/1cm-\yC/1cm)-(\xB/1cm-\xC/1cm)*(\yA/1cm-\yC/1cm));
baryu(\xB,\yB,\xC,\yC,\xP,\yP)=scalar((\yB/1cm-\yC/1cm)*(\xP/1cm-\xC/1cm)+(\xC/1cm-\xB/1cm)*(\yP/1cm-\yC/1cm));
baryv(\xA,\yA,\xC,\yC,\xP,\yP)=scalar((\yC/1cm-\yA/1cm)*(\xP/1cm-\xC/1cm)+(\xA/1cm-\xC/1cm)*(\yP/1cm-\yC/1cm));
barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryu(\xB,\yB,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryv(\xA,\yA,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda3(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(1-barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)-barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP));
}]
\pgfmathdeclarefunction{gval}{1}{%
\edef\pgfmathresult{\csname tikz@global@junk@#1\endcsname}%
}%
\draw circle[x radius=a,y radius=b];
\foreach \X in {1,2,3}
{\path
(alpha\X:a and b) coordinate (aux) let \p1=(aux) in
\ifdim\y1>0pt\relax
coordinate[c,label={above:{$X_{\X}$}}] (X_\X)
\else
coordinate[c,label={below:{$X_{\X}$}}] (X_\X)
\fi
++ ({scalar(eslope(alpha\X))}:2) coordinate (aux1)
(beta\X:a and b) coordinate (aux) let \p1=(aux) in
\ifdim\y1>0pt\relax
coordinate[c,label={above:{$Y_{\X}$}}] (Y_\X)
\else
coordinate[c,label={below:{$Y_{\X}$}}] (Y_\X)
\fi
++ ({scalar(eslope(beta\X))}:2) coordinate (aux2);
\draw[overlay]
(intersection of X_\X--aux1 and Y_\X--aux2)
coordinate (C_\X)
($(X_\X)+x\X*(X_\X)-x\X*(C_\X)$) coordinate (B_\X)
($(Y_\X)+y\X*(Y_\X)-y\X*(C_\X)$) coordinate (A_\X)
(intersection of X_\X--A_\X\space and Y_\X--B_\X)
coordinate (P_\X)
($0.333*(A_\X)+0.333*(B_\X)+0.333*(C_\X)$) coordinate (O_\X)
let \p{A}=($(A_\X)-(O_\X)$),\p{B}=($(B_\X)-(O_\X)$),\p{C}=($(C_\X)-(O_\X)$),\p{P}=($(P_\X)-(O_\X)$),
\n{A}={barylambda1(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{B}={barylambda2(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{C}={barylambda3(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{u}={\n{A}*(\n{B}+\n{C})},
\n{v}={\n{B}*(\n{C}+\n{A})},
\n{w}={\n{C}*(\n{A}+\n{B})}
in
(barycentric cs:A_\X=\n{u},B_\X=\n{v},C_\X=\n{w})
coordinate (M_\X)
(intersection of B_\X--M_\X\space and A_\X--C_\X) coordinate (B_0)
(intersection of C_\X--M_\X\space and A_\X--B_\X) coordinate (C_0)
($(A_\X)+(B_0)-(B_\X)$) coordinate (auxAB)
($(A_\X)+(C_0)-(C_\X)$) coordinate (auxAC)
(intersection of A_\X--auxAB and B_\X--C_\X)
coordinate (D_\X)
(intersection of A_\X--auxAC and B_\X--C_\X)
coordinate (E_\X)
let
\p{BC}=($(C_\X)-(B_\X)$),\n{BC}={scalar(veclen(\x{BC},\y{BC})/1cm)},
\p{BD}=($(B_\X)-(D_\X)$),\n{BD}={scalar(veclen(\x{BD},\y{BD})/1cm)},
\p{CE}=($(C_\X)-(E_\X)$),\n{CE}={scalar(veclen(\x{CE},\y{CE})/1cm)},
\n{x}={(\n{BD}*\n{BD}-\n{CE}*\n{CE}+\n{BC}*\n{BC})/2/\n{BC}},
\n{y}={sqrt(\n{BD}*\n{BD}-\n{x}*\n{x})},
\n{phi}={scalar(atan2(\y{BC},\x{BC}))}
in ($(B_\X)+(\n{phi}:\n{x})+(\n{phi}+90:\n{y})$) coordinate (Ap)
($(B_\X)+(\n{phi}:\n{x})+(\n{phi}-90:\n{y})$) coordinate (Am)
let \p1=($(Ap)-(A_\X)$),\p2=($(Am)-(A_\X)$),
\n1={veclen(\x2,\y2)-veclen(\x1,\y1)} in
\ifdim\n1>0pt\relax
(Ap) coordinate (Ap)
(Am) coordinate (Am)
\else
(Am) coordinate (Ap)
(Ap) coordinate (Am)
\fi
let \p{p}=($(Ap)-(A_\X)$),\p{m}=($(Am)-(A_\X)$),
\n{bis}={scalar(0.5*atan2(\y{p},\x{p})+0.5*atan2(\y{m},\x{m}))}
in ($(A_\X)+(\n{bis}:2)$) coordinate (Abis)
(intersection of A_\X--Abis and B_\X--C_\X)
coordinate (Q_\X)
let \p{Q}=($(Q_\X)-(A_\X)$),
\n{phi}={scalar(atan2(\y{Q},\x{Q}))}
in
let \p{Ap}=($(Ap)-(A_\X)$),\p{Am}=($(Am)-(A_\X)$),
\n{Ap}={scalar(veclen(\x{Ap},\y{Ap})/1cm)},
\n{Am}={scalar(veclen(\x{Am},\y{Am})/1cm)},
\n{a}={abs(\n{u}*(\n{Ap}+\n{Am})/2/(\n{u}+\n{v}+\n{w}))},
\n{b}={abs(\n{u}*(\n{Ap}-\n{Am})/2/(\n{u}+\n{v}+\n{w}))}
in [gset={a\X}{\n{a}},gset={b\X}{\n{b}},gset={phi\X}{\n{phi}}]
[rotate=\n{phi}] (M_\X)
circle[x radius=\n{a},y radius=\n{b}];
}
\draw[fill=orange!20,even odd rule] circle[x radius=a,y radius=b] foreach \X in {1,2,3}
{[rotate={gval("phi\X")}] (M_\X) circle[x radius={gval("a\X")},y radius={gval("b\X")}]};
\foreach \Y [count=\X] in {green,red,blue}
{\draw[fill/.expanded=\Y!20] {[rotate={gval("phi\X")}] (M_\X) circle[x radius={gval("a\X")},y radius={gval("b\X")}]};}
\tikzset{point on E/.style 2 args={insert path={[rotate={gval("phi#1")}] ($(M_#1)+({#2}:{{gval("a#1")} and {gval("b#1")}})$)}},
declare function={myslope(\x,\y)=Eslope(gval("a\x"),gval("b\x"),\y)+gval("phi\x");}}
\colorlet{c12}{blue}
\colorlet{c13}{red}
\colorlet{c23}{green!60!black}
\foreach \X/\Y/\Z/\myfirstA/\myfirstB
in {1/2/1/-110/40,1/2/2/-40/110,1/3/1/-120/-170,1/3/2/-40/30,2/3/1/-30/-20,2/3/2/-140/210}
{\path foreach \Iteration [remember=\myA as \myA (initially \myfirstA),remember=\myB as \myB (initially \myfirstB)] in {1,...,5}
{%\pgfextra{\typeout{myA=\myA, myB=\myB}}
{[point on E={\X}{\myA}] coordinate (p\X\Y-\Z-\X)} {[point on E={\Y}{\myB}] coordinate (p\X\Y-\Z-\Y)}
let \p1=($(p\X\Y-\Z-\X)-(p\X\Y-\Z-\Y)$),\n1={scalar(atan2(\y1,\x1))},
\n{A1}={MassageAngle(myslope("\X",\myA)-\n1)},\n{A2}={MassageAngle(myslope("\X",\myA)-\n1+180)},
\n{A}={(abs(\n{A1})<abs(\n{A2})?\n{A1}:\n{A2})},
\n{B1}={MassageAngle(myslope("\Y",\myB)-\n1)},\n{B2}={MassageAngle(myslope("\Y",\myB)-\n1+180)},
\n{B}={(abs(\n{B1})<abs(\n{B2})?\n{B1}:\n{B2})}
in \pgfextra{%\typeout{Delta A=\n{A}, Delta B=\n{B}}
\pgfmathsetmacro{\myA}{\myA-0.5*\n{A}}\pgfmathsetmacro{\myB}{\myB-0.5*\n{B}}}
}
(p\X\Y-\Z-\X) edge[shorten >=-2cm,shorten <=-2cm,color/.expanded=c\X\Y] (p\X\Y-\Z-\Y);}
\draw[shorten >=-1cm,shorten <=-1cm,magenta,semithick] foreach \X/\Y in {1/2,1/3,2/3}
{(intersection of p\X\Y-1-\X--p\X\Y-1-\Y\space and p\X\Y-2-\X--p\X\Y-2-\Y) coordinate[c] (i\X\Y-\X) }
(intersection of p12-1-1--p12-1-2 and p12-2-1--p12-2-2)
-- (intersection of p23-1-2--p23-1-3 and p23-2-2--p23-2-3);
\path foreach \X in {X,Y} {foreach \Y in {1,2,3} {(\X_\Y) node[c]{}}} ;
% \path foreach \X in {1,2,3} {{[point on E={\X}{0}] node{\X-0}} {[point on E={\X}{90}] node{\X-90}}};
\end{tikzpicture}
\end{document}
```
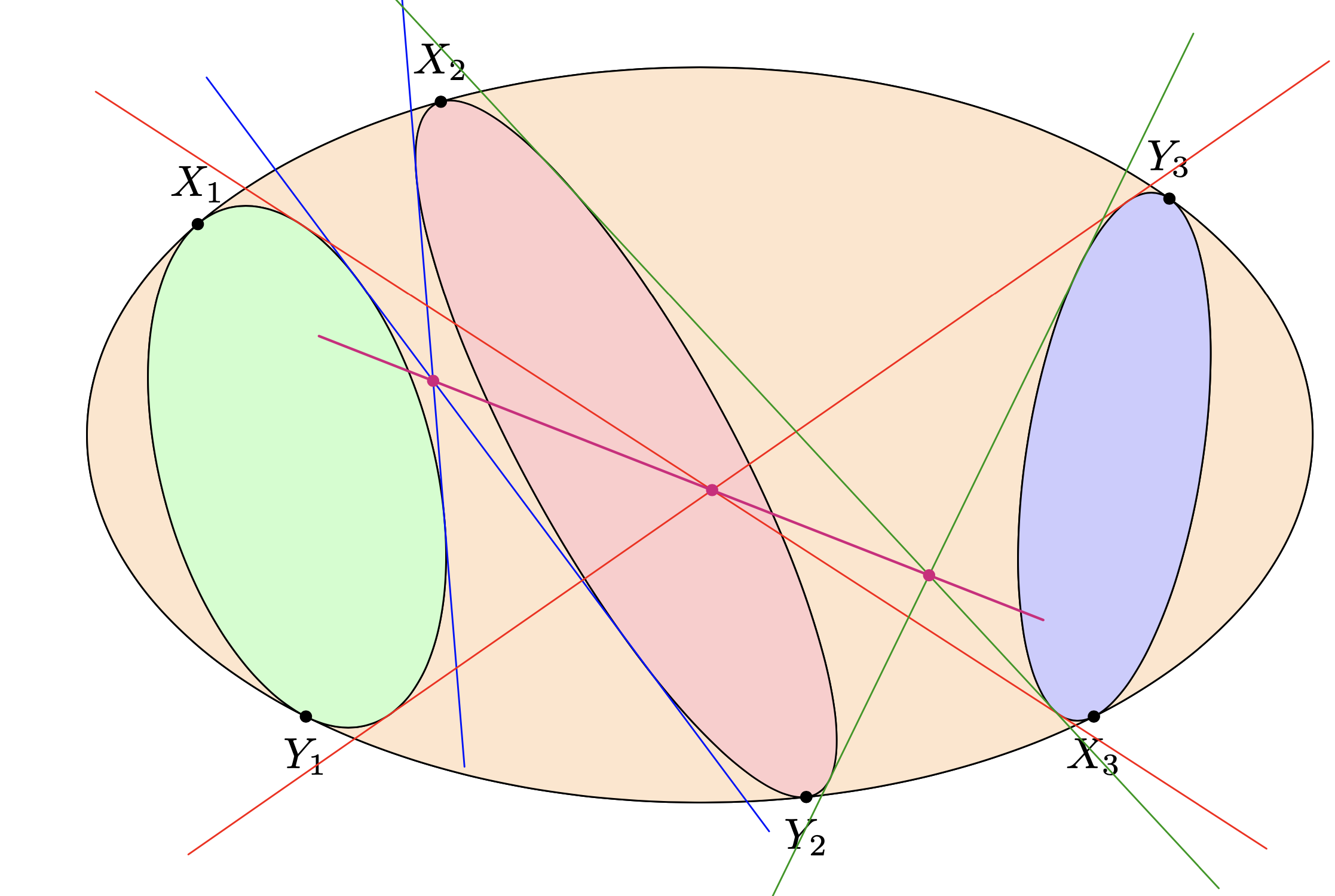
The construction follows [this article](https://forumgeom.fau.edu/FG2010volume10/FG201016.pdf), which describes how to inscribe an ellipse into a triangle in such a way that it touches the triangle in two predetermined points. (The construction uses the fact that triangle with an inscribed ellipse can be obtained from a projection of a triangle with an inscribed circle. Unfortunately I was unable to use this fact to define a simpler procedure that is doable with LaTeX, which is very painful when it comes to 3x3 matrix manipulations. I have no clue why, say, `E_1` appears on the last slide and not on the on slide 8. The code is also otherwise not polished, varous `_1` really should be `_\X` but in the above code this is fixed.)
```
\documentclass[fleqn]{beamer}
\usepackage{tikz}
\usetikzlibrary{calc,overlay-beamer-styles}%
\tikzset{V/.style args={<#1>#2}{alt=<#1>{opacity=1}{opacity=0},
label={[alt=<#1>{opacity=1}{opacity=0}]#2}}}
\begin{document}
\begin{frame}[t]
\frametitle{Inscribing ellipses with \LaTeX\ (cough)}
\begin{tikzpicture}[line join = round, line cap = round,>=stealth,
c/.style={circle,fill,inner sep=1pt},
declare function={a=2.8;b=1.5;
alpha1=145;beta1=230;
x1=0.4;y1=0.6;
eslope(\t)=atan2(b*cos(\t),-a*sin(\t));
baryn(\xA,\yA,\xB,\yB,\xC,\yC)=scalar((\xA/1cm-\xC/1cm)*(\yB/1cm-\yC/1cm)-(\xB/1cm-\xC/1cm)*(\yA/1cm-\yC/1cm));
baryu(\xB,\yB,\xC,\yC,\xP,\yP)=scalar((\yB/1cm-\yC/1cm)*(\xP/1cm-\xC/1cm)+(\xC/1cm-\xB/1cm)*(\yP/1cm-\yC/1cm));
baryv(\xA,\yA,\xC,\yC,\xP,\yP)=scalar((\yC/1cm-\yA/1cm)*(\xP/1cm-\xC/1cm)+(\xA/1cm-\xC/1cm)*(\yP/1cm-\yC/1cm));
barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryu(\xB,\yB,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryv(\xA,\yA,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda3(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(1-barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)-barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP));
}]
\path (-5,0);
\draw circle[x radius=a,y radius=b];
\path
foreach \X in {1}
{(alpha\X:a and b) coordinate[c,V=<2->{above:{$X_{\X}$}}] (X_\X)
++ ({scalar(eslope(alpha1))}:2) coordinate (aux1)
(beta\X:a and b) coordinate[c,V=<2->{below:{$Y_{\X}$}}] (Y_\X)
++ ({scalar(eslope(beta1))}:2) coordinate (aux2)
(X_\X) edge[visible on=<3>,->] (aux1)
(Y_\X) edge[visible on=<3>,->] (aux2)
(intersection of X_1--aux1 and Y_1--aux2)
coordinate[c,V=<3->{above:{$C_{\X}$}}] (C_\X)
($(X_\X)+x1*(X_\X)-x1*(C_1)$) coordinate[c,V=<4->{above:{$B_{\X}$}}] (B_\X)
($(Y_\X)+y1*(Y_\X)-y1*(C_1)$) coordinate[c,V=<4->{below:{$A_{\X}$}}] (A_\X)
(intersection of X_1--A_1 and Y_1--B_1)
coordinate[c,V=<5-6>{above:{$P_{\X}$}}] (P_\X)
};
\foreach \X in {1}
{\draw[visible on=<4->,blue,dashed] (A_\X.center) -- (B_\X.center) -- (C_\X.center) -- cycle;
\draw[overlay,visible on=<13->]
($0.333*(A_\X)+0.333*(B_\X)+0.333*(C_\X)$) coordinate (O_\X)
let \p{A}=($(A_\X)-(O_\X)$),\p{B}=($(B_\X)-(O_\X)$),\p{C}=($(C_\X)-(O_\X)$),\p{P}=($(P_\X)-(O_\X)$),
\n{A}={barylambda1(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{B}={barylambda2(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{C}={barylambda3(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{u}={\n{A}*(\n{B}+\n{C})},
\n{v}={\n{B}*(\n{C}+\n{A})},
\n{w}={\n{C}*(\n{A}+\n{B})}
in
(barycentric cs:A_\X=\n{u},B_\X=\n{v},C_\X=\n{w})
coordinate[c,V=<6->{below:{$M_\X$}}] (M_\X)
(intersection of B_\X--M_\X\space and A_\X--C_\X) coordinate[c,V=<7->{right:{$B_{0}$}}] (B_0)
(intersection of C_\X--M_\X\space and A_\X--B_\X) coordinate[c,V=<7->{right:{$C_{0}$}}] (C_0)
(B_\X) edge[visible on=<7>,dashed] (B_0)
(C_\X) edge[visible on=<7>,dashed] (C_0)
($(A_\X)+(B_0)-(B_\X)$) coordinate (auxAB)
($(A_\X)+(C_0)-(C_\X)$) coordinate (auxAC)
(intersection of A_\X--auxAB and B_\X--C_\X)
coordinate[c,V=<8->{right:{$D_\X$}}] (D_\X)
(intersection of A_\X--auxAC and B_\X--C_\X)
coordinate[c,V=<8->{right:{$E_\X$}}] (E_\X)
let
\p{BC}=($(C_\X)-(B_\X)$),\n{BC}={scalar(veclen(\x{BC},\y{BC})/1cm)},
\p{BD}=($(B_\X)-(D_\X)$),\n{BD}={scalar(veclen(\x{BD},\y{BD})/1cm)},
\p{CE}=($(C_\X)-(E_\X)$),\n{CE}={scalar(veclen(\x{CE},\y{CE})/1cm)},
\n{x}={(\n{BD}*\n{BD}-\n{CE}*\n{CE}+\n{BC}*\n{BC})/2/\n{BC}},
\n{y}={sqrt(\n{BD}*\n{BD}-\n{x}*\n{x})},
\n{phi}={scalar(atan2(\y{BC},\x{BC}))}
in ($(B_\X)+(\n{phi}:\n{x})+(\n{phi}+90:\n{y})$) coordinate (Ap)
($(B_\X)+(\n{phi}:\n{x})+(\n{phi}-90:\n{y})$) coordinate (Am)
let \p1=($(Ap)-(A_\X)$),\p2=($(Am)-(A_\X)$),
\n1={veclen(\x2,\y2)-veclen(\x1,\y1)} in
\ifdim\n1>0pt\relax
(Ap) coordinate[c,V=<10->{below:{$A_+$}}] (Ap)
(Am) coordinate[c,V=<10->{below:{$A_-$}}] (Am)
\else
(Am) coordinate[c,V=<10->{below:{$A_+$}}] (Ap)
(Ap) coordinate[c,V=<10->{below:{$A_-$}}] (Am)
\fi
let \p{p}=($(Ap)-(A_\X)$),\p{m}=($(Am)-(A_\X)$),
\n{bis}={scalar(0.5*atan2(\y{p},\x{p})+0.5*atan2(\y{m},\x{m}))}
in ($(A_\X)+(\n{bis}:2)$) coordinate (Abis)
(intersection of A_\X--Abis and B_\X--C_\X)
coordinate[c,V=<12->{below:{$Q_\X$}}] (Q_\X)
let \p{Q}=($(Q_\X)-(A_\X)$),
\n{phi}={scalar(atan2(\y{Q},\x{Q}))}
in (M_\X) edge[red,visible on=<12>] ++ (\n{phi}:2)
let \p{Ap}=($(Ap)-(A_\X)$),\p{Am}=($(Am)-(A_\X)$),
\n{Ap}={scalar(veclen(\x{Ap},\y{Ap})/1cm)},
\n{Am}={scalar(veclen(\x{Am},\y{Am})/1cm)},
\n{a}={\n{u}*(\n{Ap}+\n{Am})/2/(\n{u}+\n{v}+\n{w})},
\n{b}={\n{u}*(\n{Ap}-\n{Am})/2/(\n{u}+\n{v}+\n{w})}
in
[rotate=\n{phi}] (M_\X)
circle[x radius=\n{a},y radius=\n{b}];
\draw[visible on=<9-10>,dashed,overlay]
let \p1=($(B_\X)-(D_\X)$),\n1={veclen(\x1,\y1)} in
(B_\X) circle[radius=\n1];
\draw[visible on=<9-10>,dashed,overlay]
let \p1=($(C_\X)-(E_\X)$),\n1={veclen(\x1,\y1)} in
(C_\X) circle[radius=\n1];}
\end{tikzpicture}
\only<.(1)>{We are given an ellipse and want inscribe another ellipse. Let's
call the half-axes of the outer ellipse $a$ and $b$.}
\pause
\only<.(1)>{We call the touching points $X_1$ and $Y_1$. They can be
characterized by two ``angles'', $\alpha_1$ and $\beta_1$, i.e.
\[
X_1=\begin{pmatrix} a\,\cos\alpha_1\\ b\,\sin\alpha_1\end{pmatrix}
\quad\text{and}\quad
Y_1=\begin{pmatrix} a\,\cos\beta_1\\ b\,\sin\beta_1\end{pmatrix}\;.
\]
These two points do not specify the inscribed ellipse uniquely. We
need another constraint.}
\pause
\only<.(1)>{We know the slopes at $X_1$ and $Y_1$,
\[
\dot X_1=\begin{pmatrix} -a\,\sin\alpha_1\\ b\,\cos\alpha_1\end{pmatrix}
\quad\text{and}\quad
\dot Y_1=\begin{pmatrix} -a\,\sin\beta_1\\ b\,\cos\beta_1\end{pmatrix}\;.
\]
Call the point at which the tangents intersect $C_1$.}
\pause
\only<.(1)>{The lines $C_1X_1$ and $C_1Y_1$ can be extended to some points
$B_1$ and $A_1$, respectively. Then the requirement that the ellipse be
inscribed in the triangle $A_1B_1C_1$ fixes the ellipse uniquely.}
\pause
\only<.(1)>{We also have enough information to construct the so-called
perspector, $P_1$, and to exploit the results from a nice
\href{https://forumgeom.fau.edu/FG2010volume10/FG201016.pdf}{article by
Nikolaos Dergiades} on the geometry forum.}
\pause
\only<.(1)>{In particular, the \href{https://forumgeom.fau.edu/FG2010volume10/FG201016.pdf}{article}
describes how barycentric coordinates allow us to find the center, $M_1$, of the
ellipse.
\href{https://en.wikipedia.org/wiki/Barycentric_coordinate_system}{Translating
Cartesian coordinates to barycentric ones} is something that still can be done
with \LaTeX, but it's starting to become cumbersome.}
\pause
\only<.(1)>{We can then determine the cevian points $B_0$ and $C_0$ from
intersections.}
\pause
\only<.(1)>{The parallels of $B_1B_0$ and $C_1C_0$ through $A_1$ to
intersect $B_1C_1$ at $D_1$ and $E_1$ respectively.}
\pause
\only<.(1)>{Next construct circles with centers $B_1$ and $C_1$ going through
$D_1$ and $E_1$, respectively.}
\pause
\only<.(1)>{Construct the intersections of these two circles,
$A_+$ and $A_-$. $A_+$ is the intersections which is closer to $A_1$.}
\pause
\only<.(1)>{The half-axes of the ellipse are given by
\begin{align*}
a_1&=\frac{u(|A_1A_+|+|A_1A_-|)}{2(u+v+w)}\;,\\
b_1&=\frac{u(|A_1A_+|-|A_1A_-|)}{2(u+v+w)}\;.
\end{align*}}
\pause
\only<.(1)>{The internal bisector of $A_+A_1A_-$ intersects with $B_1C_1$
at $Q_1$. $A_1Q_1$ is the direction of the longer axis.}
\pause
\only<.(1)>{This gives us enough milage to draw the ellipse.}
\end{frame}
\end{document}
```

This can be used to draw three ellipses, of course. (I seem to make a discrete choice somewhere, so the `X_i` want to sit in the top left or bottom right quadrants, i.e. `xi` should be between 90 and 180 or 270 and 360. That is, for certain angles you need to swap the roles of `X_i` and `Y_i` to get the desired ellipse.)
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}%
\begin{document}
\begin{tikzpicture}[line join = round, line cap = round,>=stealth,
c/.style={circle,fill,inner sep=1pt},
declare function={a=5;b=3;
alpha1=145;beta1=230;x1=0.4;y1=0.6;
alpha2=115;beta2=280;x2=0.02;y2=0.03;
alpha3=310;beta3=40;x3=0.2;y3=0.3;
eslope(\t)=atan2(b*cos(\t),-a*sin(\t));
baryn(\xA,\yA,\xB,\yB,\xC,\yC)=scalar((\xA/1cm-\xC/1cm)*(\yB/1cm-\yC/1cm)-(\xB/1cm-\xC/1cm)*(\yA/1cm-\yC/1cm));
baryu(\xB,\yB,\xC,\yC,\xP,\yP)=scalar((\yB/1cm-\yC/1cm)*(\xP/1cm-\xC/1cm)+(\xC/1cm-\xB/1cm)*(\yP/1cm-\yC/1cm));
baryv(\xA,\yA,\xC,\yC,\xP,\yP)=scalar((\yC/1cm-\yA/1cm)*(\xP/1cm-\xC/1cm)+(\xA/1cm-\xC/1cm)*(\yP/1cm-\yC/1cm));
barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryu(\xB,\yB,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(baryv(\xA,\yA,\xC,\yC,\xP,\yP)/baryn(\xA,\yA,\xB,\yB,\xC,\yC));
barylambda3(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)=scalar(1-barylambda1(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP)-barylambda2(\xA,\yA,\xB,\yB,\xC,\yC,\xP,\yP));
}]
\draw circle[x radius=a,y radius=b];
\foreach \X in {1,2,3}
{\path
(alpha\X:a and b) coordinate (aux) let \p1=(aux) in
\ifdim\y1>0pt\relax
coordinate[c,label={above:{$X_{\X}$}}] (X_\X)
\else
coordinate[c,label={below:{$X_{\X}$}}] (X_\X)
\fi
++ ({scalar(eslope(alpha\X))}:2) coordinate (aux1)
(beta\X:a and b) coordinate (aux) let \p1=(aux) in
\ifdim\y1>0pt\relax
coordinate[c,label={above:{$Y_{\X}$}}] (Y_\X)
\else
coordinate[c,label={below:{$Y_{\X}$}}] (Y_\X)
\fi
++ ({scalar(eslope(beta\X))}:2) coordinate (aux2);
\draw[overlay]
(intersection of X_\X--aux1 and Y_\X--aux2)
coordinate (C_\X)
($(X_\X)+x\X*(X_\X)-x\X*(C_\X)$) coordinate (B_\X)
($(Y_\X)+y\X*(Y_\X)-y\X*(C_\X)$) coordinate (A_\X)
(intersection of X_\X--A_\X\space and Y_\X--B_\X)
coordinate (P_\X)
($0.333*(A_\X)+0.333*(B_\X)+0.333*(C_\X)$) coordinate (O_\X)
let \p{A}=($(A_\X)-(O_\X)$),\p{B}=($(B_\X)-(O_\X)$),\p{C}=($(C_\X)-(O_\X)$),\p{P}=($(P_\X)-(O_\X)$),
\n{A}={barylambda1(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{B}={barylambda2(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{C}={barylambda3(\x{A},\y{A},\x{B},\y{B},\x{C},\y{C},\x{P},\y{P})},
\n{u}={\n{A}*(\n{B}+\n{C})},
\n{v}={\n{B}*(\n{C}+\n{A})},
\n{w}={\n{C}*(\n{A}+\n{B})}
in
(barycentric cs:A_\X=\n{u},B_\X=\n{v},C_\X=\n{w})
coordinate (M_\X)
(intersection of B_\X--M_\X\space and A_\X--C_\X) coordinate (B_0)
(intersection of C_\X--M_\X\space and A_\X--B_\X) coordinate (C_0)
($(A_\X)+(B_0)-(B_\X)$) coordinate (auxAB)
($(A_\X)+(C_0)-(C_\X)$) coordinate (auxAC)
(intersection of A_\X--auxAB and B_\X--C_\X)
coordinate (D_\X)
(intersection of A_\X--auxAC and B_\X--C_\X)
coordinate (E_\X)
let
\p{BC}=($(C_\X)-(B_\X)$),\n{BC}={scalar(veclen(\x{BC},\y{BC})/1cm)},
\p{BD}=($(B_\X)-(D_\X)$),\n{BD}={scalar(veclen(\x{BD},\y{BD})/1cm)},
\p{CE}=($(C_\X)-(E_\X)$),\n{CE}={scalar(veclen(\x{CE},\y{CE})/1cm)},
\n{x}={(\n{BD}*\n{BD}-\n{CE}*\n{CE}+\n{BC}*\n{BC})/2/\n{BC}},
\n{y}={sqrt(\n{BD}*\n{BD}-\n{x}*\n{x})},
\n{phi}={scalar(atan2(\y{BC},\x{BC}))}
in ($(B_\X)+(\n{phi}:\n{x})+(\n{phi}+90:\n{y})$) coordinate (Ap)
($(B_\X)+(\n{phi}:\n{x})+(\n{phi}-90:\n{y})$) coordinate (Am)
let \p1=($(Ap)-(A_\X)$),\p2=($(Am)-(A_\X)$),
\n1={veclen(\x2,\y2)-veclen(\x1,\y1)} in
\ifdim\n1>0pt\relax
(Ap) coordinate (Ap)
(Am) coordinate (Am)
\else
(Am) coordinate (Ap)
(Ap) coordinate (Am)
\fi
let \p{p}=($(Ap)-(A_\X)$),\p{m}=($(Am)-(A_\X)$),
\n{bis}={scalar(0.5*atan2(\y{p},\x{p})+0.5*atan2(\y{m},\x{m}))}
in ($(A_\X)+(\n{bis}:2)$) coordinate (Abis)
(intersection of A_\X--Abis and B_\X--C_\X)
coordinate (Q_\X)
let \p{Q}=($(Q_\X)-(A_\X)$),
\n{phi}={scalar(atan2(\y{Q},\x{Q}))}
in
let \p{Ap}=($(Ap)-(A_\X)$),\p{Am}=($(Am)-(A_\X)$),
\n{Ap}={scalar(veclen(\x{Ap},\y{Ap})/1cm)},
\n{Am}={scalar(veclen(\x{Am},\y{Am})/1cm)},
\n{a}={\n{u}*(\n{Ap}+\n{Am})/2/(\n{u}+\n{v}+\n{w})},
\n{b}={\n{u}*(\n{Ap}-\n{Am})/2/(\n{u}+\n{v}+\n{w})}
in
[rotate=\n{phi}] (M_\X)
circle[x radius=\n{a},y radius=\n{b}];
}
\end{tikzpicture}
\end{document}
```