I use `3dtools` to draw a cube. I tried
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},line cap=butt,line join=round,c/.style={circle,fill,inner sep=1pt},
declare function={a=3;}]
\path
(a,-a,-a) coordinate (A)
(a,a,-a) coordinate (B)
(-a,a,-a) coordinate (C)
(-a,-a,-a) coordinate (D)
(a,-a,a) coordinate (E)
(a,a,a) coordinate (F)
(-a,a,a) coordinate (G)
(-a,-a,a) coordinate (H)
(0,0,0) coordinate (O)
;
\tikzset{3d/polyhedron/.cd,O={(O)},
back/.style={3d/polyhedron/complete dashes,fill=none},
fore/.style={3d/visible,fill=none},draw face with corners={{(B)},{(C)},{(G)},{(F)}},
draw face with corners={{(D)},{(C)},{(G)},{(H)}},
draw face with corners={{(E)},{(F)},{(G)},{(H)}},
draw face with corners={{(A)},{(B)},{(C)},{(D)}},
draw face with corners={{(A)},{(B)},{(F)},{(E)}},
draw face with corners={{(A)},{(E)},{(H)},{(D)}}
}
%\path foreach \p/\g in {A/-90,B/90,C/0,D/0,E/0,F/0,G/0,H/0}{(\p)node[c]{}+(\g:2.5mm) node{$\p$}};
\end{tikzpicture}
\end{document}
```
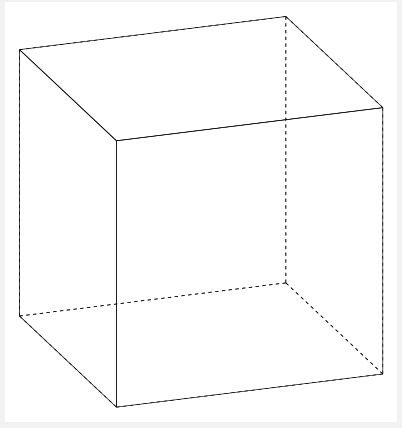
From the internet, I see this picture
Is this an orthonormal projection of a cube? What is a nice way to draw a cube?
The projection you depict is not orthographic, and hence cannot be obtained with `3d/install view`. I recycle the proof of the first statement from [here](https://tex.stackexchange.com/a/448048). You can still use `3dtools` to draw the cube, but this amounts to either being lucky of defining your own function for the screen depth. In this case we are lucky, but I show nevertheless how to override the `screendepth` function.
```
\documentclass[fleqn]{article}
\usepackage{amsmath}
\usepackage{marvosym}
\usepackage{tikz}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
You wish to have a coordinate system that
\begin{enumerate}
\item preserves shapes and\label{preserve}
\item has $\vec e_y$ point east, $\vec e_z$ point north and $\vec e_x$ point
south west.\label{directions}
\end{enumerate}
The first requirement means that the coordinate axes are orthogonal,
\begin{equation}\label{eq:orthogonality}
\vec e_x\cdot \vec e_y=\vec e_x\cdot \vec e_z=\vec e_y\cdot \vec e_z
=0\;.
\end{equation}
So we wish to find a two--dimensional projection of these vectors that fulfill
the requirement \ref{directions}. Decompose the vectors in two--dimensional
projections on the paper plane $\vec e_i^{(\|)}$ and the orthogonal complements
$\vec e_i^{(\perp)}$. Clearly, the $\vec e_i^{(\perp)}$ are just
one--dimensional objects, which we will just call $e_i^{(\perp)}$. Requirement \ref{directions} implies that
\begin{equation}
\vec e_x^{(\|)} \cdot \vec e_y^{(\|)}=
\vec e_x^{(\|)} \cdot \vec e_z^{(\|)}=:\xi\ne0\;.
\end{equation}
Due to the orthogonality relations \eqref{eq:orthogonality}, this means that
\begin{equation}
e_x^{(\perp)} \cdot e_y^{(\perp)}=
e_x^{(\perp)} \cdot e_z^{(\perp)}=-\xi\ne0\;.
\end{equation}
None of the $e_i^{(\perp)}$ may vanish as otherwise there won't be an $x$--axis,
and
\begin{equation}
e_y^{(\perp)}=e_z^{(\perp)}=-\frac{\xi}{e_x^{(\perp)}}\;.
\end{equation}
However, requirement \ref{directions}
implies that $\vec e_y^{(\|)} \cdot \vec e_z^{(\|)}=0$, so
\begin{equation}
\vec e_y\cdot \vec e_z=\vec e_y^{(\|)} \cdot \vec e_z^{(\|)}
+e_y^{(\perp)} \cdot e_z^{(\perp)}=0+\left(\frac{\xi}{e_x^{(\perp)}}\right)^2
\ne0\;.\qquad \text{\Huge\Lightning}
\end{equation}
%\clearpage
Having seen that the desired projection is not orthonormal, one may ask whether
it is possible to use \texttt{3dtools} for such projections. The answer is that
this is in principle possible. You can define your own \texttt{screendepth}
function, in this very case this is not even necessary. However, in general it
won't be easy to guess an appropriate fuction.
\begin{figure}[htb]
\centering
\begin{tikzpicture}
\pgfmathdeclarefunction*{screendepth}{3}{\pgfmathparse{0.2*#1+0.2*#2+#3}}
\path foreach \Xa/\Ya in {-1/A,1/B}
{foreach \Xb/\Yb in {-1/A,1/B}
{foreach \Xc/\Yc in {-1/A,1/B}
{(\Xa,\Xb,\Xc) coordinate (\Ya\Yb\Yc)}}} ;
\tikzset{3d/polyhedron/.cd,
fore/.append style={fill opacity=0.5},
edges have complete dashes,
draw face with corners={{(AAA)},{(AAB)},{(ABB)},{(ABA)}},
draw face with corners={{(AAA)},{(AAB)},{(BAB)},{(BAA)}},
draw face with corners={{(AAA)},{(BAA)},{(BBA)},{(ABA)}},
draw face with corners={{(BAA)},{(BAB)},{(BBB)},{(BBA)}},
draw face with corners={{(ABA)},{(ABB)},{(BBB)},{(BBA)}},
draw face with corners={{(AAB)},{(BAB)},{(BBB)},{(ABB)}}}
\end{tikzpicture}
\end{figure}
\end{document}
```

However, when using this projection, then it is no longer clear how to rotate the cube, etc. This projection can still be useful for sketches.