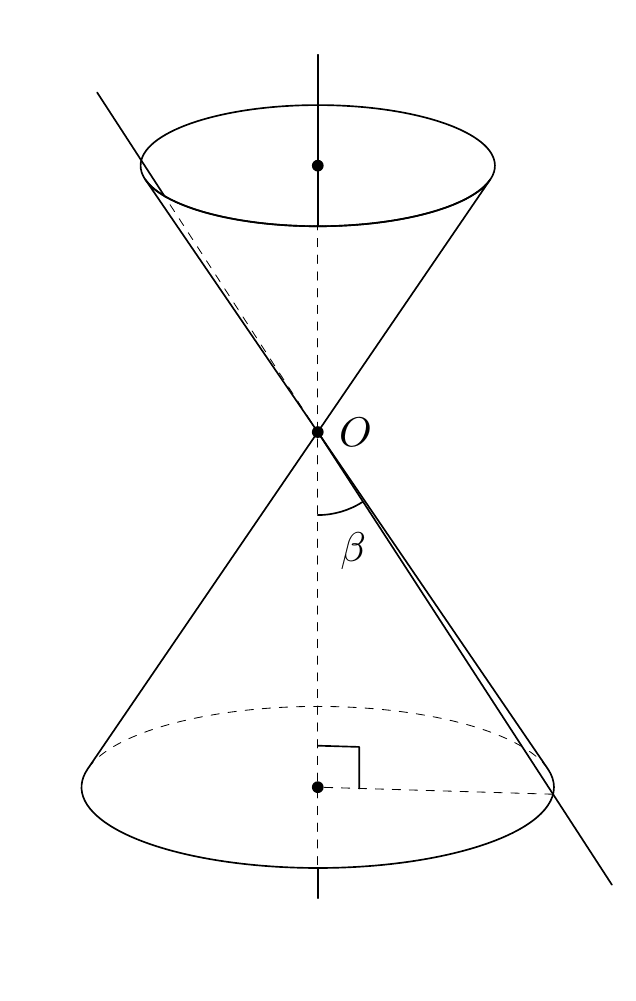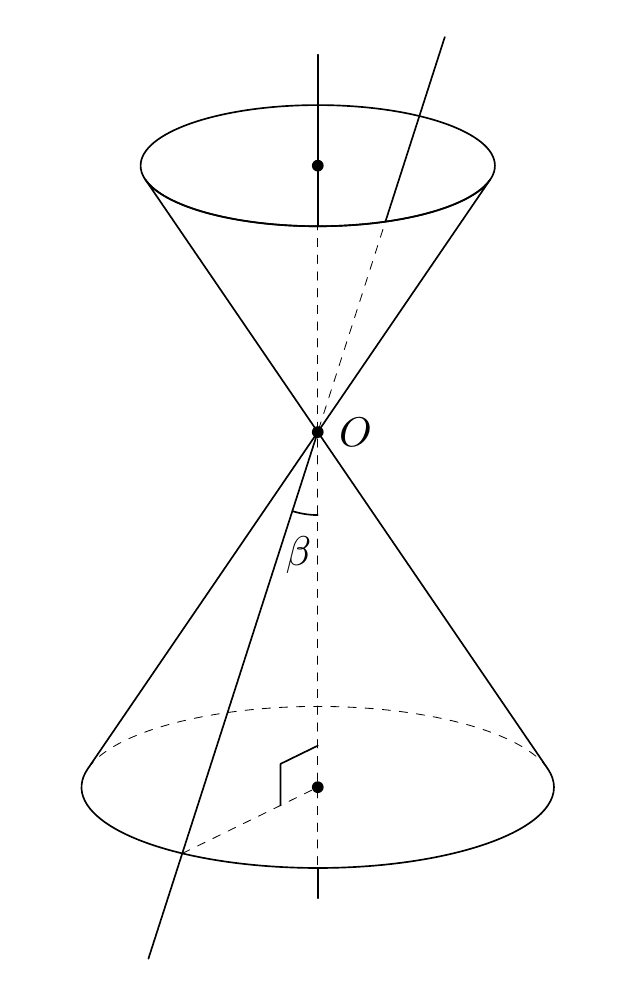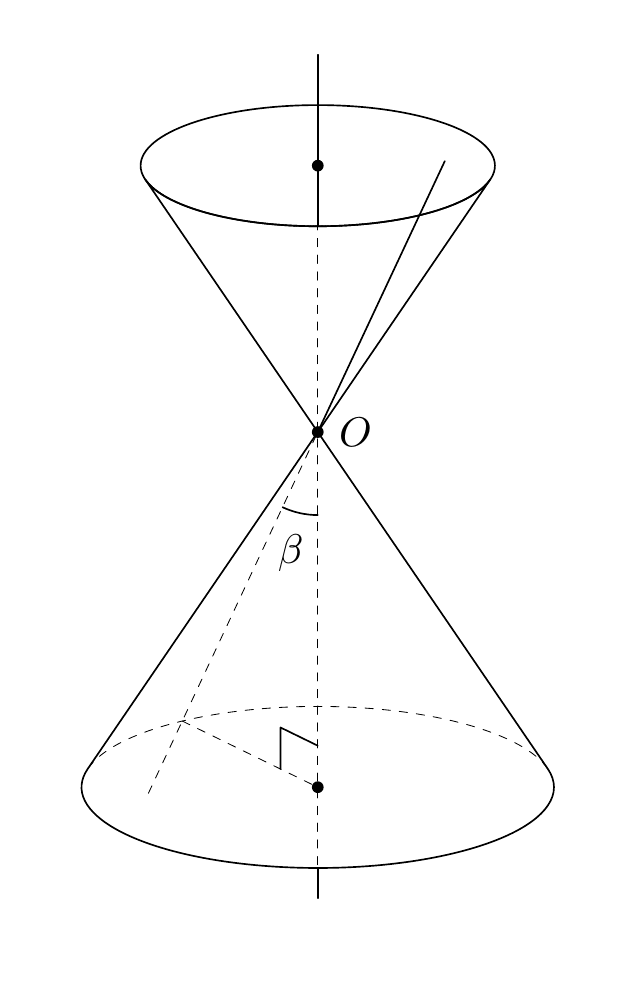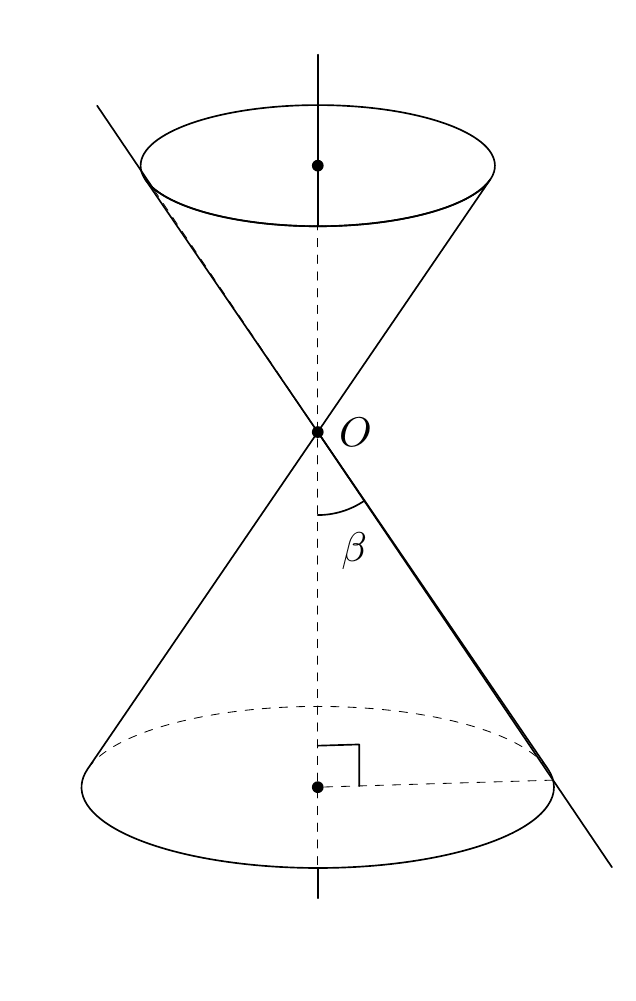
You can use the `3dtools` library, which you need to download separately from [its GitHub site](https://github.com/marmotghost/tikz-3dtools). It has a couple of features which can make it easier to distinguish between visible and hidden stretches, and comes with a number of predefined pics such as cones. So, for a fixed view one might simply do
```
\documentclass[border=2mm,tikz]{standalone}
\usetikzlibrary{angles,calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,
dot/.style={circle,fill,inner sep=1pt}]
\begin{scope}[3d/install view={phi=30,theta=70}]
\path (0,0,0) coordinate[dot,label=right:{$O$}] (O)
(2,0,-3.2) coordinate (A) (0,0,-3.2) coordinate[dot] (B)
pic[3d/cone/outer/.append style={save named path=lc}]{3d/cone={r=2,h=3.2}}
(0,0,2.4) coordinate[dot] (C)
pic[3d/cone/outer/.append style={save named path=uc}]{3d/cone={r=1.5,h=-2.4}};
\path[save named path=line] (2.5,0,-4) -- (-2,0,3.2);
\path[save named path=v] (0,0,-5) -- (0,0,4);
\tikzset{3d/ordered paths/.cd,lc/.style={draw=none},uc/.style={draw=none}}
\tikzset{3d/draw ordered paths={v,lc,line,uc}}
\begin{scope}[canvas is xz plane at y=0]
\draw[3d/hidden] (B) -- (A);
\pic[draw,pic text={$\beta$},angle radius=2em,angle eccentricity=1.5]{angle=B--O--A};
\pic[draw,angle radius=1em]{right angle=A--B--O};
\end{scope}
\end{scope}
\end{tikzpicture}
\end{document}
```
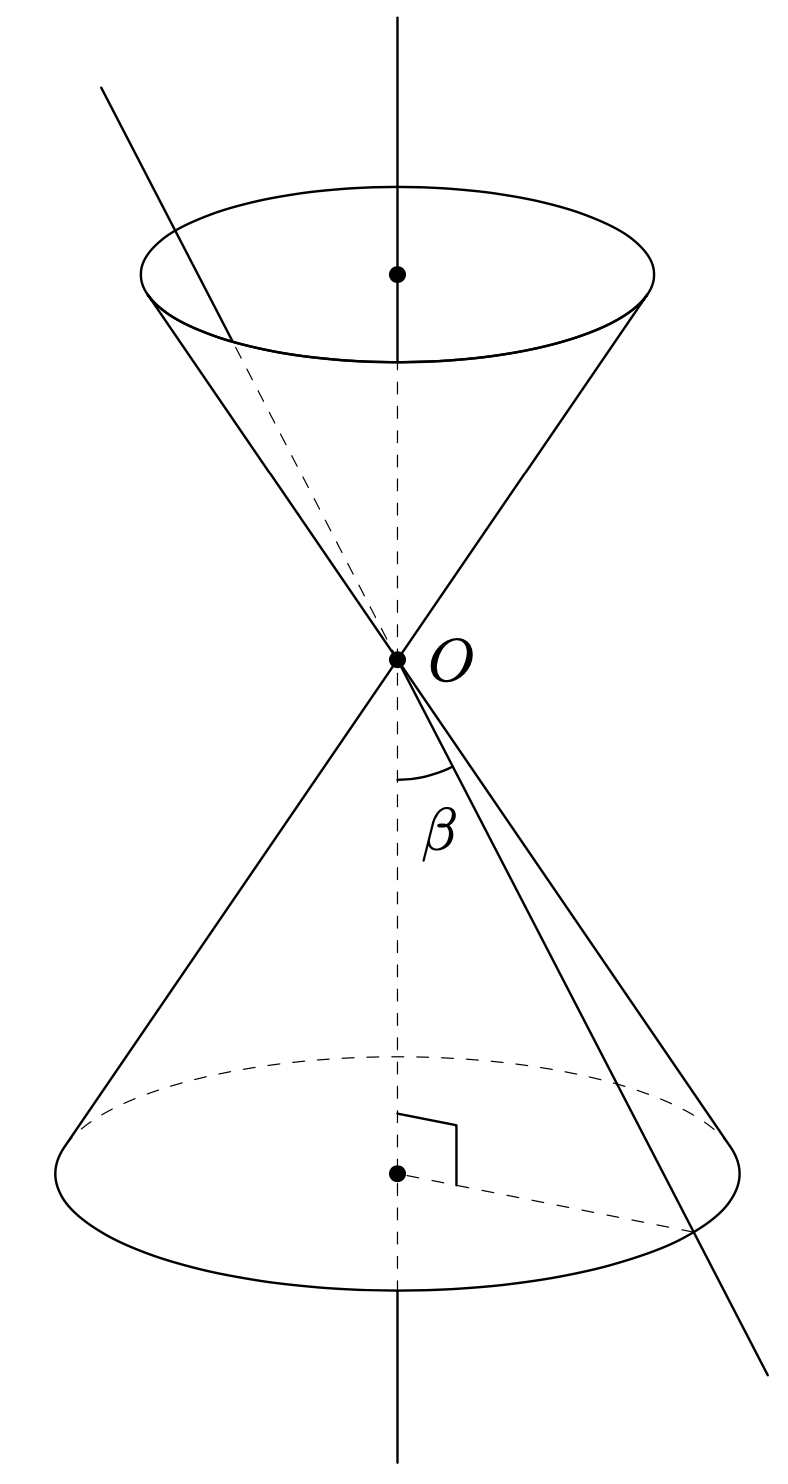
You can define the height of the lower cone `H`, the radius of its base `R`, and the height of the upper cone. This fixes the radius of the upper cone.
```
\documentclass[border=2mm,tikz]{standalone}
\usetikzlibrary{angles,calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,
dot/.style={circle,fill,inner sep=1pt},
declare function={R=2;H=3.2;r=1.5;}]
\begin{scope}[3d/install view={phi=30,theta=70}]
\path (0,0,0) coordinate[dot,label=right:{$O$}] (O)
(2,0,-H) coordinate (A) (0,0,-H) coordinate[dot] (B)
pic[3d/cone/outer/.append style={save named path=lc}]{3d/cone={r=R,h=H}}
(0,0,H*r/R) coordinate[dot] (C)
pic[3d/cone/outer/.append style={save named
path=uc}]{3d/cone={r=r,h/.evaluated=-H*r/R}};
\path[save named path=line] (1.25*R,0,-1.25*H) -- (-1.25*r,0,1.25*H*r/R);
\path[save named path=v] (0,0,-H-1) -- (0,0,H*r/R+1);
\pgfmathsetmacro{\mytheta}{asin(-1*y2d("B")/H/1cm)}
\pgfmathsetmacro{\myalpha}{asin(H*cot(\mytheta)/R)}
\pgfmathsetmacro{\myX}{TDunit("(0,0,1)x(nscreenx,nscreeny,nscreenz)")}
\pgfmathsetmacro{\myphi}{atan2({\myX}[0],{\myX}[1])}
\pgfmathsetmacro{\mysdcrit}{screendepth({R*cos(\myphi+\myalpha)},{R*sin(\myphi+\myalpha)},-H)}
\pgfmathtruncatemacro{\itest}{screendepth(2.5,0,-4)>\mysdcrit?1:0}
\tikzset{3d/ordered paths/.cd,lc/.style={draw=none},uc/.style={draw=none}}
\ifnum\itest=0
\tikzset{3d/draw ordered paths={v,uc,line,lc}}
\else
\tikzset{3d/draw ordered paths={v,lc,line,uc}}
\fi
\begin{scope}[canvas is xz plane at y=0]
\draw[3d/hidden] (B) -- (A);
\pic[draw,pic text={$\beta$},angle radius=2em,angle eccentricity=1.5]{angle=B--O--A};
\pic[draw,angle radius=1em]{right angle=A--B--O};
\end{scope}
\end{scope}
\end{tikzpicture}
\end{document}
```
This code is also "rotatable".
```
\documentclass[border=2mm,tikz]{standalone}
\usetikzlibrary{angles,calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\foreach \Angle in {5,15,...,355}
{\begin{tikzpicture}[line cap=round,line join=round,same bounding box=A,
dot/.style={circle,fill,inner sep=1pt},
declare function={R=2;H=3.2;r=1.5;}]
\begin{scope}[3d/install view={phi=\Angle,theta=70}]
\path (0,0,0) coordinate[dot,label=right:{$O$}] (O)
(2,0,-H) coordinate (A) (0,0,-H) coordinate[dot] (B)
pic[3d/cone/outer/.append style={save named path=lc}]{3d/cone={r=R,h=H}}
(0,0,H*r/R) coordinate[dot] (C)
pic[3d/cone/outer/.append style={save named
path=uc}]{3d/cone={r=r,h/.evaluated=-H*r/R}};
\path[save named path=line] (1.25*R,0,-1.25*H) -- (-1.25*r,0,1.25*H*r/R);
\path[save named path=v] (0,0,-H-1) -- (0,0,H*r/R+1);
\pgfmathsetmacro{\mytheta}{asin(-1*y2d("B")/H/1cm)}
\pgfmathsetmacro{\myalpha}{asin(H*cot(\mytheta)/R)}
\pgfmathsetmacro{\myX}{TDunit("(0,0,1)x(nscreenx,nscreeny,nscreenz)")}
\pgfmathsetmacro{\myphi}{atan2({\myX}[0],{\myX}[1])}
\pgfmathsetmacro{\mysdcrit}{screendepth({R*cos(\myphi+\myalpha)},{R*sin(\myphi+\myalpha)},-H)}
\pgfmathtruncatemacro{\itest}{screendepth(2.5,0,-4)>\mysdcrit?1:0}
\tikzset{3d/ordered paths/.cd,lc/.style={draw=none},uc/.style={draw=none}}
\ifnum\itest=0
\tikzset{3d/draw ordered paths={v,uc,line,lc}}
\else
\tikzset{3d/draw ordered paths={v,lc,line,uc}}
\fi
\begin{scope}[canvas is xz plane at y=0]
\draw[3d/hidden] (B) -- (A);
\pgfmathtruncatemacro{\jtest}{sin(\myphi)>0?1:0}
\ifnum\jtest=0
\pic[draw,pic text={$\beta$},angle radius=2em,angle eccentricity=1.5]{angle=A--O--B};
\else
\pic[draw,pic text={$\beta$},angle radius=2em,angle eccentricity=1.5]{angle=B--O--A};
\fi
\pic[draw,angle radius=1em]{right angle=A--B--O};
\end{scope}
\end{scope}
\end{tikzpicture}}
\end{document}
```