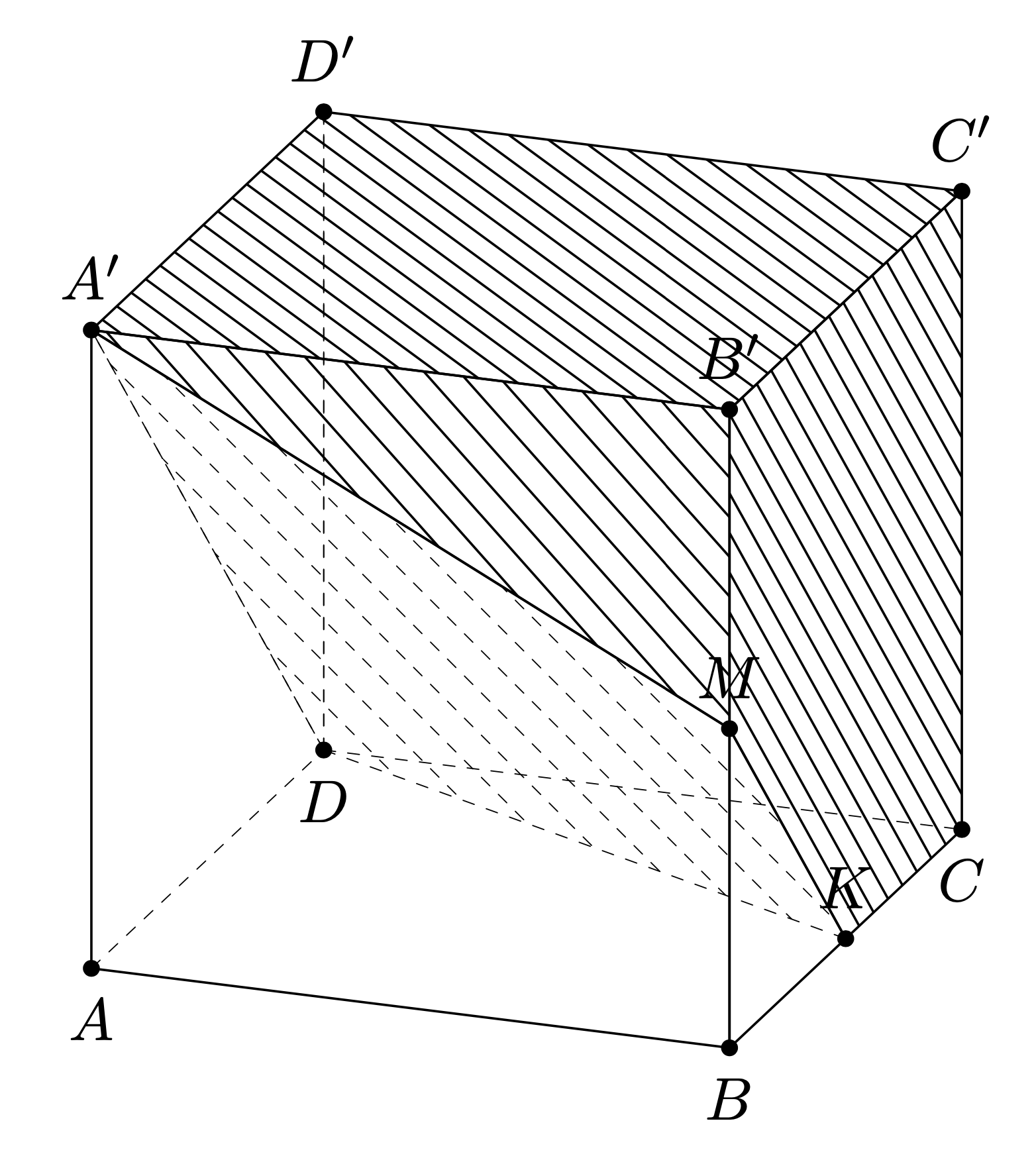
If you do not insist on transformed patterns, then everything is already part to the `3dtools` library. You just change the `fore` style for some of the faces.
```
\documentclass[tikz,border=3.14mm]{standalone}
\usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[3d/install view={phi=20,theta=70},line join = round,
line cap = round, declare function={a =2;},same bounding box=A,
c/.style={circle,fill,inner sep=1pt}]
\path
(-a,-a,-a) coordinate (A)
(a,-a,-a) coordinate (B)
(a,a,-a) coordinate (C)
(-a,a,-a) coordinate (D)
(-a,-a,a) coordinate (A')
(a,-a,a) coordinate (B')
(a,a,a) coordinate (C')
(-a,a,a) coordinate (D')
(a,0,-a) coordinate (K)
(a,-a,0) coordinate (M);
\tikzset{fore'/.style={fill opacity=0.5,draw,solid},
3d/polyhedron/.cd,O={(0,0,0)},fore/.style={fore',fill=none},
back/.append style={3d/hidden},
draw face with corners={{(B)},{(K)},{(M)}},
draw face with corners={{(A)},{(B)},{(M)},{(A')}},
draw face with corners={{(A)},{(D)},{(A')}},
draw face with corners={{(D)},{(D')},{(A')}},
draw face with corners={{(D)},{(D')},{(C')},{(C)}},
fore/.style={fore',fill=gray!50},
draw face with corners={{(A')},{(M)},{(B')}},
draw face with corners={{(A')},{(B')},{(C')},{(D')}},
draw face with corners={{(K)},{(C)},{(C')},{(B')},{(M)},{(K)}},
fore/.style={fore',draw=none,fill=blue!50},
draw face with corners={{(A')},{(D)},{(K)},{(M)}}
}
\draw[3d/hidden] (D) -- (K);
\path foreach \X in {A,...,D} {(\X) node[c,label={below:$\X$}]{}
(\X') node[c,label={above:$\X'$}]{}}
foreach \X in {K,M} {(\X) node[c,label={above:$\X$}]{}};
\end{tikzpicture}
\end{document}
```
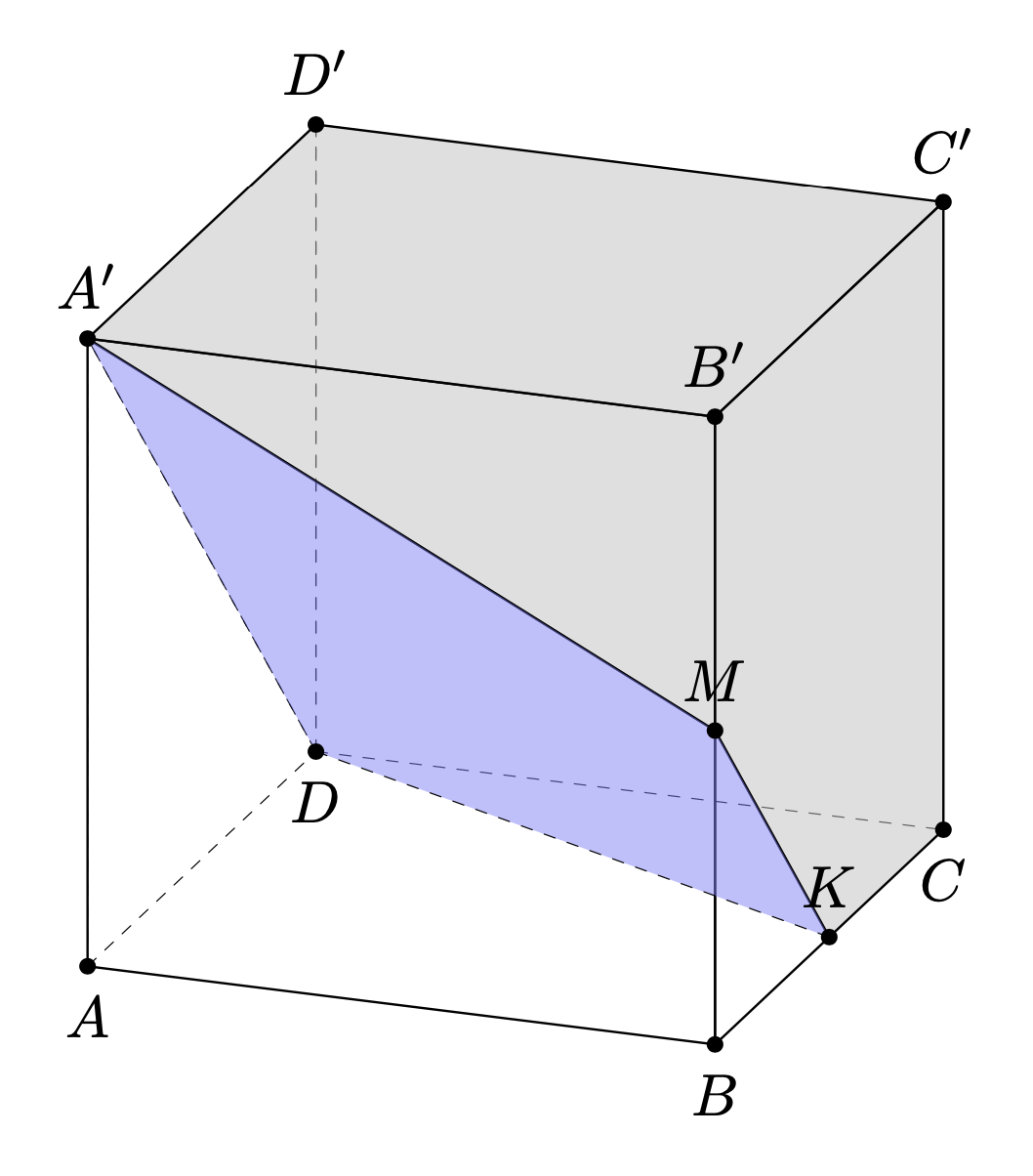
Obviously you can also use patterns from `patterns.meta`, say, to shade the faces. What won't happen there is that the patterns get transformed to the plane. In fact, even though it is straightforward to project pretty much anything on a plane, this is not the case for patterns, which are some low-level directives that directly talk to the driver (which is why, among other things, they may look different on a pdf and a pdf that has been converted to a bitmap, say). You can define (computationally expensive) pattern-like styles and project those. I copied a style from [this post](https://tex.stackexchange.com/a/593549) and slightly modified it to provide you with an explicit example. This pattern gets projected "obvious" planes like the `xy plane` from the `3d` library but also on a slightly less obvious one.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools
\tikzset{manual pattern/.style={manual pattern keys/.cd,#1,
/tikz/path picture={
\pgfmathsetmacro{\mybeta}{Mod(270+\pgfkeysvalueof{/tikz/manual pattern keys/angle},180)-90}
\pgfmathtruncatemacro{\myt}{\mybeta<-45?0:(\mybeta<0?1:(\mybeta<45?2:3))}
\def\myxshift{0pt}
\def\myyshift{0pt}
\ifcase\myt
\pgfmathsetmacro{\mydelta}{abs(cos(\mybeta))}
\pgfmathsetmacro{\myd}{1/abs(sin(\mybeta))}
\def\mystart{path picture bounding box.north west}
\def\myxshift{-\y1*\mydelta+\z*\pgfkeysvalueof{/tikz/manual pattern keys/distance}*\myd}
\or
\pgfmathsetmacro{\mydelta}{abs(sin(\mybeta))}
\pgfmathsetmacro{\myd}{1/abs(cos(\mybeta))}
\def\mystart{path picture bounding box.north west}
\def\myyshift{\x1*\mydelta-\z*\pgfkeysvalueof{/tikz/manual pattern keys/distance}*\myd}
\or
\pgfmathsetmacro{\mydelta}{abs(sin(\mybeta))}
\pgfmathsetmacro{\myd}{1/abs(cos(\mybeta))}
\def\mystart{path picture bounding box.south west}
\def\myyshift{-\x1*\mydelta+\z*\pgfkeysvalueof{/tikz/manual pattern keys/distance}*\myd}
\or
\pgfmathsetmacro{\mydelta}{abs(cos(\mybeta))}
\pgfmathsetmacro{\myd}{1/abs(sin(\mybeta))}
\def\mystart{path picture bounding box.south west}
\def\myxshift{-\y1*\mydelta+\z*\pgfkeysvalueof{/tikz/manual pattern keys/distance}*\myd}
\fi
\path
let \p1=($(path picture bounding box.north east)-(path picture bounding box.south west)$),
\n1={scalar(int(1+2*(\x1+\y1)/\pgfkeysvalueof{/tikz/manual pattern keys/distance}))},
\n2={max(\x1,\y1)*sqrt(2)}
in foreach \z in {-\n1,...,\n1}
{([xshift=\myxshift,yshift=\myyshift]\mystart)
edge[/tikz/manual pattern keys/lines] ++ (\mybeta:\n2)
};
}},manual pattern keys/.cd,distance/.initial=5pt,angle/.initial=-45,
lines/.style={draw}}
\begin{document}
\begin{tikzpicture}[3d/install view={phi=20,theta=70},line join = round,
line cap = round, declare function={a =2;},
c/.style={circle,fill,inner sep=1pt},
same bounding box=A]
\path
(-a,-a,-a) coordinate (A)
(a,-a,-a) coordinate (B)
(a,a,-a) coordinate (C)
(-a,a,-a) coordinate (D)
(-a,-a,a) coordinate (A')
(a,-a,a) coordinate (B')
(a,a,a) coordinate (C')
(-a,a,a) coordinate (D')
(a,0,-a) coordinate (K)
(a,-a,0) coordinate (M);
\tikzset{3d/define orthonormal dreibein={A={(K)},B={(D)},C={(A')}}}
\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
\path[manual pattern={lines/.style=3d/hidden}] (D) -- (A') -- (M) -- (K) -- cycle;
\end{scope}
\draw[3d/hidden] (D) -- (K);
\begin{scope}[canvas is xz plane at y=-a]
\path[manual pattern] (A') -- (M) -- (B') -- cycle;
\end{scope}
\begin{scope}[canvas is yz plane at x=a]
\path[manual pattern] (K) -- (C) -- (C') -- (B') -- (M) -- cycle;
\end{scope}
\begin{scope}[canvas is xy plane at z=a]
\path[manual pattern] (A') -- (B') -- (C') -- (D') -- cycle;
\end{scope}
\tikzset{3d/polyhedron/.cd,O={(0,0,0)},fore/.append style={fill=none},
back/.append style={3d/hidden},
draw face with corners={{(A')},{(B')},{(C')},{(D')}},
draw face with corners={{(A)},{(B)},{(M)},{(A')}},
draw face with corners={{(A')},{(M)},{(B')}},
draw face with corners={{(A)},{(D)},{(A')}},
draw face with corners={{(D)},{(D')},{(A')}},
draw face with corners={{(D)},{(D')},{(C')},{(C)}},
draw face with corners={{(K)},{(C)},{(C')},{(B')},{(M)},{(K)}},
draw face with corners={{(B)},{(K)},{(M)}}}
\path foreach \X in {A,...,D} {(\X) node[c,label={below:$\X$}]{}
(\X') node[c,label={above:$\X'$}]{}}
foreach \X in {K,M} {(\X) node[c,label={above:$\X$}]{}};
\end{tikzpicture}
\end{document}
```