In very principle it is not a hard problem. One only has to switch to an appropriate plane, and draw a circle. In this plane, the arc can be parametrized as
```
gamma(t)=(R*cos(t),R*(sin(t)) .
```
The critical values for visibility are given by
```
gamma(t).(nx,ny)=0 ,
```
where `(nx,ny)` are the x and y components of the normal of the screen. The solutions are
```
tcrit=atan2(nx,-ny) and atan2(-nx,ny) .
```
The good news is that switching to the plane and computing the normal on the screen are already built into `3dtools`. The bad news is that the corner cases are nasty, especially when one has to cure them with TeX methods.
To be specific, let us consider great circle arcs (other arcs are completely analogous). Given two points on the sphere, a great circle arc is in the plane that runs through the two points and the center of the sphere. (This works as long as the point are not antipods, in which case the great circle arc is not uniquely defined. This is one out of many corner cases, which one has to treat with TeX methods.) The following code constructs such arcs using the above strategy. For the convenience it also introduces a key that allows the user to place points at a certain latitude and longitude of a sphere of a given radius.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\makeatletter
\tikzset{3d/point on sphere/.code={\tikzset{3d/.cd,#1,
/tikz/insert path={
({\pgfkeysvalueof{/tikz/3d/R}*cos(\pgfkeysvalueof{/tikz/3d/longitude})*cos(\pgfkeysvalueof{/tikz/3d/latitude})},
{\pgfkeysvalueof{/tikz/3d/R}*sin(\pgfkeysvalueof{/tikz/3d/longitude})*cos(\pgfkeysvalueof{/tikz/3d/latitude})},
{\pgfkeysvalueof{/tikz/3d/R}*sin(\pgfkeysvalueof{/tikz/3d/latitude})})}}},
3d/latitude/.initial=0,3d/longitude/.initial=0,
3d/arcs/O/.initial={(0,0,0)},
3d/arcs/n/.initial={(0,0,1)},
3d/arcs/A/.initial={(1,0,0)},
3d/arcs/B/.initial={(0,1,0)},
pics/3d/great circle arc/.style={code={%
\tikzset{3d/arcs/.cd,#1}%
\def\pv##1{\pgfkeysvalueof{/tikz/3d/arcs/##1}}%
\pgfmathsetmacro{\pgfutil@tmpa}{tddistance("\pgfkeysvalueof{/tikz/3d/arcs/A}","\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathsetmacro{\pgfutil@tmpb}{tddistance("\pgfkeysvalueof{/tikz/3d/arcs/B}","\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{abs(\pgfutil@tmpa-\pgfutil@tmpb)<0.01?1:0}%
\ifnum\pgfutil@tmpi=0\relax
\PackageWarning{3dtools}{The points \pv{A} and \pv{B} do not sit on the
same sphere around \pv{O}.}%
\else
\pgfmathsetmacro{\pgfutil@tmpA}{TD("\pgfkeysvalueof{/tikz/3d/arcs/A}")}%
\pgfmathsetmacro{\pgfutil@tmpB}{TD("\pgfkeysvalueof{/tikz/3d/arcs/B}")}%
\pgfmathsetmacro{\pgfutil@tmpO}{TD("\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathtruncatemacro{\pgfutil@tmpV}{sign(screendepth(\pgfutil@tmpA)-screendepth(\pgfutil@tmpO))}%
\pgfmathtruncatemacro{\pgfutil@tmpW}{sign(screendepth(\pgfutil@tmpB)-screendepth(\pgfutil@tmpO))}%
\pgfmathsetmacro{\pgfutil@tmpr}{sqrt(\pgfutil@tmpa*\pgfutil@tmpb)}%
\pgfmathsetmacro{\pgfutil@tmpc}{Mod(360+acos(TD("\pv{A}-\pv{O}o\pv{B}-\pv{O}")/\pgfutil@tmpa/\pgfutil@tmpb),360)}%
\pgfmathsetmacro{\pgfutil@tmpi}{(tddistance("\pgfkeysvalueof{/tikz/3d/arcs/B}","\pgfkeysvalueof{/tikz/3d/arcs/A}")
-\pgfutil@tmpa-\pgfutil@tmpb<0.1?1:0)}%
\ifnum\pgfutil@tmpi=0\relax
\pgfmathsetmacro{\pgfutil@tmpC}{TD("\pgfkeysvalueof{/tikz/3d/arcs/A}x\pgfkeysvalueof{/tikz/3d/arcs/n}")}%
\tikzset{3d/define orthonormal dreibein={A={\pv{O}},B={\pv{A}},C={(\pgfutil@tmpC)}}}
\else
\tikzset{3d/define orthonormal dreibein={A={\pv{O}},B={\pv{A}},C={\pv{B}}}}
\fi
\fi
\tikzset{3d/arc/draw arc}
}},
/tikz/3d/arc/draw arc/.code={ \begin{scope}[x/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ex}},
y/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ey}},
z/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ez}}]
\pgfmathsetmacro{\pgfutil@tmpt}{Mod(360+atan2(-1*nscreenx,nscreeny),360)}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{(\pgfutil@tmpt>0&&\pgfutil@tmpt<\pgfutil@tmpc)+(\pgfutil@tmpt+180>0&&\pgfutil@tmpt+180<\pgfutil@tmpc)}
% \typeout{angle=\pgfutil@tmpc,radius=\pgfutil@tmpr,O=\pv{O},
% tcrit=\pgfutil@tmpt,V=\pgfutil@tmpV,W=\pgfutil@tmpW,i=\pgfutil@tmpi}
\ifcase\pgfutil@tmpi
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpa) arc[start angle=0,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\else
\path[3d/visible] (0:\pgfutil@tmpa) arc[start angle=0,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\fi
\or
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpa)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpa];
\path[3d/visible] (\pgfutil@tmpt:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\else
\path[3d/visible] (0:\pgfutil@tmpa)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpa];
\path[3d/hidden] (\pgfutil@tmpt:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\fi
\or
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpa)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpa];
\path[3d/visible] (\pgfutil@tmpt:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpt+180,radius=\pgfutil@tmpa];
\path[3d/hidden] (\pgfutil@tmpt+180:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt+180,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\else
\path[3d/visible] (0:\pgfutil@tmpa)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpa];
\path[3d/hidden] (\pgfutil@tmpt:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpt+180,radius=\pgfutil@tmpa];
\path[3d/visible] (\pgfutil@tmpt+180:\pgfutil@tmpa)
arc[start angle=\pgfutil@tmpt+180,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpa];
\fi
\fi
\end{scope}}}
\makeatother
\begin{document}
\begin{tikzpicture}[3d/install view={phi=0,theta=70},line join = round, line cap = round,
declare function={R=3;}]
\path (0,0,0) coordinate (O)
[3d/point on sphere={R=R,longitude=30,latitude=20}] coordinate (A)
[3d/point on sphere={R=R,longitude=-120,latitude=50}] coordinate (B);
\path pic{3d/great circle arc={A={(A)},B={(B)},O={(O)}}};
\draw[3d/visible,3d/screen coords] (O) circle[radius=R];
\end{tikzpicture}
\end{document}
```

The other arcs can be constucted analogously. However, to implement them one would have to agree on a given strategy to define the arc. One possible way is to specify the start and end points as well as the normal of the plane in which the arc should be. The longitude and latitude arcs are then special cases. This is a prototype.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\makeatletter
\tikzset{3d/point on sphere/.code={\tikzset{3d/.cd,#1,
/tikz/insert path={
({\pgfkeysvalueof{/tikz/3d/R}*cos(\pgfkeysvalueof{/tikz/3d/longitude})*cos(\pgfkeysvalueof{/tikz/3d/latitude})},
{\pgfkeysvalueof{/tikz/3d/R}*sin(\pgfkeysvalueof{/tikz/3d/longitude})*cos(\pgfkeysvalueof{/tikz/3d/latitude})},
{\pgfkeysvalueof{/tikz/3d/R}*sin(\pgfkeysvalueof{/tikz/3d/latitude})})}}},
3d/latitude/.initial=0,3d/longitude/.initial=0,
3d/arcs/O/.initial={(0,0,0)},
3d/arcs/n/.initial={(0,0,1)},
3d/arcs/A/.initial={(1,0,0)},
3d/arcs/B/.initial={(0,1,0)},
pics/3d/great circle arc/.style={code={%
\tikzset{3d/arcs/.cd,#1}%
\def\pv##1{\pgfkeysvalueof{/tikz/3d/arcs/##1}}%
\pgfmathsetmacro{\pgfutil@tmpa}{tddistance("\pgfkeysvalueof{/tikz/3d/arcs/A}","\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathsetmacro{\pgfutil@tmpb}{tddistance("\pgfkeysvalueof{/tikz/3d/arcs/B}","\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{abs(\pgfutil@tmpa-\pgfutil@tmpb)<0.01?1:0}%
\ifnum\pgfutil@tmpi=0\relax
\PackageWarning{3dtools}{The points \pv{A} and \pv{B} do not sit on the
same sphere around \pv{O}.}%
\else
\pgfmathsetmacro{\pgfutil@tmpA}{TD("\pgfkeysvalueof{/tikz/3d/arcs/A}")}%
\pgfmathsetmacro{\pgfutil@tmpB}{TD("\pgfkeysvalueof{/tikz/3d/arcs/B}")}%
\pgfmathsetmacro{\pgfutil@tmpO}{TD("\pgfkeysvalueof{/tikz/3d/arcs/O}")}%
\pgfmathtruncatemacro{\pgfutil@tmpV}{sign(screendepth(\pgfutil@tmpA)-screendepth(\pgfutil@tmpO))}%
\pgfmathtruncatemacro{\pgfutil@tmpW}{sign(screendepth(\pgfutil@tmpB)-screendepth(\pgfutil@tmpO))}%
\pgfmathsetmacro{\pgfutil@tmpr}{sqrt(\pgfutil@tmpa*\pgfutil@tmpb)}%
\pgfmathsetmacro{\pgfutil@tmpc}{Mod(360+acos(TD("\pv{A}-\pv{O}o\pv{B}-\pv{O}")/\pgfutil@tmpa/\pgfutil@tmpb),360)}%
\pgfmathsetmacro{\pgfutil@tmpi}{(tddistance("\pgfkeysvalueof{/tikz/3d/arcs/B}","\pgfkeysvalueof{/tikz/3d/arcs/A}")
-\pgfutil@tmpa-\pgfutil@tmpb<0.1?1:0)}%
\begingroup
\ifnum\pgfutil@tmpi=0\relax
\pgfmathsetmacro{\pgfutil@tmpC}{TD("\pgfkeysvalueof{/tikz/3d/arcs/A}x\pgfkeysvalueof{/tikz/3d/arcs/n}")}%
\tikzset{3d/define orthonormal dreibein={A={\pv{O}},B={\pv{A}},C={(\pgfutil@tmpC)}}}%
\typeout{May not properly work yet.}%
\else
\tikzset{3d/define orthonormal dreibein={A={\pv{O}},B={\pv{A}},C={\pv{B}}}}
\fi
\endgroup
\edef\pgfutil@tmpp{0}%
\tikzset{3d/arc/draw arc}
\fi
}},
pics/3d/circle arc/.style={code={%
\tikzset{3d/arcs/.cd,#1}%
\def\pv##1{\pgfkeysvalueof{/tikz/3d/arcs/##1}}%
\pgfmathsetmacro{\pgfutil@tmpa}{tddistance("\pv{A}","\pv{O}")}%
\pgfmathsetmacro{\pgfutil@tmpb}{tddistance("\pv{B}","\pv{O}")}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{abs(\pgfutil@tmpa-\pgfutil@tmpb)<0.01?1:0}%
\ifnum\pgfutil@tmpi=0\relax
\PackageWarning{3dtools}{The points \pv{A} and \pv{B} do not sit on the
same sphere around \pv{O}.}%
\else
\pgfmathsetmacro{\pgfutil@tmpA}{TD("\pv{A}")}%
\pgfmathsetmacro{\pgfutil@tmpB}{TD("\pv{B}")}%
\pgfmathsetmacro{\pgfutil@tmpO}{TD("\pv{O}")}%
\pgfmathsetmacro{\pgfutil@tmpn}{TDunit("\pv{n}")}%
\pgfmathsetmacro{\pgfutil@tmpp}{TD("(\pgfutil@tmpn)o\pv{A}")}%
\pgfmathsetmacro{\pgfutil@tmpq}{TD("(\pgfutil@tmpn)o\pv{B}")}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{abs(\pgfutil@tmpp-\pgfutil@tmpq)<0.01?1:0}%
\ifnum\pgfutil@tmpi=0\relax
\PackageWarning{3dtools}{The points \pv{A} and \pv{B} are not located on
the sphere around \pv{O} in such a way that the normal \pv{n} can be used
to define an arc.}%
\else
\pgfmathsetmacro{\pgfutil@tmpX}{TD("\pv{A}-\pv{O}x\pv{B}-\pv{O}")}%
\pgfmathsetmacro{\pgfutil@tmpx}{TD("(\pgfutil@tmpX)o(\pgfutil@tmpX)")}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{(\pgfutil@tmpx<0.02?0:1)}%
\ifnum\pgfutil@tmpi=0\relax
\pgfmathsetmacro{\pgfutil@tmpC}{TD("\pv{A}-\pv{O}x(\pgfutil@tmpn)")}%
\else
\let\pgfutil@tmpC\pgfutil@tmpB
\fi
\pgfmathsetmacro{\pgfutil@tmpD}{TD("\pv{O}+\pgfutil@tmpp*(\pgfutil@tmpn)")}%
%\typeout{\pgfutil@tmpp,\pgfutil@tmpq,(D)=(\pgfutil@tmpD)}%
\pgfmathtruncatemacro{\pgfutil@tmpV}{sign(screendepth(\pgfutil@tmpA)-screendepth(\pgfutil@tmpO))}%
\pgfmathtruncatemacro{\pgfutil@tmpW}{sign(screendepth(\pgfutil@tmpB)-screendepth(\pgfutil@tmpO))}%
\pgfmathsetmacro{\pgfutil@tmpr}{sqrt(TD("\pv{A}-(\pgfutil@tmpD)o\pv{A}-(\pgfutil@tmpD)"))}%
\pgfmathsetmacro{\pgfutil@tmpc}{Mod(360+acos(TD("\pv{A}-(\pgfutil@tmpD)o\pv{B}-(\pgfutil@tmpD)")/\pgfutil@tmpr/\pgfutil@tmpr),360)}%
%\typeout{A=(\pgfutil@tmpA),B=(\pgfutil@tmpB),D=(\pgfutil@tmpD)}%
\begingroup
\tikzset{3d/define orthonormal dreibein={B={\pv{A}},
A={(\pgfutil@tmpD)},C/.expanded={(\pgfutil@tmpC)}}}%
\endgroup
\pgfmathsetmacro{\pgfutil@tmpp}{TD("\pgfkeysvalueof{/tikz/3d/aux keys/ez}o(\pgfutil@tmpA)")}
\tikzset{3d/arc/draw arc}
\fi
\fi
}},
/tikz/3d/arc/draw arc/.code={\begin{scope}[shift={(\pgfutil@tmpO)},
x/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ex}},
y/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ey}},
z/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ez}}]
\pgfmathsetmacro{\pgfutil@tmpt}{min(Mod(360+atan2(-1*nscreenx,nscreeny),360),Mod(540+atan2(-1*nscreenx,nscreeny),360))}%
\pgfmathsetmacro{\pgfutil@tmpu}{max(Mod(360+atan2(-1*nscreenx,nscreeny),360),Mod(540+atan2(-1*nscreenx,nscreeny),360))}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{(\pgfutil@tmpt>0&&\pgfutil@tmpt<\pgfutil@tmpc)+(\pgfutil@tmpu>0&&\pgfutil@tmpu<\pgfutil@tmpc)}%
%\typeout{i=\pgfutil@tmpi, t=\pgfutil@tmpt, u=\pgfutil@tmpu,
% c=\pgfutil@tmpc, p=\pgfutil@tmpp, V=\pgfutil@tmpV,W=\pgfutil@tmpW}
\begin{scope}[canvas is xy plane at z=\pgfutil@tmpp]
\ifcase\pgfutil@tmpi
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpr) arc[start angle=0,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\else
\path[3d/visible] (0:\pgfutil@tmpr) arc[start angle=0,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\fi
\or
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpr)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpr];
\path[3d/visible] (\pgfutil@tmpt:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\else
\path[3d/visible] (0:\pgfutil@tmpr)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpr];
\path[3d/hidden] (\pgfutil@tmpt:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\fi
\or
\ifnum\pgfutil@tmpV<0
\path[3d/hidden] (0:\pgfutil@tmpr)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpr];
\path[3d/visible] (\pgfutil@tmpt:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpu,radius=\pgfutil@tmpr];
\path[3d/hidden] (\pgfutil@tmpu:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpu,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\else
\path[3d/visible] (0:\pgfutil@tmpr)
arc[start angle=0,end angle=\pgfutil@tmpt,radius=\pgfutil@tmpr];
\path[3d/hidden] (\pgfutil@tmpt:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpt,end angle=\pgfutil@tmpu,radius=\pgfutil@tmpr];
\path[3d/visible] (\pgfutil@tmpu:\pgfutil@tmpr)
arc[start angle=\pgfutil@tmpu,end angle=\pgfutil@tmpc,radius=\pgfutil@tmpr];
\fi
\fi
\end{scope}
\end{scope}}}
\makeatother
\begin{document}
\begin{tikzpicture}[3d/install view={phi=-30,psi=0,theta=70},line join = round, line cap = round,
declare function={R=3;}]
\path (0,0,0) coordinate (O)
[3d/point on sphere={R=R,longitude=30,latitude=20}] coordinate (A)
[3d/point on sphere={R=R,longitude=-120,latitude=50}] coordinate (B)
[3d/point on sphere={R=R,longitude=-110,latitude=20}] coordinate (C);
\path pic{3d/great circle arc={A={(A)},B={(B)},O={(O)}}};
\path pic{3d/circle arc={A={(A)},B={(C)},O={(O)},n={(0,0,1)}}};
\path foreach \X in {A,B,C} {(\X)node[circle,fill,inner sep=1pt]{}};
\draw[3d/visible,3d/screen coords] (O) circle[radius=R];
\end{tikzpicture}
\begin{tikzpicture}[3d/install view={phi=-30,psi=0,theta=70},
line join = round, line cap = round,
declare function={R=3;}]
\path (0,0,0) coordinate (O)
[3d/point on sphere={R=R,longitude=30,latitude=20}] coordinate (A)
[3d/point on sphere={R=R,longitude=-120,latitude=50}] coordinate (B)
[3d/point on sphere={R=R,longitude=-110,latitude=20}] coordinate (C);
\path pic{3d/great circle arc={A={(A)},B={(B)},O={(O)}}};
\path pic{3d/circle arc={A={(A)},B={(C)},O={(O)},n={(0,0,1)}}};
\draw[3d/visible,3d/screen coords] (O) circle[radius=R];
\path (R,0,0) coordinate[label=above:{$M$}](M)
(0,0,-R) coordinate[label=above:{$N$}] (N)
(O) pic{3d/circle arc={A={(M)},B={(N)},O={(O)},n={(0,1,0)}}};
\path foreach \X in {A,B,C,M,N} {(\X)node[circle,fill,inner sep=1pt]{}};
\end{tikzpicture}
\begin{tikzpicture}[3d/install view={phi=-30,psi=0,theta=70} ,line join = round, line cap = round,
declare function={R=3;}]
\path (0,0,0) coordinate (O)
[3d/point on sphere={R=R,longitude=30,latitude=20}] coordinate (A)
[3d/point on sphere={R=R,longitude=-120,latitude=50}] coordinate (B)
[3d/point on sphere={R=R,longitude=-110,latitude=20}] coordinate (C);
\path pic{3d/great circle arc={A={(A)},B={(B)},O={(O)}}};
\path pic{3d/circle arc={A={(A)},B={(C)},O={(O)},n={(0,0,1)}}};
\draw[3d/visible,3d/screen coords] (O) circle[radius=R];
\path (0,0,R) coordinate[label=above:{$M$}](M)
(0,0,-R) coordinate[label=above:{$N$}] (N)
(O) pic{3d/circle arc={A={(M)},B={(N)},O={(O)},n={(1,0,0)}}};
\path foreach \X in {A,B,C,M,N} {(\X)node[circle,fill,inner sep=1pt]{}};
\end{tikzpicture}
\end{document}
```
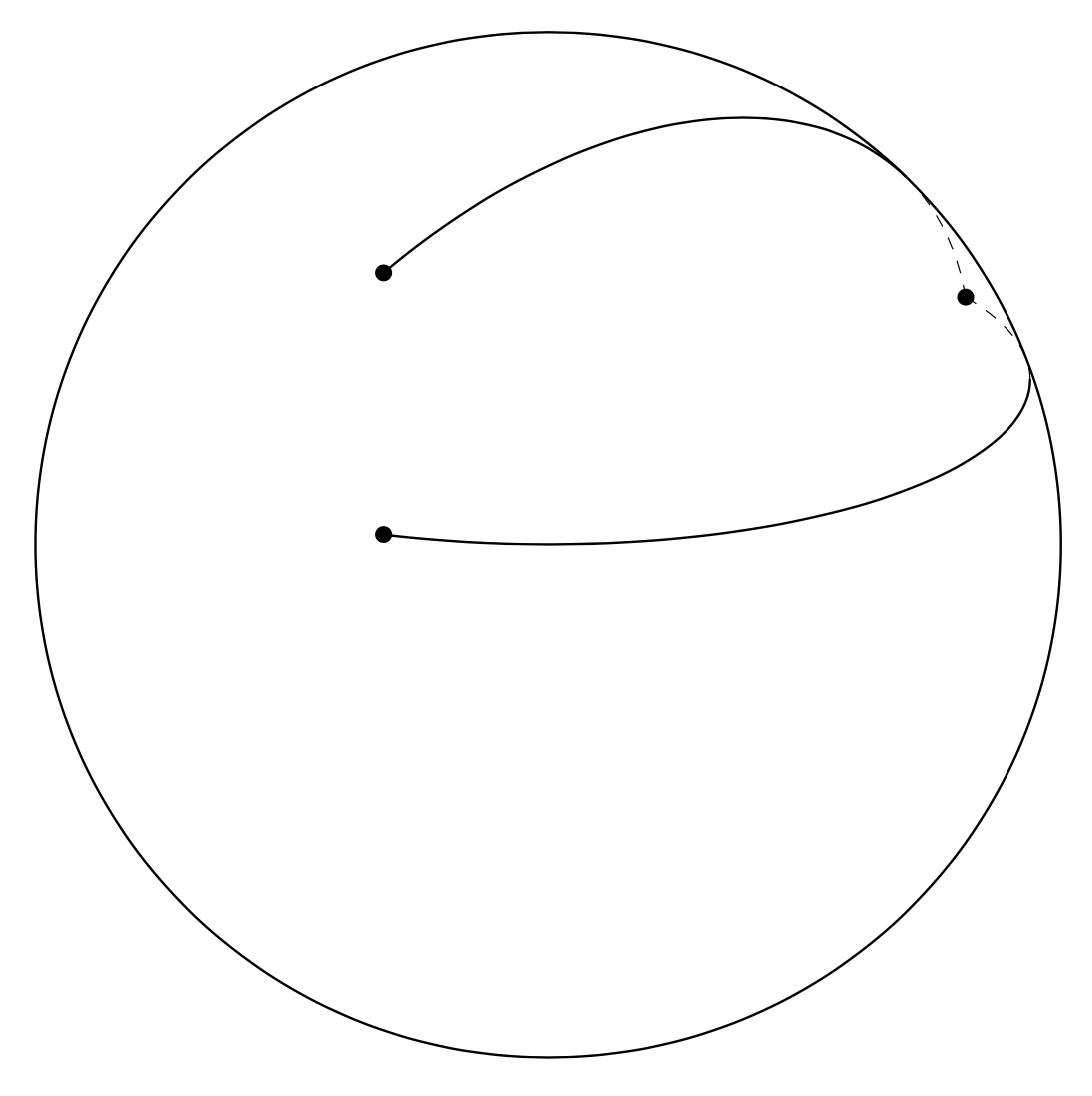
However, I will hesitate to add those until the usage and scope become clearer. It is nontrivial to come up with a usage that is useful, convenient and general enough to allow users to do what they want. So this definitely requires some more thought and inputs.