Although I shared my ConTeXt/MetaPost solution in the chat and marmot magnificently [adapted part of it in TikZ](https://topanswers.xyz/tex?q=1719#a1940), I'll post a cleaner version for LaTeX (1) so it won't be lost in comments and (2) just in case any eventual MetaPost user in LaTeX may find it useful.
```
\documentclass{standalone}
\usepackage[latex,shellescape]{gmp}
%%% #1: square size 
%%% #2: angle of rotation for the naughty square (between 0 and 90).
\newcommand\foursquares[2]%
{%
\begin{mpost}[name=foursquares]
%%% Not needed in ConTeXt
path fullsquare;
fullsquare := unitsquare shifted (-center unitsquare);
%%%
numeric u; u := \the\dimexpr#1\relax;
numeric Angle; Angle := \the\numexpr#2\relax;
pair I;
path S[], C, L[], Frame;
C := fullcircle scaled (u*sqrt(10));
Frame := fullsquare scaled (u*sqrt(10));
draw Frame withcolor (0.529, 0.808, 0.922);
draw C  withcolor 1/2[blue,white];
for i=-1 upto 1:
	S[i+1] := fullsquare scaled u shifted (u*i*up);
endfor
L[1] := (origin -- down) shifted (1/4left) scaled 2u;
L[2] := L[1] shifted (u*left);
for i=1,2:
	L[i] := L[i] 
	rotatedabout(ulcorner S[0],-Angle);
endfor
I := C intersectionpoint L[2];
S[3] := unitsquare scaled u shifted (I+u*left)
	rotatedabout(I, angle(direction 1/2 of L[2]));
S[4] := S[1] shifted (u/2+xpart point 3 of S[3],0);
for i = 0,2,3,4:
	fill S[i] withcolor 1/2[red,white];
	draw S[i] withcolor red;
endfor
\end{mpost}\usempost{foursquares}%
}
\begin{document}
\foursquares{5mm}{10}\ \foursquares{5mm}{20}\ \foursquares{5mm}{30}
\end{document}
```
![148.png](/image?hash=a0186f4ee51ddd7db19e6ccb250388f5ab8905b8f434e4099f76399b510c21c4)

This draws such a picture. However, it does not answer the question how to construct the smallest circle that fits the boxes. Rather, it relies on the user selecting the three relevant coordinates.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,through}%
\tikzset{circle through 3 points/.style n args={3}{% https://tex.stackexchange.com/a/461180
insert path={let    \p1=($(#1)!0.5!(#2)$),
                    \p2=($(#1)!0.5!(#3)$),
                    \p3=($(#1)!0.5!(#2)!1!-90:(#2)$),
                    \p4=($(#1)!0.5!(#3)!1!90:(#3)$),
                    \p5=(intersection of \p1--\p3 and \p2--\p4)
                    in },
at={(\p5)},
circle through= {(#1)}
}}

\begin{document}
\begin{tikzpicture}
 \begin{scope}[local bounding box=boxes,
 	nodes={draw=red,fill=red!20,minimum size=1cm}]
  \path[rotate=15,transform shape] node (a){} (a.70) node[anchor=south] (b){}
	  (b.110) node[anchor=south] (c){};
  \path (a.north west) coordinate (p1) ++ (0,1) coordinate (p2)	 
  (b.south west) coordinate (p3)  (b.north west) coordinate (p4)
   (intersection of p1--p2 and p3--p4) node[anchor=north east] (d){}; 	 
 \end{scope}  
 \path node[draw,circle through 3 points={a.south east}{c.north east}{d.south west}]
  (C){}; 
 \draw (C.south-|C.west) rectangle (C.north-|C.east); 
\end{tikzpicture}
\end{document}
```
![Screen Shot 2021-03-31 at 10.11.48 AM.png](/image?hash=dd7db3416b7e77c09952553562dedfc540e42042beb1796e2a15fbe05dbd14de)

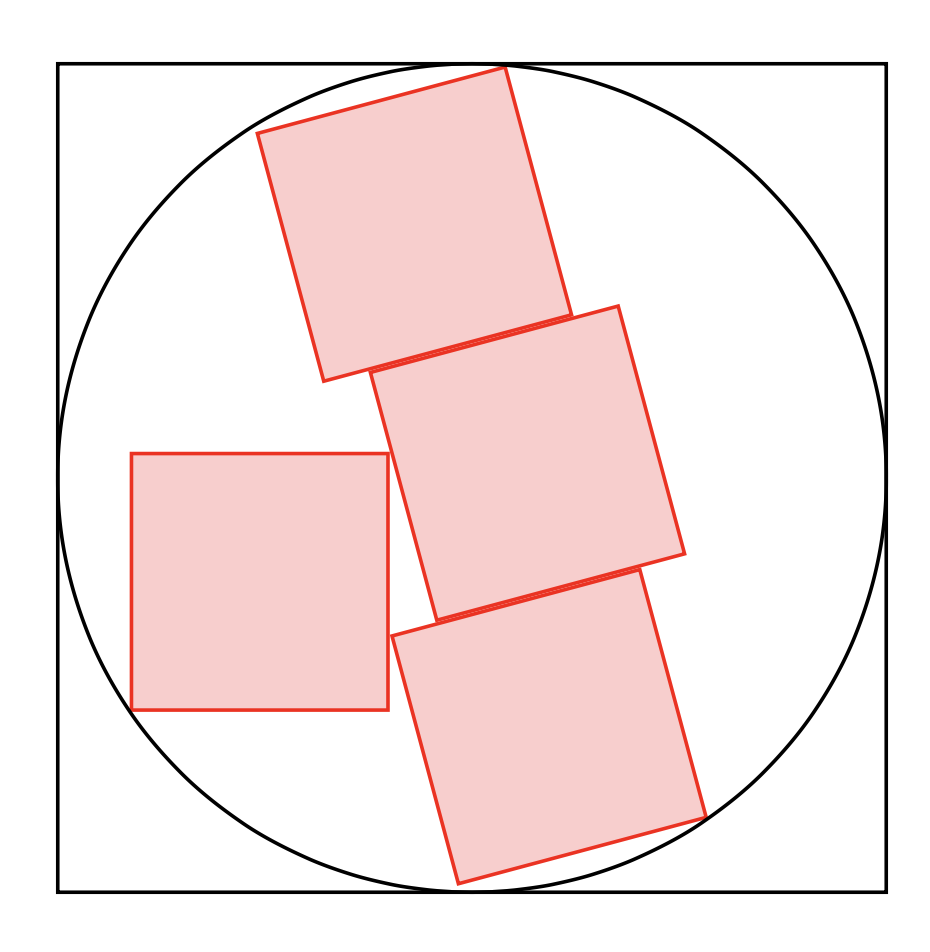
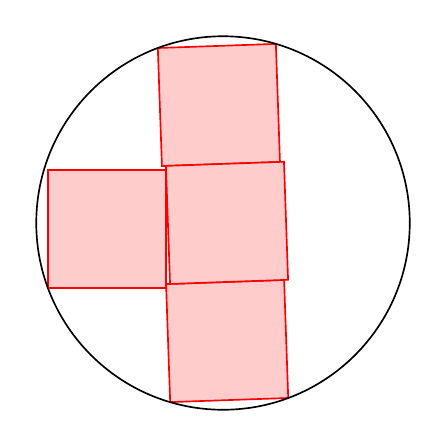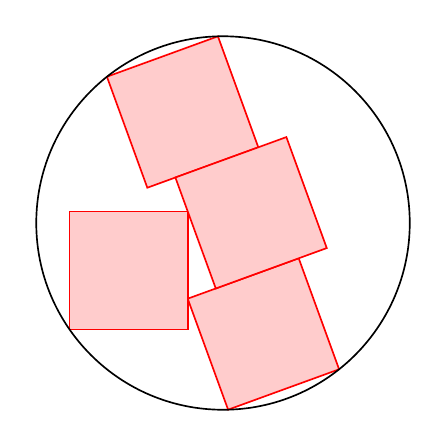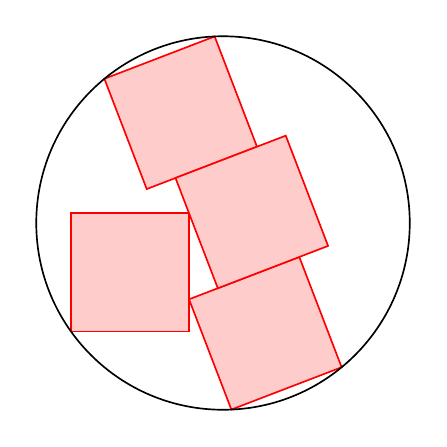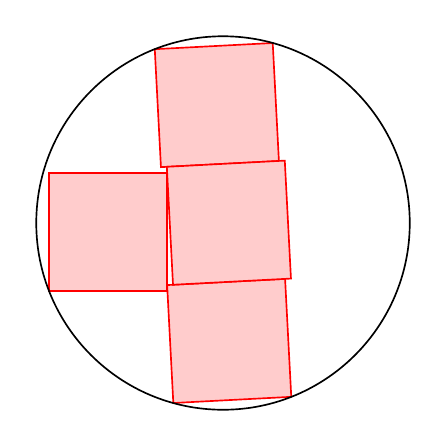
If five corners are supposed to touch the circle, there is one free parameter. The radius can be computed from the requirement that three corners of the stacked boxes (called `(a)` and `(c)` in the code below) lie on the circle, and the fourth corner is then automatically on the circle. The radius is then given by `R=sqrt(10)*a/2` (thanks to [Jairo A. del Rio](https://topanswers.xyz/transcript?room=347&id=93943#c93943)), where `a` is the length of an edge of the cube. The fourth cube, `(d)` can be rotated and moved along its edge, which determines the shift of the middle box, `(b)`. It is clear that there is a continuous parameter, and it appears likely that there is a favorable parametrization that allows one to find very simple expressions for the rotation angle as a function of the shift, say, but I did not have the passion to try to find one. So for the time being I just add an example where this relation has been guessed.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}%
\begin{document}
\begin{tikzpicture}[declare function={a=1;R=sqrt(10)*a/2;phi=15;}]
 \begin{scope}[local bounding box=boxes,
 	nodes={draw=red,fill=red!20,minimum size=a*1cm,outer sep=0pt}]
  \path[rotate=phi,transform shape] node (a){} 
  ([xshift={a*sin(4*phi/5)*1cm}]a.north) node[anchor=south] (b){}
	  ([xshift={-a*sin(4*phi/5)*1cm}]b.north) node[anchor=south] (c){};
  \path (a.north west) coordinate (p1) ++ (0,1) coordinate (p2)	 
  (b.south west) coordinate (p3)  (b.north west) coordinate (p4)
   (intersection of p1--p2 and p3--p4) node[anchor=north east] (d){}; 	 
 \end{scope}  
 \draw ($(a)!0.5!(c)$) circle[radius=R];
\end{tikzpicture}
\end{document}
```
![Screen Shot 2021-04-01 at 8.35.24 AM.png](/image?hash=8ede6ad1419d2b2798ef7a97a2e96e06dc28f53a5e968eb07e90070c382913b0)

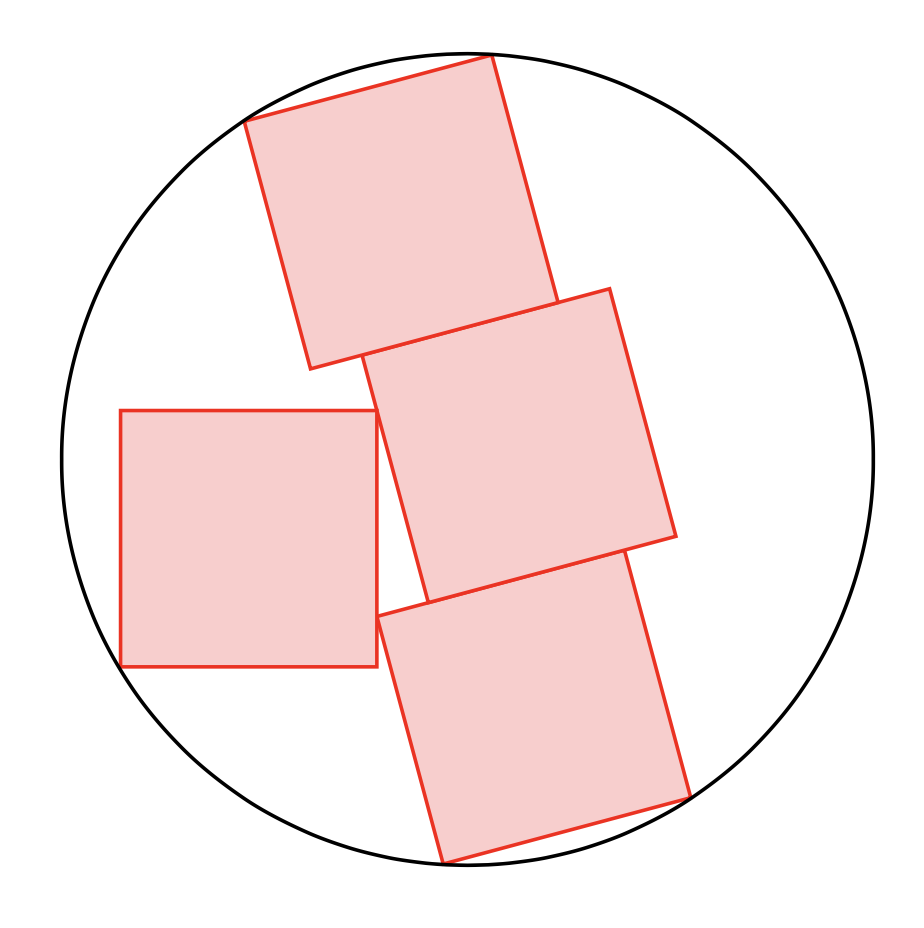
Essentially copying the strategy from [Jairo A. del Rio](https://topanswers.xyz/transcript?room=347&id=93943#c93943), one can then draw the figure in a single path. The intersections of the lines with the circle are computed analytically, hence the `atan2` and the `acos`, and the others with `calc`, which also allows us to add some useful projections. `phi` is the angle by which the stacked boxes get rotated, which we take to be the free parameter of this setup.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}%
\begin{document}
\foreach \Angle in {2,...,30,29,28,...,3}
{\begin{tikzpicture}[declare function={a=1;d=0.1;R=sqrt(10)*a/2;
	phi0=atan2(1,3);phi=\Angle;}]
 \draw[nodes={draw=red,fill=red!20,minimum size=a*1cm,outer sep=0pt}]
  (-90-phi0+phi:R) node[anchor=south west,rotate=phi](a){}
  (90+phi0+phi:R) node[anchor=north west,rotate=phi](c){}
  let \p1=(a.north west),\n1={acos((a*1cm-\x1)/(R*1cm))} in
  (180+\n1:R) node[anchor=south west](d){}
  ($(a.north west)!(d.north east)!(a.north east)$)
  node[anchor=south west,rotate=phi](b){}	
  (0,0) circle[radius=R];
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=cf23e79734eef85728eec32a26e0a0299298ba8348dca6e4dbbf917720338a51)