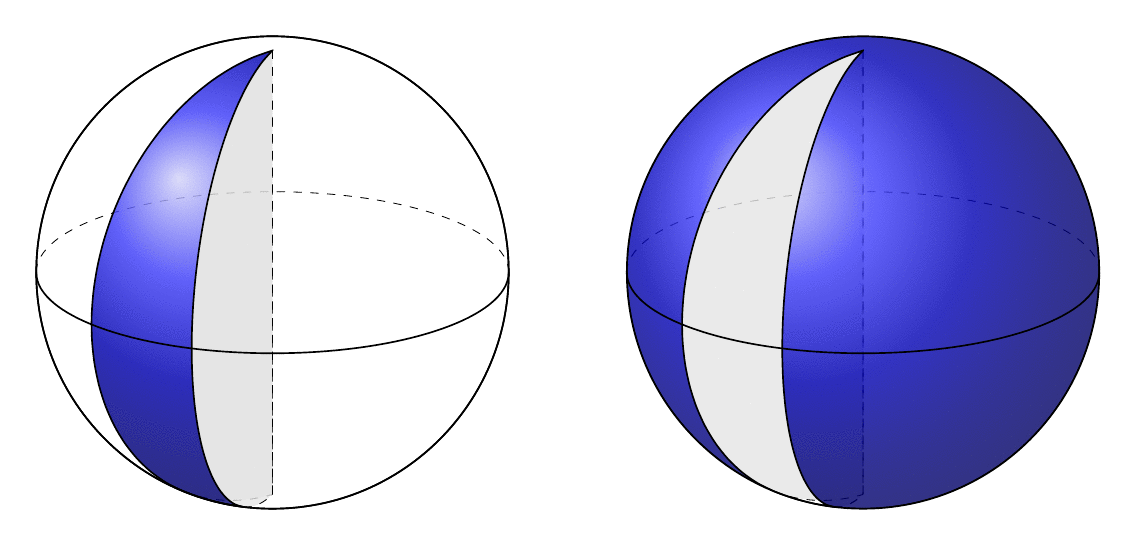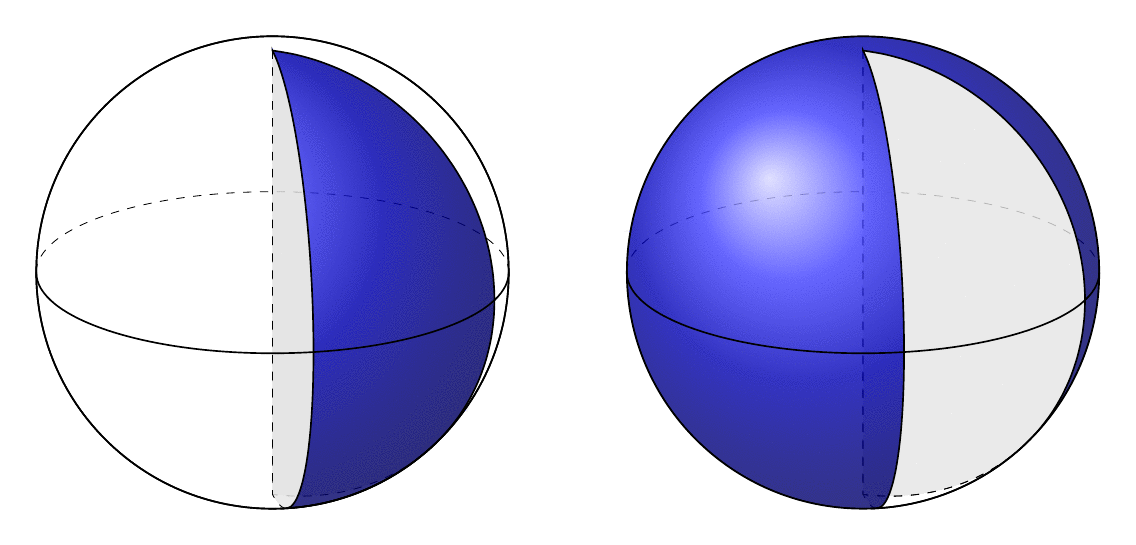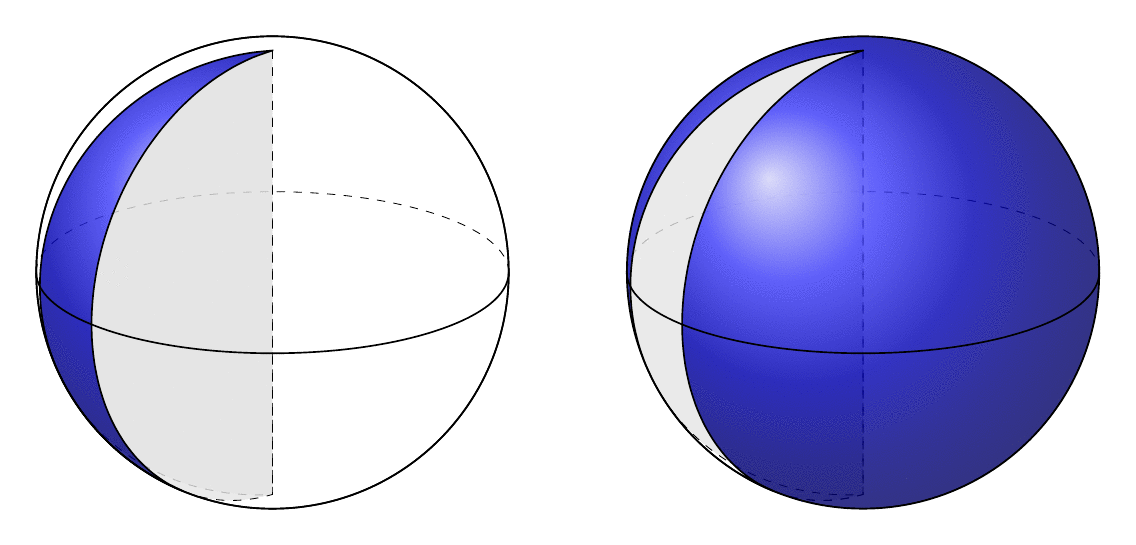
This one is not (yet?) fully rotatable but computes the relevant critical angles. The problem with both of the screen shots posted in the question is either the horizontal circle is not the equator, or the corners of the wedge are not the poles. If the poles are at the uppermost and lowermost points of the circle representing the sphere, the equator is just a horizontal line.
This code provides you with a consistent orthonormal projection, but has only been tested for certain ranges of the view angles. Also, `alpha` needs to be greater than `beta`, but this is just a convention (rather than a restriction).
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,decorations.pathreplacing,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\foreach \myalpha/\mybeta in {0/-30,90/30,-30/-60}
{\begin{tikzpicture}[
%declare function={R=2;alpha=0;beta=-30;},
%declare function={R=2;alpha=90;beta=30;},
declare function={R=2;alpha=\myalpha;beta=\mybeta;},
compute critical angles/.code={
% critical angles
\pgfmathtruncatemacro{\itest}{nscreenz<0?0:1}
\ifnum\itest=0
\pgfmathsetmacro{\tcritA}{atan2(nscreenx*cos(alpha)+nscreeny*sin(alpha),-1*nscreenz)}
\pgfmathsetmacro{\tcritB}{atan2(nscreenx*cos(beta)+nscreeny*sin(beta),-1*nscreenz)}
\edef\tmin{90}
\edef\tmax{-90}
\else
\pgfmathsetmacro{\tcritA}{atan2(nscreenx*cos(alpha)+nscreeny*sin(alpha),-1*nscreenz)-180}
\pgfmathsetmacro{\tcritB}{atan2(nscreenx*cos(beta)+nscreeny*sin(beta),-1*nscreenz)-180}
\edef\tmin{-90}
\edef\tmax{90}
\fi
\path ({R*cos(alpha)*cos(\tcritA)},{R*sin(alpha)*cos(\tcritA)},{R*sin(\tcritA)})
coordinate (pA)
({R*cos(beta)*cos(\tcritB)},{R*sin(beta)*cos(\tcritB)},{R*sin(\tcritB)})
coordinate (pB);
\pgfmathtruncatemacro{\mysign}{\pgfkeysvalueof{/tikz/3d/wedge/complement}==1?1:-1}
\pgfmathtruncatemacro{\itest}{screendepth(cos(alpha+\mysign*90),sin(alpha+\mysign*90),0)<0?0:1}
\ifnum\itest=1
\path[fill=gray!20,smooth] plot[variable=\t,domain=90:-90]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)});
\draw[3d/hidden,smooth] plot[variable=\t,domain=\tcritA:\tmin]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}) --
(0,0,{sign(\tmax)*R});
\else
\path[fill=gray!20,smooth,on layer=background] plot[variable=\t,domain=90:-90]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)});
\draw[3d/hidden,smooth,on layer=background] plot[variable=\t,domain=\tcritA:\tmin]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}) --
(0,0,{sign(\tmax)*R});
\fi
\pgfmathtruncatemacro{\itest}{screendepth(cos(beta-\mysign*90),sin(beta-\mysign*90),0)<0?0:1}
\ifnum\itest=1
\path[fill=gray!20,smooth] plot[variable=\t,domain=90:-90]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)});
\draw[3d/hidden,smooth] plot[variable=\t,domain=\tcritB:\tmin]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)}) --
(0,0,{sign(\tmax)*R});
\else
\path[fill=gray!20,smooth,on layer=background] plot[variable=\t,domain=90:-90]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)});
\draw[3d/hidden,smooth,on layer=background] plot[variable=\t,domain=\tcritB:\tmin]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)}) --
(0,0,{sign(\tmax)*R});
\fi
},3d/wedge/.cd,complement/.initial=0,
/tikz/.cd,fill opacity=0.8]
%
\begin{scope}[3d/install view={phi=110,psi=0,theta=70}]
\tikzset{3d/wedge/complement=1,compute critical angles}
\path[save named path=wedge,smooth] plot[variable=\t,domain=\tcritA:\tmax]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)})
-- plot[variable=\t,domain=\tmax:\tcritB]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)})
[3d/screen coords] let \p1=(pA),\p2=(pB),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} in
arc[start angle=\n2,end angle=\n1,radius=R];
\path[3d/visible,3d/screen coords] circle[radius=R];
\begin{scope}
\clip[use named path=wedge];
\path[3d/visible,3d/screen coords,ball color=blue] circle[radius=R];
\end{scope}
\draw[use named path=wedge];
\draw[3d/visible,3d/screen coords] circle[radius=R];
\draw[3d/hidden/.append style={on layer=background}]
pic{3d/circle on sphere={R=2,n={(0,0,1)}}};
\end{scope}
%
\begin{scope}[3d/install view={phi=110,psi=0,theta=70},xshift=5cm]
\tikzset{compute critical angles}
\draw[3d/hidden,smooth] plot[variable=\t,domain=\tcritA:\tmin]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}) --
(0,0,{sign(\tmax)*R});
\path[save named path=wedge,smooth] plot[variable=\t,domain=\tcritA:\tmax]
({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)})
-- plot[variable=\t,domain=\tmax:\tcritB]
({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)})
[3d/screen coords] let \p1=(pA),\p2=(pB),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} in
arc[start angle=\n2,end angle=\n1,radius=R];
\begin{scope}
\clip[even odd clip,3d/screen coords,use named path=wedge] circle[radius=R];
\path[3d/visible,3d/screen coords,ball color=blue] circle[radius=R];
\end{scope}
\draw[use named path=wedge];
\draw[3d/visible,3d/screen coords] circle[radius=R];
\draw[3d/hidden/.append style={on layer=background}]
pic{3d/circle on sphere={R=2,n={(0,0,1)}}};
\end{scope}
\end{tikzpicture}}
\end{document}
```