Intersection of a plane and a cylinder
add tag
Anonymous 1123 
Before, I used 2D to draw some figures. This is a intersection of a plane and a cylinder.
```
\documentclass[border=2mm]{standalone}
\usepackage{fouriernc}
\usepackage{tikz}
\usepackage{tkz-euclide}
\usetikzlibrary{shadings}
\begin{document}
\begin{tikzpicture}
\def\R{2}
\def\a{0.5}
\def\h{2*\R}
(\R,0) -- (\R,\h)  arc (360:180:\R cm and \a cm)
          -- (-\R,0) arc (180:360:\R cm and \a cm);

(0,\h) circle (\R cm and \a cm);
  \draw[thick] (-\R,\h) -- (-\R,0) arc (180:360:\R cm and \a cm)-- (\R,\h) ++ (-\R,0) circle (\R cm and \a cm);
  \draw[dashed] (-\R,0) arc (180:0:\R cm and \a cm);
\coordinate (B) at (0,0);
\coordinate (A) at ($(B)+(0,\h)$);
\coordinate (G) at (-\R,0);
\coordinate (H) at (\R,0);
\coordinate (C) at ($(B) + (225:{\R} and {\a})$);
\coordinate (D) at ($(C)+(0,\h)$);
\coordinate (E) at ($(B)-(C)$);
\coordinate (F) at ($2*(A)-(D)$);
\tkzFillPolygon[pattern=north west lines](C,D,F,E)
\tkzDrawSegments[thick](F,D D,C)
\tkzDrawSegments[dashed](A,B E,C E,F)
\tkzDrawPoints[fill = black,size = 2 pt](A,B,C,D,E,F)
\tkzLabelPoints[above](A,D,F)
\tkzLabelPoints[below](C,B,E)
 \end{tikzpicture}
\end{document}
```
![ScreenHunter 41.png](/image?hash=f537038524525370fa16bfb9e0089db579c37e672407636836c6bebf44190f50)

How about draw intersection of a plane and a cylinder in 3D?
Top Answer
user 3.14159 
Here is a way. At some point I may add a cylinder pic, or upgrate the frustum to allow for two equal radii. 
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,patterns.meta,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[declare function={R=2;h=2*R;alpha=30;}]
 \begin{scope}[3d/install view={phi=0,psi=0,theta=70}]
  \draw[3d/hidden] (R,0,0) arc[start angle=0,end angle=180,radius=R];
  \path[every coordinate node/.append style={circle,inner sep=1pt,fill}] 
  	(alpha:R) coordinate[label=below:{$E$}] (E) (alpha+180:R) coordinate[label=below:{$C$}] (C)
    (0,0,0) coordinate[label=below:{$B$}] (B) (0,0,h) coordinate[label=above:{$A$}] (A)
   [shift={(A)}] (alpha:R) coordinate[label=above:{$F$}] (F) (alpha+180:R) coordinate[label=above:{$D$}] (D);
  \draw[3d/hidden] (A) -- (B) (C) -- (E) -- (F); 
  \path[pattern={Lines[angle=-45,distance={2pt}]}] 
   (C.center) -- (D.center) -- (F.center) -- (E.center) -- cycle;
  \draw[3d/visible] (C) -- (D) -- (F); 
  \draw[3d/visible] (R,0,h) -- (R,0,0) arc[start angle=0,end angle=-180,radius=R]
   -- (-R,0,h) (0,0,h) circle[radius=R];
 \end{scope}
\end{tikzpicture}
\end{document}
```
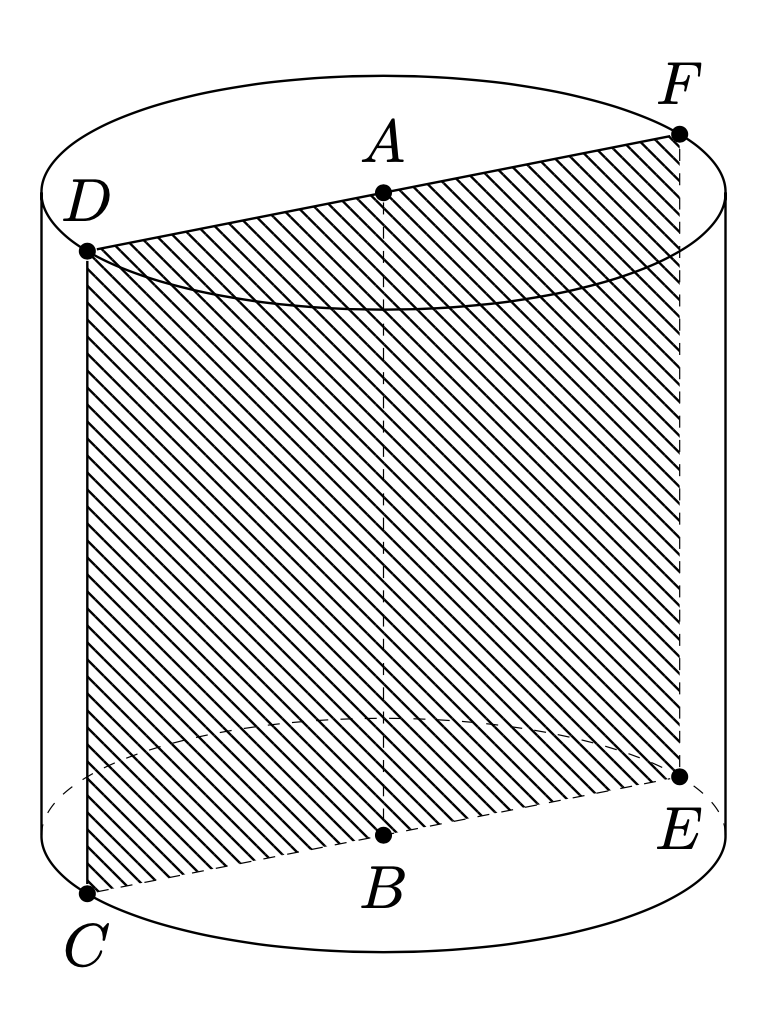
![Screen Shot 2021-03-19 at 9.26.23 PM.png](/image?hash=0f6b622a6de985d6a88125a05c0fa3be647ec66411b0c09dafd7e423877bdba8)

**ADDENDUM**: I added the frustum with two equal radii, i.e. a cylinder, to `3dtools`. Now one can draw intersections of planes with cylinders. The following is a *start*, i.e. I did not implement all cases in full detail, let alone test them thoroughly. The following depicts the "generic" case.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,patterns.meta,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[declare function={R=2;h=2*R;}]
 \begin{scope}[3d/install view={phi=0,psi=0,theta=70}]
  \path (0,0,h/2) coordinate (P);
  \pgfmathsetmacro{\myPx}{TD("(P)o(1,0,0)")}
  \pgfmathsetmacro{\myPy}{TD("(P)o(0,1,0)")}
  \pgfmathsetmacro{\myPz}{TD("(P)o(0,0,1)")}
  % in principle we would have to check that (P) is not outside the cylinder
  \path[overlay] (0,0,1) coordinate (n);
  \path[overlay] (1,1,0) coordinate (n);
  \path[overlay] (1,1,1) coordinate (n);
  \pgfmathsetmacro{\mynx}{TD("(n)o(1,0,0)")}
  \pgfmathsetmacro{\myny}{TD("(n)o(0,1,0)")}
  \pgfmathsetmacro{\mynz}{TD("(n)o(0,0,1)")}
  \pgfmathtruncatemacro{\itest}{(abs(\mynx)+abs(\myny)>0.01?1:0)+(abs(\mynz)>0.01?2:0)}
  \ifcase\itest
   \typeout{Normal is too short.}
  \or
   % normal is in the x-y plane
   \pgfmathsetmacro{\myex}{TDunit("(0,0,1)")}
   \pgfmathsetmacro{\myey}{TDunit("(n)x(0,0,1)")}
   \pgfmathsetmacro{\mynn}{TDunit("(n)")}
   \pgfmathsetmacro{\mys}{TD("(\mynn)o(\myPx,\myPy,0)")}
   \pgfmathsetmacro{\myS}{TD("\mys*(\mynn)")}
   \path[overlay] (\myex) coordinate (myex) (\myey) coordinate (myey)
   	(\myS) coordinate (myS);
   \begin{scope}[x={(myex)},y={(myey)},shift={(myS)}]
    \pgfmathsetmacro{\myr}{sqrt(R*R-\mys*\mys)}
	\path[pattern={Lines[angle=-45,distance={2pt}]}] 
	 (0,-\myr) -- (0,\myr) -- (h,\myr) -- (h,-\myr) -- cycle;
   \end{scope}
  \or
   % normal is in the z direction
   \pgfmathsetmacro{\mynn}{TDunit("(n)")}
   \tikzset{3d/plane with normal={(\mynn) through (P) named pI},
   	3d/line through={(0,0,0) and (0,0,h) named lC}}
   \path[3d/intersection of={lC with pI}] coordinate (myS);	
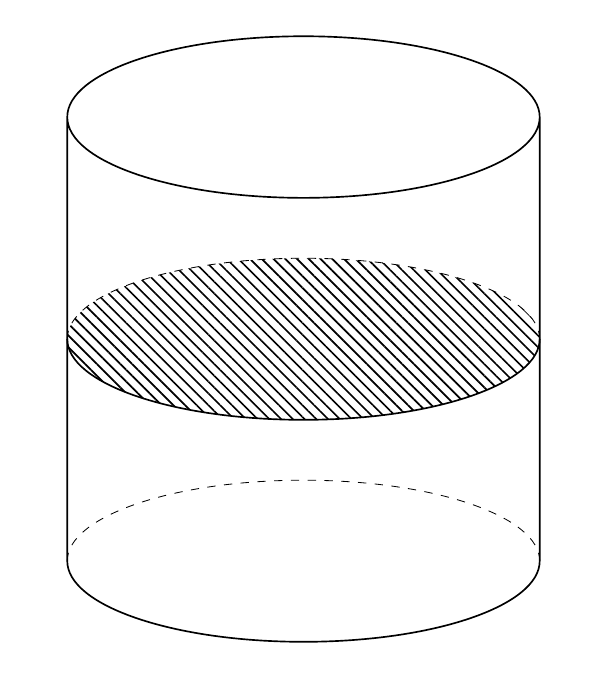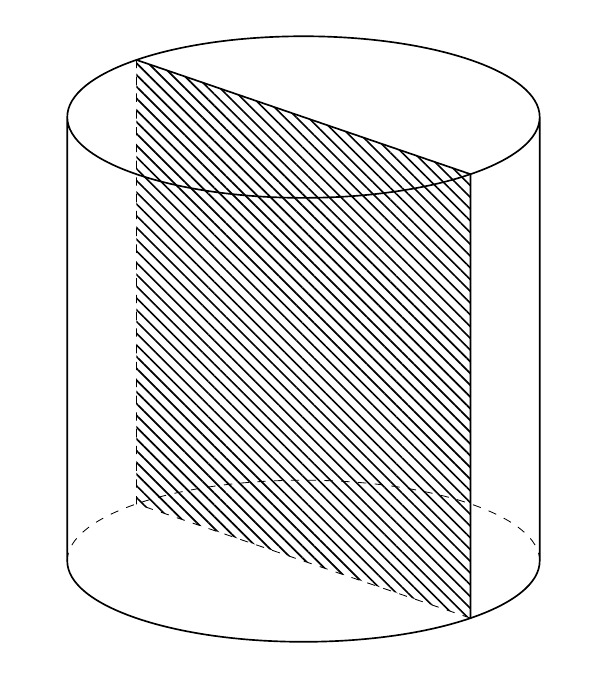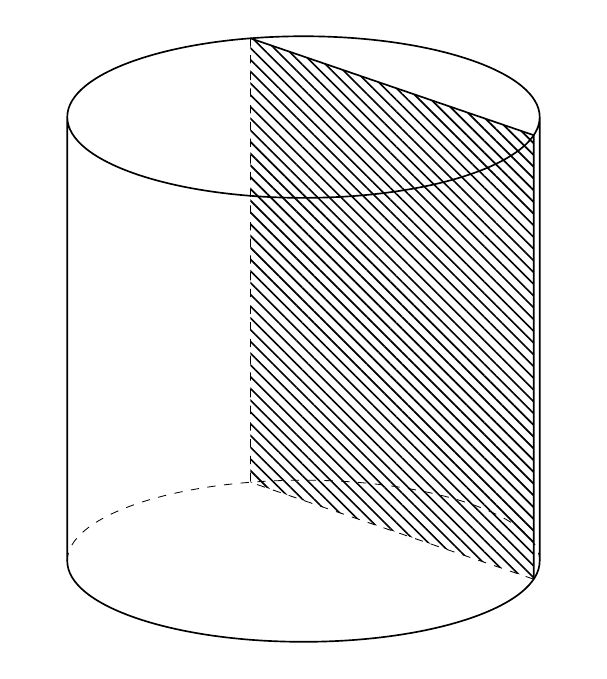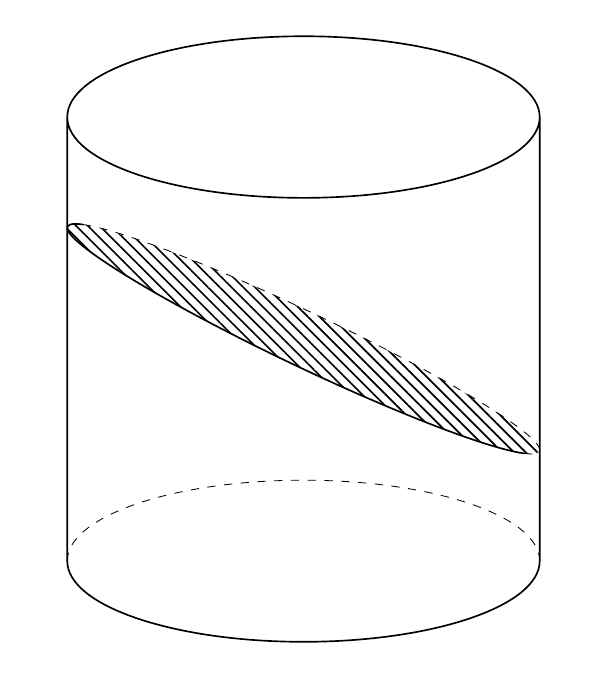
   \path[pattern={Lines[angle=-45,distance={2pt}]}] (myS) circle[radius={R}];
  \or
   % normal is generic
   \pgfmathsetmacro{\mynn}{TDunit("(n)")}
   \tikzset{3d/plane with normal={(\mynn) through (P) named pI},
   	3d/line through={(0,0,0) and (0,0,h) named lC}}
   \path[3d/intersection of={lC with pI}] coordinate (myS);	
   \pgfmathsetmacro{\mynnz}{TD("(\mynn)o(0,0,1)")}
   \pgfmathsetmacro{\myangle}{asin(\mynnz)}
   \pgfmathsetmacro{\myangleB}{asin(TD("(\mynn)o(1,0,0)"))}
   \pgfmathsetmacro{\myey}{TDunit("(n)x(0,0,1)")}
   \path[overlay] (\mynn) coordinate (myex) (\myey) coordinate (myey);
   \begin{scope}[x={(myex)},y={(myey)},shift={(myS)}]
	\draw[3d/hidden]  (\myangleB:{R/cos(\myangle)} and {R})
	 arc[start angle=\myangleB,end angle=\myangleB-180,
	 	x radius={R/cos(\myangle)},y radius={R}];
	\path[pattern={Lines[angle=-45,distance={2pt}]}] 
	 circle[x radius={R/cos(\myangle)},y radius={R}];
	\draw[3d/visible]  (\myangleB:{R/cos(\myangle)} and {R})
	 arc[start angle=\myangleB,end angle=\myangleB+180,
	 	x radius={R/cos(\myangle)},y radius={R}];
   \end{scope}
  \fi 
  \pic{3d/frustum={r=R,R=R,h=h}};
 \end{scope}
\end{tikzpicture}
\end{document}
```
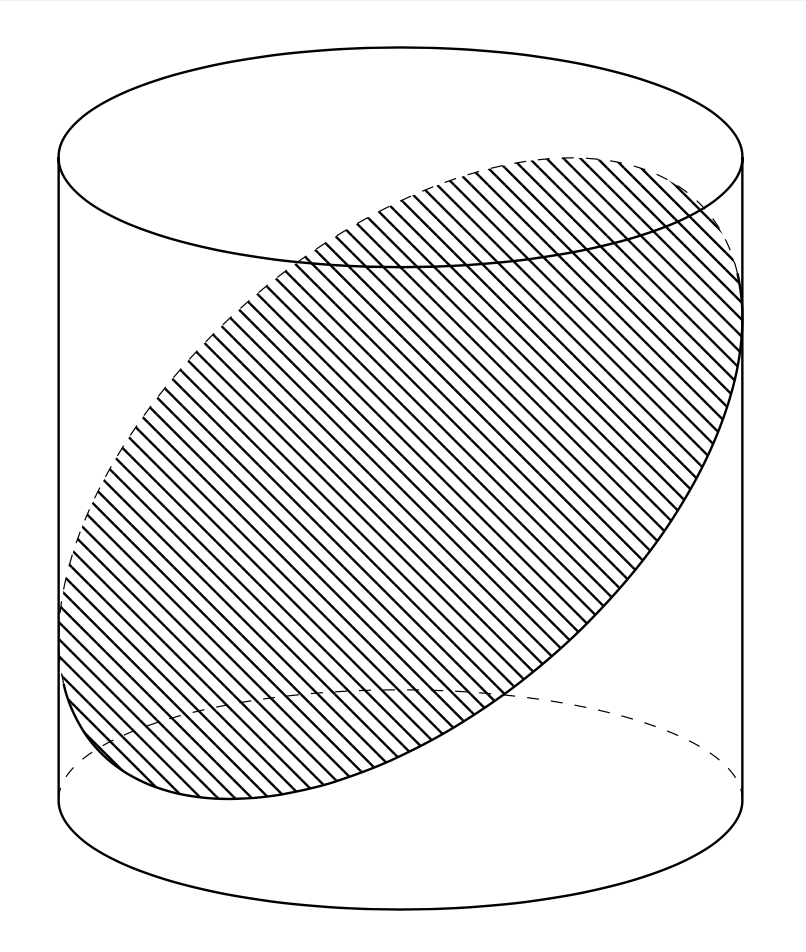
![Screen Shot 2021-03-20 at 9.12.09 AM.png](/image?hash=4bf74e1aaace70f521b955ddc6076c70c3f9535a3615d791b965f015ea794cdb)
As you can see, one would have to make all sorts of sanity checks for the user input. Doable, but tedious.

This version makes a few more checks, but there is a small inaccuracy in the vertical plane, the origin of which I do not know.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,patterns.meta,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\foreach \mynormal/\myP in {{(0,0,1)}/{(0,0,h/2)},% normal/point defining plane
	{(1,1,0)}/{(0,0,h/2)},%
	{(1,1,0)}/{(1.5,0,h/2)},%
	{(1,1,2)}/{(0,0,h/2)}}
{\begin{tikzpicture}[declare function={R=2;h=2*R;},same bounding box=A]
 \begin{scope}[3d/install view={phi=0,psi=0,theta=70}]
  \path \myP coordinate (P);
  \pgfmathsetmacro{\myPx}{TD("(P)o(1,0,0)")}
  \pgfmathsetmacro{\myPy}{TD("(P)o(0,1,0)")}
  \pgfmathsetmacro{\myPz}{TD("(P)o(0,0,1)")}
  \pgfmathtruncatemacro{\itest}{sqrt(\myPx*\myPx+\myPy*\myPy)<R?1:0}
  % check that (P) is not outside the cylinder
  \ifnum\itest=0
   \typeout{The point P is not inside the cylinder. Intersection won't be computed.}
  \else
   \path[overlay] \mynormal coordinate (n);
   \pgfmathtruncatemacro{\itest}{TD("(n)o(n)")>0.02?1:0}
   \ifnum\itest=0
	\typeout{Normal is too short. Intersection won't be computed.}
   \else
    \pgfmathsetmacro{\mynn}{TDunit("(n)")}
    \pgfmathsetmacro{\mynx}{TD("(\mynn)o(1,0,0)")}
    \pgfmathsetmacro{\myny}{TD("(\mynn)o(0,1,0)")}
    \pgfmathsetmacro{\mynz}{TD("(\mynn)o(0,0,1)")}
    \pgfmathtruncatemacro{\itest}{(abs(\mynz)>0.01?1:0)}
	\ifcase\itest
	 % normal is in the x-y plane
	 \pgfmathsetmacro{\mys}{screendepth(1,0,0)<0?-1:1}
	 \pgfmathsetmacro{\myex}{TDunit("(0,0,\mys)")}
	 \pgfmathsetmacro{\myey}{TDunit("(\mynn)x(0,0,1)")}
	 \pgfmathtruncatemacro{\mys}{screendepth(\myey)<0?-1:1}
	 \ifnum\mys=-1
	  \pgfmathsetmacro{\myey}{TD("-1*(\myey)")}
	 \fi
	 \pgfmathsetmacro{\mys}{TD("(\mynn)o(\myPx,\myPy,0)")}
	 \pgfmathsetmacro{\myS}{TD("\mys*(\mynn)+(0,0,h/2)")}
	 \path[overlay] (\myex) coordinate (myex) (\myey) coordinate (myey)
   	  (\myS) coordinate (myS);
	 \begin{scope}[x={(myex)},y={(myey)},shift={(myS)}]
      \pgfmathsetmacro{\myr}{sqrt(R*R-\mys*\mys)}
	  \draw[3d/hidden] (h/2,-\myr) -- (-h/2,-\myr) -- (-h/2,\myr);
	  \path[pattern={Lines[angle=-45,distance={2pt}]}] 
	   (-h/2,-\myr) -- (-h/2,\myr) -- (h/2,\myr) -- (h/2,-\myr) -- cycle;
	  \draw[3d/visible] (h/2,-\myr) -- (h/2,\myr) -- (-h/2,\myr);
	 \end{scope}
	\or
	 % normal is generic or in z-direction
	 \tikzset{3d/plane with normal={(\mynn) through (P) named pI},
   	  3d/line through={(0,0,0) and (0,0,h) named lC}}
	 \path[3d/intersection of={lC with pI},overlay] coordinate (myS);	
	 \pgfmathsetmacro{\mynnz}{TD("(\mynn)o(0,0,1)")}
	 \pgfmathsetmacro{\myangle}{acos(\mynnz)}
	 \pgfmathsetmacro{\myangleB}{asin(TD("(\mynn)o(1,0,0)"))}
	 \pgfmathtruncatemacro{\itest}{(abs(\mynz)>0.99?1:0)}
	 \ifnum\itest=0
	  \pgfmathsetmacro{\myey}{TDunit("(n)x(0,0,1)")}
	  \pgfmathsetmacro{\myex}{TDunit("(n)x(\myey)")}
	 \else
	  \pgfmathsetmacro{\myex}{TD("(1,0,0)")}
	  \pgfmathsetmacro{\myey}{TD("(0,1,0)")}
	 \fi 
	 \path[overlay] (\myex) coordinate (myex) (\myey) coordinate (myey);
	 \begin{scope}[x={(myex)},y={(myey)},shift={(myS)}]
	  \draw[3d/hidden]  (\myangleB:{R/cos(\myangle)} and {R})
	   arc[start angle=\myangleB,end angle=\myangleB+180,
	 	  x radius={R/cos(\myangle)},y radius={R}];
	  \path[pattern={Lines[angle=-45,distance={2pt}]}] 
	   circle[x radius={R/cos(\myangle)},y radius={R}];
	  \draw[3d/visible]  (\myangleB:{R/cos(\myangle)} and {R})
	   arc[start angle=\myangleB,end angle=\myangleB-180,
	 	  x radius={R/cos(\myangle)},y radius={R}];
	 \end{scope}
	\fi 
   \fi 
  \fi 
  \pic{3d/frustum={r=R,R=R,h=h}};
 \end{scope}
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=37dae11f6d1b95e09a0668f16605d43fde6161213595db31f0cad708fe0067d9)
comments
transcript

Enter question or answer id or url (and optionally further answer ids/urls from the same question) from

Separate each id/url with a space. No need to list your own answers; they will be imported automatically.