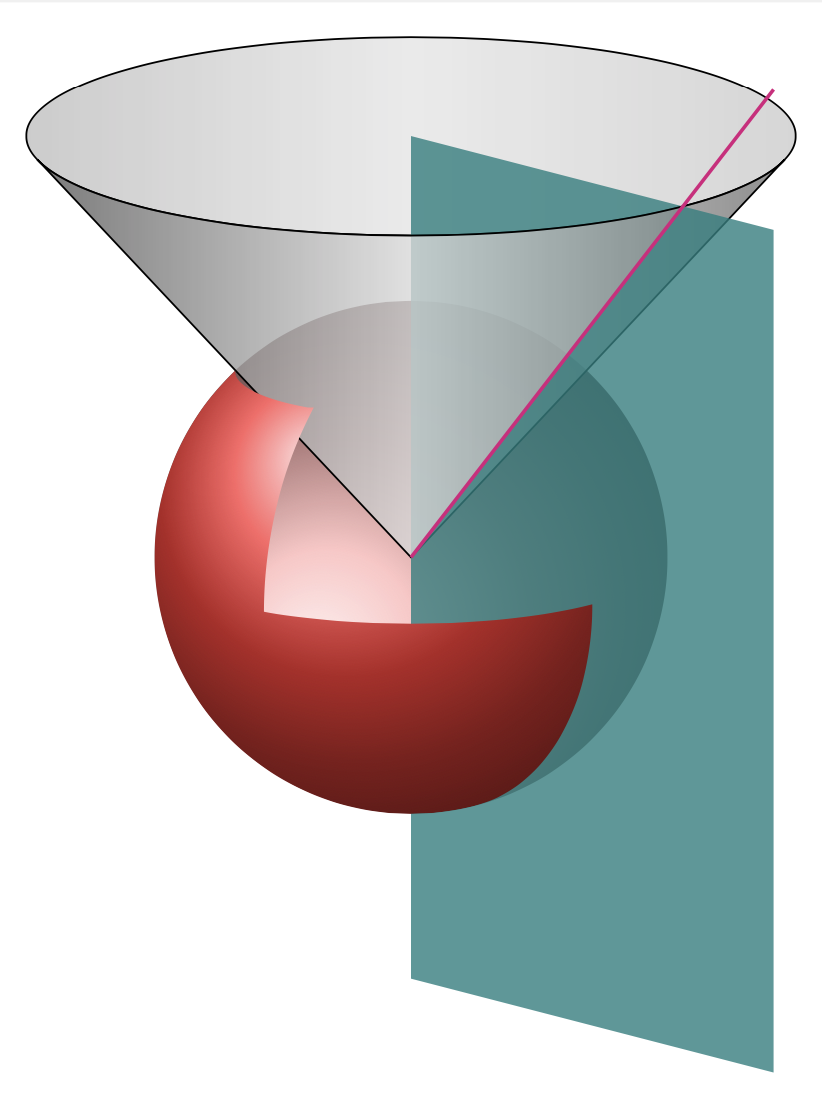
It is possible to draw something that comes somewhat close with Ti*k*Z. However, unless you absolutely need vector graphics, you may be better off with `asymptote` for such pictures.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,decorations.pathreplacing,intersections,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[declare function={R=2;Rp=3;h=1.5;H=4;alpha=80;},
>=stealth]
\path[3d/install view={phi=125-alpha,psi=0,theta=75}]
(1,0,0) coordinate(ex') (0,1,0) coordinate(ey');
\begin{scope}[3d/install view={phi=125,psi=0,theta=75}]
\draw[->] (-3,0,0) -- (3,0,0);
\path (1,0,0) coordinate(ex) (0,1,0) coordinate(ey)
(0,0,1) coordinate(ez) (0,0,h) coordinate (h);
\path[3d/visible/.style={store path=vc},3d/hidden/.style={draw=none}]
pic{3d/circle on sphere={R=R,P={(0,0,0)},n={({-sin(alpha)},{cos(alpha)},0)}}};
\path [stored path/first coordinate of=vc] coordinate (vc-0)
[stored path/last coordinate of=vc] coordinate (vc-1);
% background sphere
\path[3d/screen coords,ball color=red!30,transform canvas={rotate=90},
name path=sphere] (0,0) circle[radius=R];
\pgfmathsetmacro{\r}{sqrt(R*R-h*h)}
\pgfmathsetmacro{\myangle}{asin(h/R)}
\pgfmathsetmacro{\myh}{h*Rp/\r}
% plane inside the cone
\path[fill=teal,opacity=0.8,x={(ex')},canvas is xz plane at y=0] (0,0) -- (0,\myh) --
(Rp,\myh) -- cycle;
% cone
\path[3d/cone/inner/.style={left color=gray!50,right color=gray!40,
middle color=gray!20,on layer=background,fill opacity=0.8},
3d/cone/outer/.style={left color=gray!70!black,right color=gray!90!black,
middle color=gray!30,fill opacity=0.8},
3d/visible/.append style={name path global=cone}]
(0,0,\myh) pic{3d/cone={r=Rp,h=-\myh}};
% complicated sphere segment
\path[name intersections={of=sphere and cone,by={i0,i1}}];
\path[canvas is xy plane at z=h,store path=s1]
let \p1=(i1),\n1={atan2(\y1,\x1)} in
(i1) arc[start angle=\n1,end angle=0,radius=\r];
\path[canvas is xz plane at y=0,store path=s2]
(\myangle:R) arc[start angle=\myangle,end angle=0,radius=R];
\path[canvas is xy plane at z=0,store path=s3]
(0:R) arc[start angle=0,end angle=alpha,radius=R];
\path[x={(ex')},canvas is xz plane at y=0,store path=s4]
let \p1=(vc-0),\n1={atan2(\x1,\y1)} in
(R,0) arc[start angle=0,end angle=90-\n1,radius=R];
\path[3d/screen coords,store path=s5]
let \p1=(vc-0),\n1={atan2(\x1,\y1)},
\p2=(i1),\n2={atan2(\x2,\y2)} in
(90-\n1:R) arc[start angle=90-\n1,end angle=-270-\n2,radius=R];
\path[fill=teal,opacity=0.8,x={(ex')},canvas is xz plane at y=0]
(0,-\myh) -- (0,0) --
(Rp,\myh) -- (H,\myh) -- (H,-\myh) -- cycle;
\draw[x={(ex')},canvas is xz plane at y=0,magenta,thick]
(0,0) -- (4,{4*\myh/Rp});
\begin{scope}
\clip[stored path/restore path=s1,stored path/append path/.list={s2,s3,s4,s5}];
\path[3d/screen coords,ball color=red!80]
(0,0) circle[radius=R];
\end{scope}
\end{scope}
\end{tikzpicture}
\end{document}
```