Draw two right circular cones - TeX

TopAnswers TeX

Meta

Databases

TeX

Code Golf

APL

C++

.net

db<>fiddle

Java

*nix

PHP

PowerShell

Python

Rust

टेक्-मराठी

Typst

Web Client Dev

Web Server Dev

Draw two right circular cones

tikz add tag

Anonymous 1123

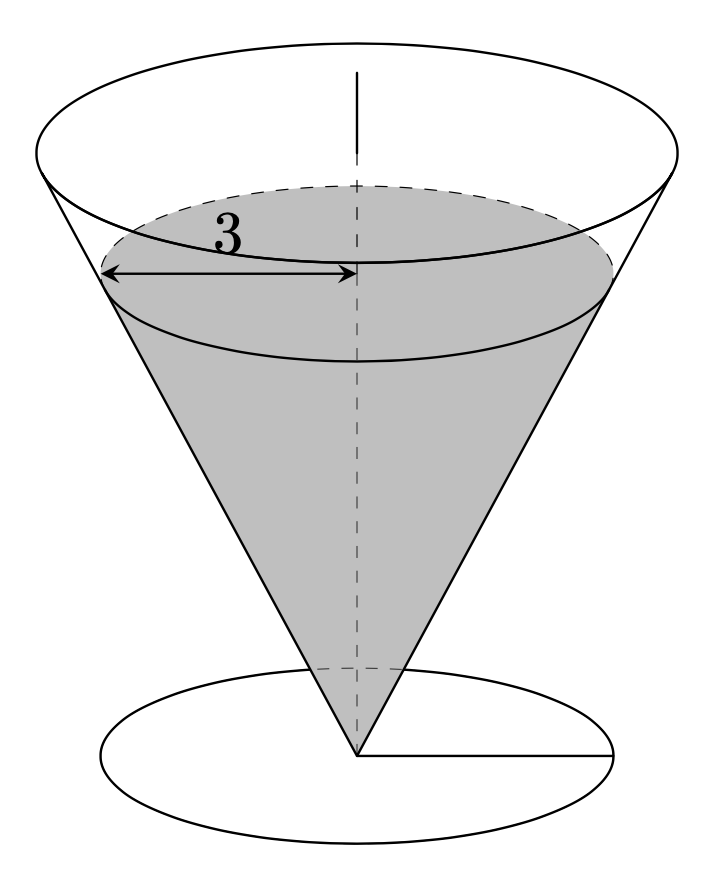
I copied this code from [here](https://artofproblemsolving.com/wiki/index.php?title=2021_AMC_12A_Problems&action=edit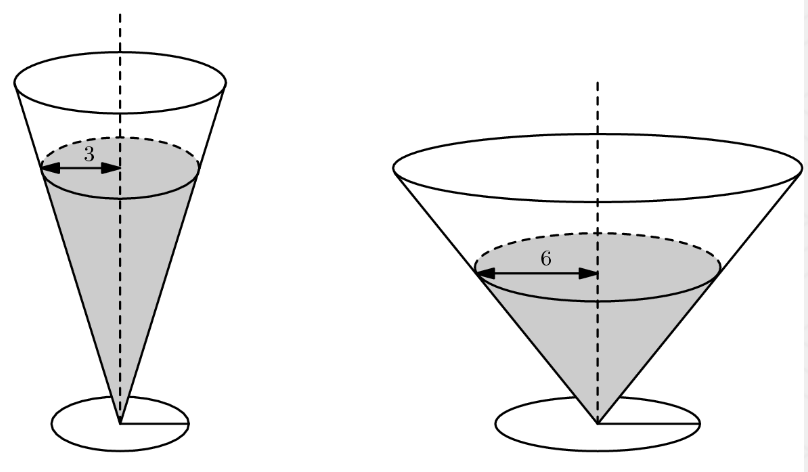&section=10) ![image.png](/image?hash=b4be8cc37dce5dd0da07c2dce11b088c16440c26f7ff59a8e7bb5d5077f1e62e)
```
size(350);
defaultpen(linewidth(0.8));
real h1 = 10, r = 3.1, s=0.75;
pair P = (r,h1), Q = (-r,h1), Pp = s * P, Qp = s * Q;
path e = ellipse((0,h1),r,0.9), ep = ellipse((0,h1*s),r*s,0.9);
draw(ellipse(origin,r*(s-0.1),0.8));
fill(ep,gray(0.8));
fill(origin--Pp--Qp--cycle,gray(0.8));
draw((-r,h1)--(0,0)--(r,h1)^^e);
draw(subpath(ep,0,reltime(ep,0.5)),linetype("4 4"));
draw(subpath(ep,reltime(ep,0.5),reltime(ep,1)));
draw(Qp--(0,Qp.y),Arrows(size=8));
draw(origin--(0,12),linetype("4 4"));
draw(origin--(r*(s-0.1),0));
label("$3$",(-0.9,h1*s),N,fontsize(10));

real h2 = 7.5, r = 6, s=0.6, d = 14;
pair P = (d+r-0.05,h2-0.15), Q = (d-r+0.05,h2-0.15), Pp = s * P + (1-s)*(d,0), Qp = s * Q + (1-s)*(d,0);
path e = ellipse((d,h2),r,1), ep = ellipse((d,h2*s+0.09),r*s,1);
draw(ellipse((d,0),r*(s-0.1),0.8));
fill(ep,gray(0.8));
fill((d,0)--Pp--Qp--cycle,gray(0.8));
draw(P--(d,0)--Q^^e);
draw(subpath(ep,0,reltime(ep,0.5)),linetype("4 4"));
draw(subpath(ep,reltime(ep,0.5),reltime(ep,1)));
draw(Qp--(d,Qp.y),Arrows(size=8));
draw((d,0)--(d,10),linetype("4 4"));
draw((d,0)--(d+r*(s-0.1),0));
label("$6$",(d-r/4,h2*s-0.06),N,fontsize(10));
```
How to draw this code with `3dtools`?

This is some options are drawn with GeospacW
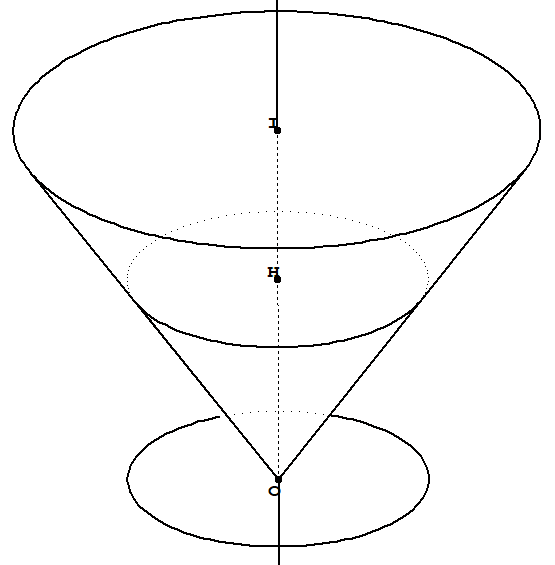
![ScreenHunter 12.png](/image?hash=99d87a5d268585add499616a6094cfcbdb1c98f4e7129f79aca062ca36e7085b)

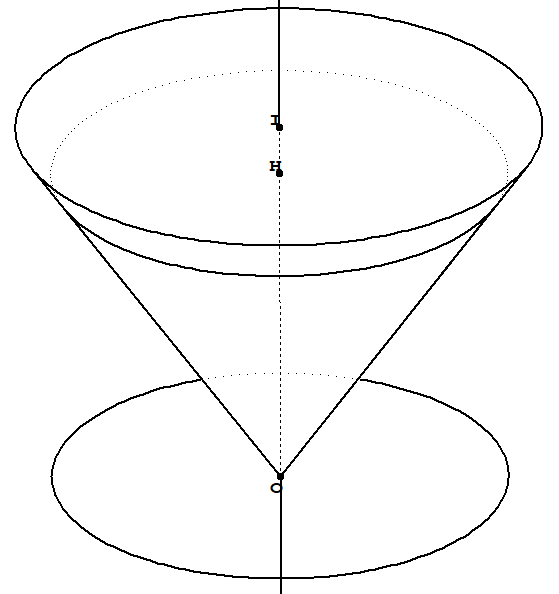
![ScreenHunter 13.png](/image?hash=5a076682b7be14fa354bd7137c1df2db79d1d135066bf8e9f9dd2bbb5d0b5cb7)

Top Answer

user 3.14159

Here are some ways to draw such figures. On cannot use the built-in cone for everything since the visibility of the inner cone is determined by the outer cone.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,3dtools}%https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground} 
\begin{tikzpicture}[3d/install view={phi=0,theta=70},
	scale=0.5,transform shape,
	line cap=round,line join=round,
	declare function={R=3;H=6;a=1.25;Hprime=(a-1)*H;}]
	\path pic[3d/visible/.style={fill=gray,fill opacity=0.5}]{3d/cone={r=R,h=-H}}
	 (0,0,Hprime) pic[3d/visible/.append style={save named path=C}]{3d/cone={r=a*R,h=-a*H}};
	\draw (0,0,-H) -- (R,0,-H);  
	\path[save named path=B] (0,0,-H) circle[radius=R]; 
	\begin{scope}
	 \clip[even odd clip,use named path=C,generous outside path]; 
	 \draw[3d/visible,use named path=B];
	\end{scope} 
	\begin{scope}
	 \clip[use named path=C]; 
	 \draw[3d/hidden,on layer=background,use named path=B];
	\end{scope} 
	\pgfmathsetmacro{\sdtip}{screendepth(0,0,H)}
	\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(H*H-\sdtip*\sdtip))}
	\draw[3d/visible] (0,0,Hprime) -- ++ (0,0,1);
	\draw[3d/hidden] (0,0,Hprime) -- (0,0,0);
	\draw[3d/hidden,on layer=background] (0,0,0) -- (0,0,-H);
	\pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*R/H)<1}
	\ifnum\itest=1
	 \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*R/H)}
     \begin{scope}[canvas is xy plane at z=0]
	  \draw[3d/hidden] (\alphacrit-90:R)
		 arc[start angle=\alphacrit-90,end angle=270-\alphacrit,radius=R];  
	  \draw[3d/visible] (\alphacrit-90:R)
		 arc[start angle=\alphacrit-90,end angle=-90-\alphacrit,radius=R];  
	  \draw[stealth-stealth] (0,0) -- node[above,transform shape=false]
	   {$\pgfmathparse{R}\pgfmathprintnumber\pgfmathresult$}(-R,0);	
	 \end{scope}	
    \fi
\end{tikzpicture}
\end{document}
```
![Screen Shot 2021-02-27 at 8.15.49 PM.png](/image?hash=e0b350c8581cfd5b86cdab42f1ccf7e07cd13e741050e8b8f0237c48e207e4ab)

1 Answer