There are many possibilities. One of them is `pgfplots`. A possible parametrization of tori is stored in [`3dtools`](https://github.com/marmotghost/tikz-3dtools), which we just load and use here.

```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\usepackage{pgfplots}
\pgfplotsset{compat=1.17}
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,miter limit=5]
 \begin{axis}[width=15cm,unit vector ratio=1 1 1,
 	view={120}{30},hide axis,declare function={R=1;r=1;d=1;},
 	xmin=-R-r-d,ymin=-R-r-d,zmin=-r-d,
    xmax=R+r+d,ymax=R+r+d,zmax=r+d,
		]
  \addplot3[surf,fill=white,
   colormap/blackwhite,point meta=0,
   z buffer=sort,
   samples=36,samples y=36,
   domain=0:360,y domain=0:360]
   ({torusx(x,y,R,r)},{torusy(x,y,R,r)},{torusz(x,y,R,r)}); 
  \pgfmathsetmacro{\myu}{\pgfkeysvalueof{/pgfplots/view/az}-90} 
  \pgfmathsetmacro{\myv}{90+\pgfkeysvalueof{/pgfplots/view/el}}
  \typeout{\myu,\myv}
  \draw[-stealth] (R+r,0,0) -- (R+r+d,0,0) node[below]{$x$};
  \draw[-stealth] (0,R+r,0) -- (0,R+r+d,0) node[below]{$y$};
  \draw[-stealth] ({torusx(\myu,\myv,R,r)},{torusy(\myu,\myv,R,r)},{torusz(\myu,\myv,R,r)})
  	-- (0,0,R+d,0) node[above]{$z$};
 \end{axis}
\end{tikzpicture}
\end{document}
```
![Screen Shot 2021-02-12 at 10.43.00 AM.png](/image?hash=36838b1a478d30afe455bf89cf82fd11f796ebdc75cfe12042fd8b7cc6b188ec)

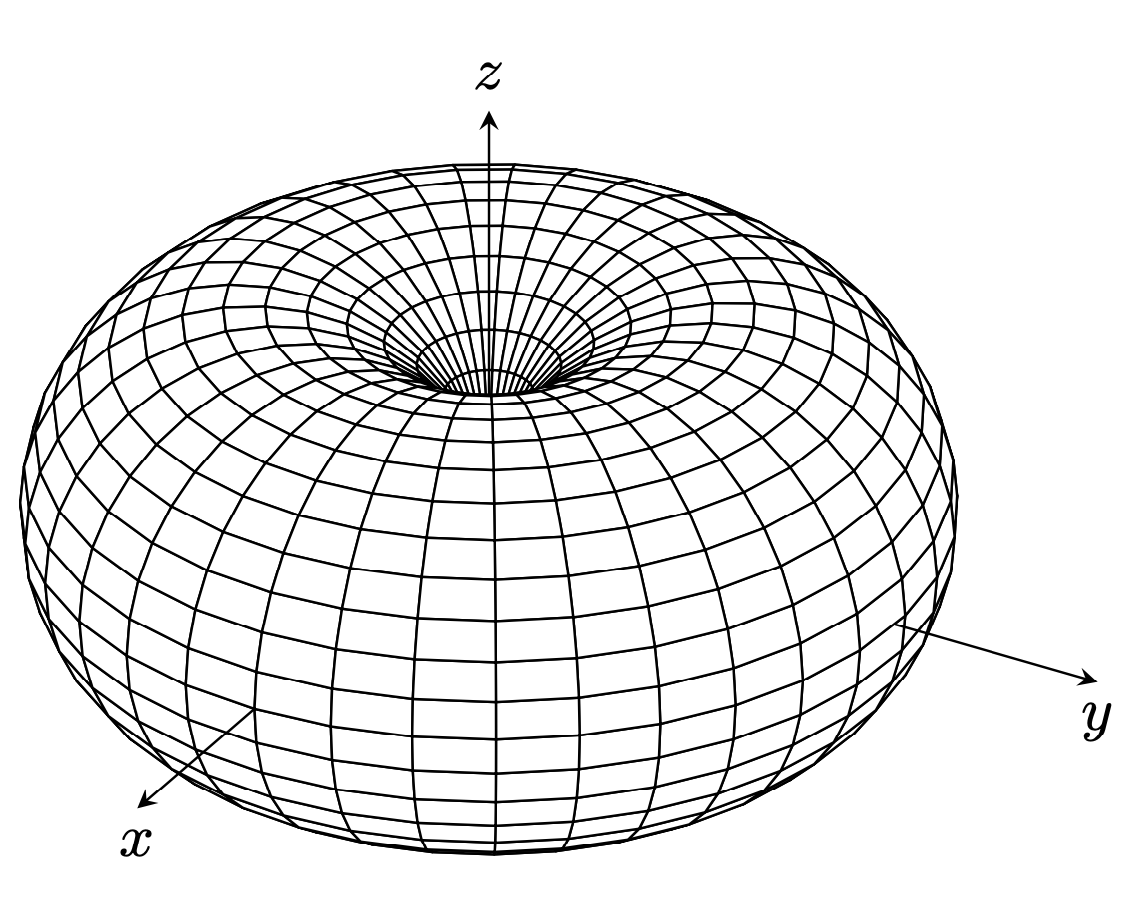
As usual, there are pros and cons. The pro is that this is vector graphics and Ti*k*Z-based, so ond does not have to learn a completely new syntax, and can familiar concepts and styles. The downside is that this is just and orthographic projection, no fully realistic view, nor shading. If you want the latter, consider using `asymptote`, which will, however, lead to pixel graphics. You *can* [produce vector graphics with `asymptote`](https://tex.stackexchange.com/a/151170), however, this amounts to determining the visibility on your own. That is, you have to employ a similar strategy to what you know from the various `3dtools` pics (but of course the asymptote torus code by Charles Staats predates `3dtools`, and so do many others).