Anonymous 1123

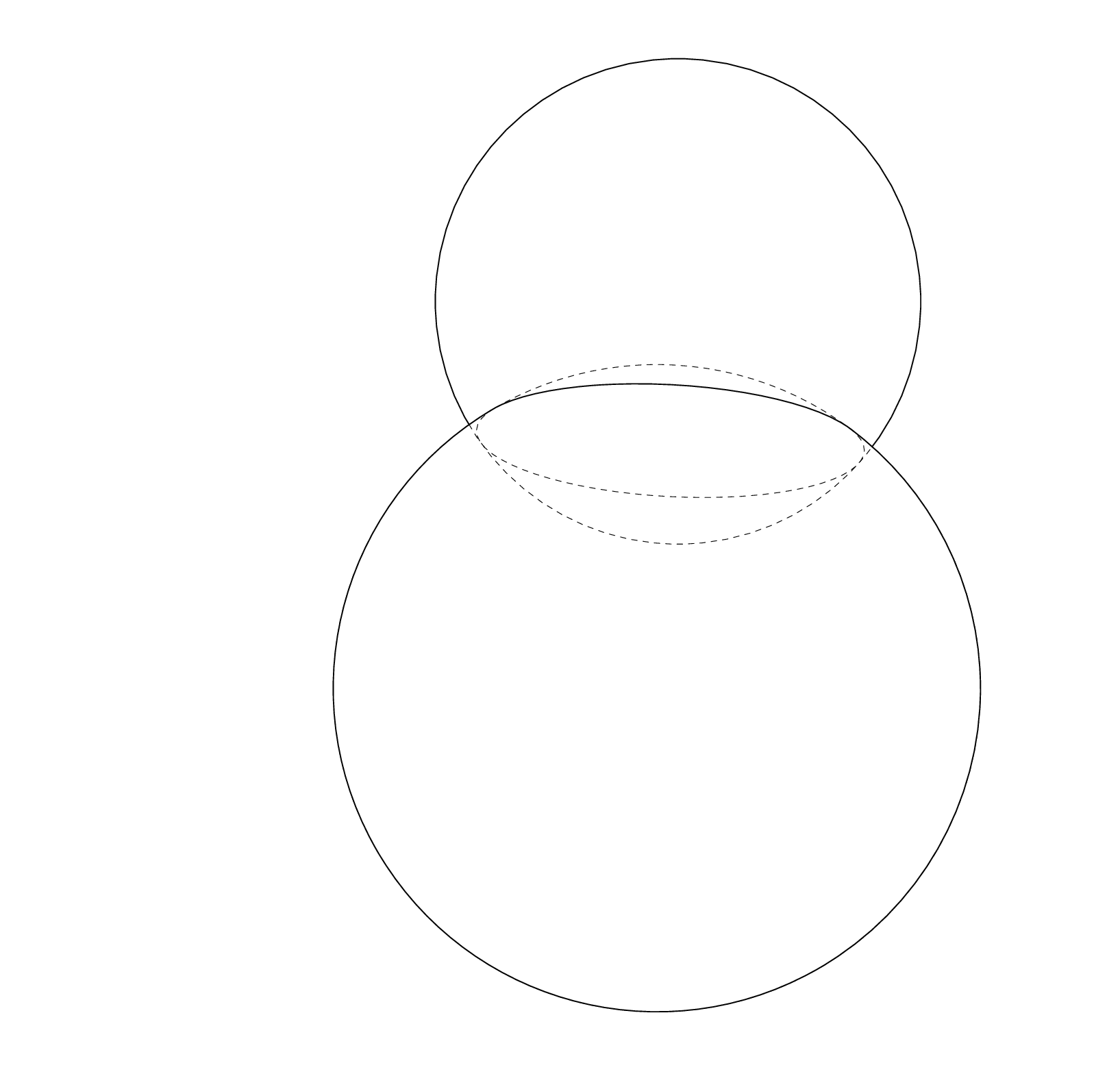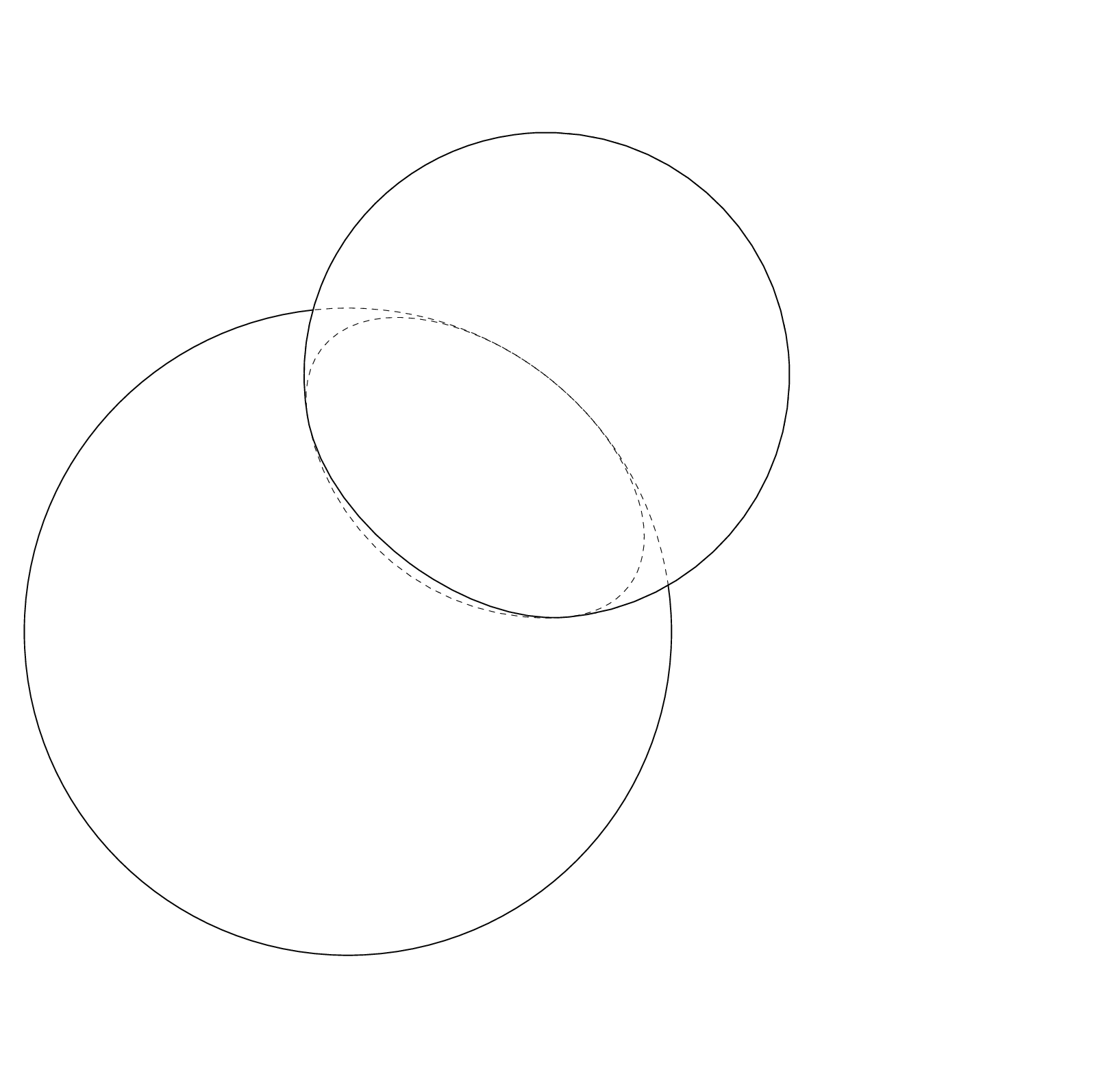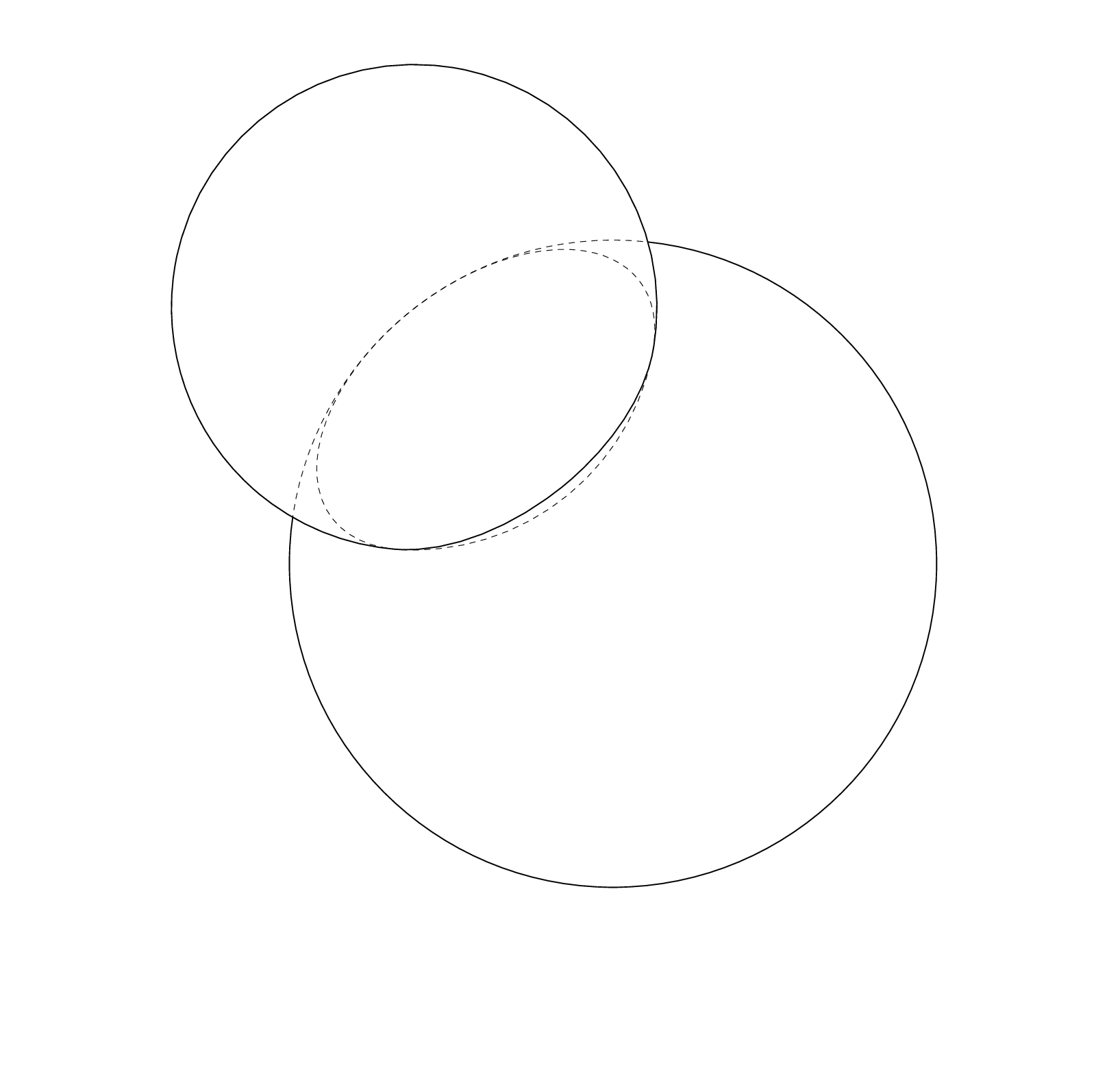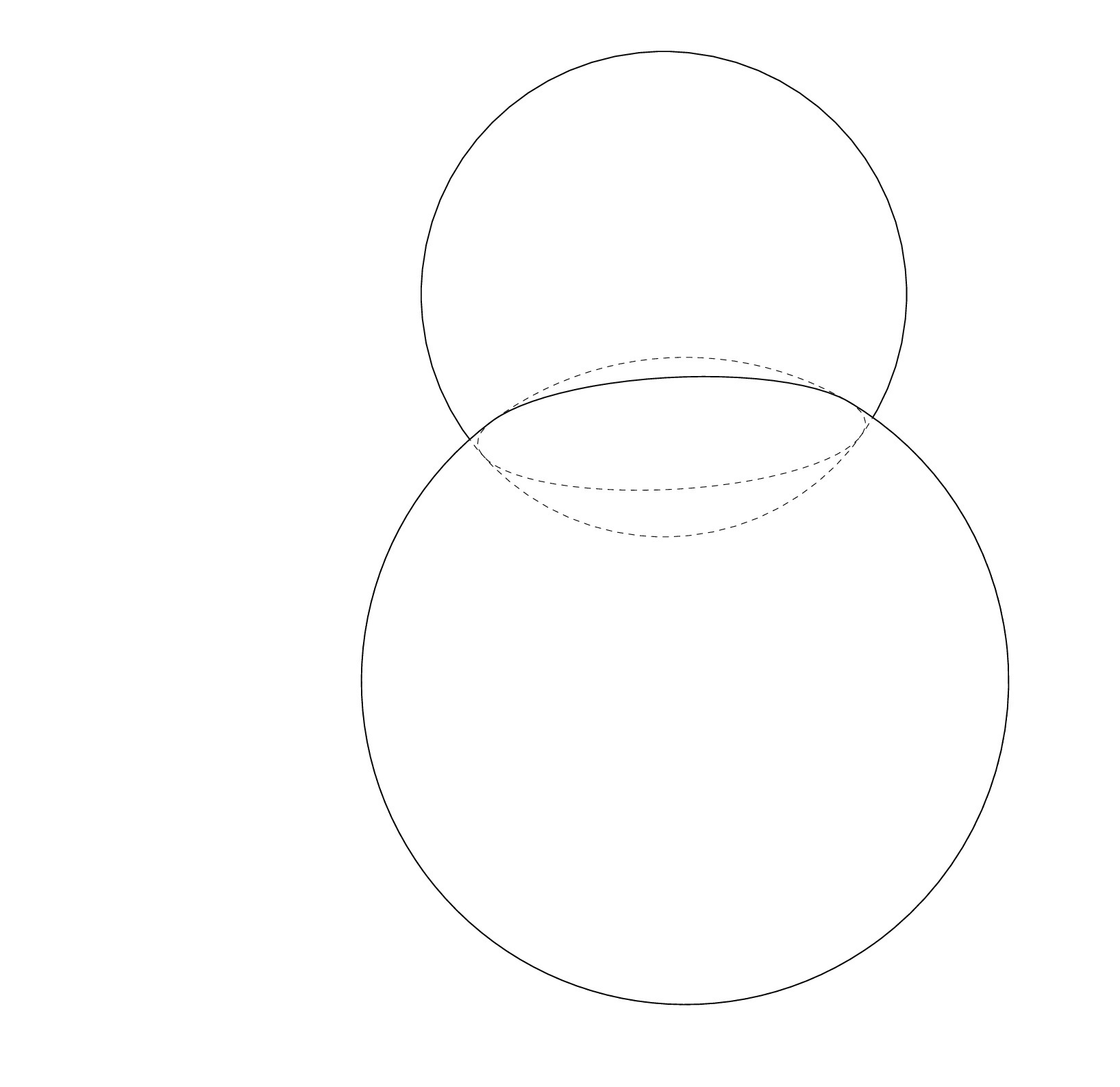
Based on a question [here](https://tex.stackexchange.com/questions/518502/circle-made-from-intersecting-spheres/518749#518749), I have two spheres with equations `(x - 3)^2 + (y + 4)^2 + z^2 = 64` and `(x - 3)^2 + (y - 2)^2 + (z - 8)^2 = 36`.
I tried
```
\documentclass[tikz,border=2mm, 12 pt]{standalone}
\usepackage{tikz-3dplot-circleofsphere}
\usetikzlibrary{3dtools}
\begin{document}
\tdplotsetmaincoords{70}{100}
\begin{tikzpicture}[scale=1,tdplot_main_coords,declare function={R=8;R1=6;
}]
\path (3,-4,8) coordinate (A)
({(9-sqrt(95))/3},8/3,3) coordinate (B)
({(9+sqrt(95))/3},8/3,3) coordinate (C)
(3,2,8) coordinate (T)
(3,-4,0) coordinate (I);
\begin{scope}[tdplot_screen_coords]
\fill[ball color=red,opacity=0.6] (I) circle (R);
\fill[ball color=green!50, opacity=1.0] (T) circle (R1);
\end{scope}
\foreach \p in {A,B,C,I,T}
\draw[fill=black] (\p) circle (1.5pt);
\foreach \p/\g in {A/90,C/-90,B/-90,I/-90,T/90}
\path (\p)+(\g:3mm) node{$\p$};
\pic[draw=none]{3d circle through 3 points={A={(A)},B={(B)},C={(C)}}};
\begin{scope}[shift={(T)}]
\path[overlay] [3d coordinate={(myn)=(A)-(B)x(A)-(C)},
3d coordinate={(A-M)=(A)-(M)}];
\pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")}
\pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]}
\pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]}
\pgfmathsetmacro{\mygamma}{acos(sqrt(TD("(A-M)o(A-M)"))/R1)}
\tdplotCsDrawCircle[tdplotCsFront/.style={thick,red}]{R1}{\myalpha}{\mybeta}{\mygamma}
\end{scope}
\end{tikzpicture}
\end{document}
```
How to draw intersection of two spheres like this
Top Answer
user 3.14159

This uses the `circle on sphere` pic with some path management to produce the hopefully correct clips. Some annotations are added to provide additional information.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,decorations.pathreplacing,3dtools} % https://github.com/marmotghost/tikz-3dtools
\begin{document}
\foreach \Angle in {5,15,...,355}
{\begin{tikzpicture}[line cap=round,line join=round,
same bounding box=A,
3d/install view={phi=\Angle,theta=70},
declare function={r1=4;r2=3;}]
\path (1.5,-2,0) coordinate (A)
(1.5,1,4) coordinate (B);
\pgfmathsetmacro{\d}{sqrt(TD("(A)-(B)o(A)-(B)"))}
\pgfmathsetmacro{\myd}{(\d*\d+r1*r1-r2*r2)/2/\d}
\pgfmathsetmacro{\myr}{sqrt(r1*r1-\myd*\myd)}
\pgfmathsetmacro{\mym}{TDunit("(B)-(A)")}
\pgfmathsetmacro{\mym}{TD("(A)+\myd*(\mym)")}
\path (\mym) coordinate (m);
\pgfmathtruncatemacro{\itest}{(TD("(A)-(B)o(nscreenx,nscreeny,nscreenz)")<0?0:1)}
% to avoid duplication, call the center of the sphere in the foreground \myA with
% radius \myR, and the other center \myB with radius \myRp
\ifnum\itest=1
\edef\myA{A}
\edef\myB{B}
\pgfmathsetmacro{\myR}{r1}
\pgfmathsetmacro{\myRp}{r2}
\else
\edef\myA{B}
\edef\myB{A}
\pgfmathsetmacro{\myR}{r2}
\pgfmathsetmacro{\myRp}{r1}
\fi
% just to get the bounding box right
\path[3d/screen coords] (A) circle[radius=r1] (B) circle[radius=r2];
\path[stored path/reset coordinate index,
3d/visible/.style={store path=tmp}]
pic{3d/circle on sphere={R=\myR,P={(m)},C={(\myA)}}};
% check if there is a visible stretch (if yes, \np>0)
\pgfmathtruncatemacro{\np}{tikztdindexoflastcoordinate}
\ifnum\np>0
\path [stored path/first coordinate of=tmp] coordinate (tmp-first)
[stored path/last coordinate of=tmp] coordinate (tmp-last);
\draw[3d/screen coords,3d/visible,postaction={store path=fore}]
let \p1=($(tmp-first)-(\myA)$),\p2=($(tmp-last)-(\myA)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)},
\n3={(abs(\n1-\n2)<180?\n1+360:\n1)} in
[stored path/restore path=tmp] -- (tmp-last)
arc[start angle=\n2,end angle=\n3,radius=\myR] -- cycle;
\begin{scope}[3d/screen coords]
\begin{scope}
\clip[overlay,stored path/restore path=fore];
\draw[3d/hidden] (\myB) circle[radius=\myRp];
\end{scope}
\begin{scope}
\clip[overlay,even odd clip,stored path/restore path=fore,generous outside path];
\draw[3d/hidden] (\myA) circle[radius=\myR];
\draw[3d/visible] (\myB) circle[radius=\myRp];
\end{scope}
\end{scope}
\else
\begin{scope}[3d/screen coords]
\begin{scope}
\draw[3d/visible] (\myA) circle[radius=\myR];
\clip (\myA) circle[radius=\myR];
\draw[3d/hidden] (\myB) circle[radius=\myRp];
\end{scope}
\begin{scope}
\clip[overlay,even odd clip] (\myA) circle[radius=\myR] [generous outside path];
\draw[3d/visible] (\myB) circle[radius=\myRp];
\end{scope}
\end{scope}
\fi
\end{tikzpicture}}
\end{document}
```