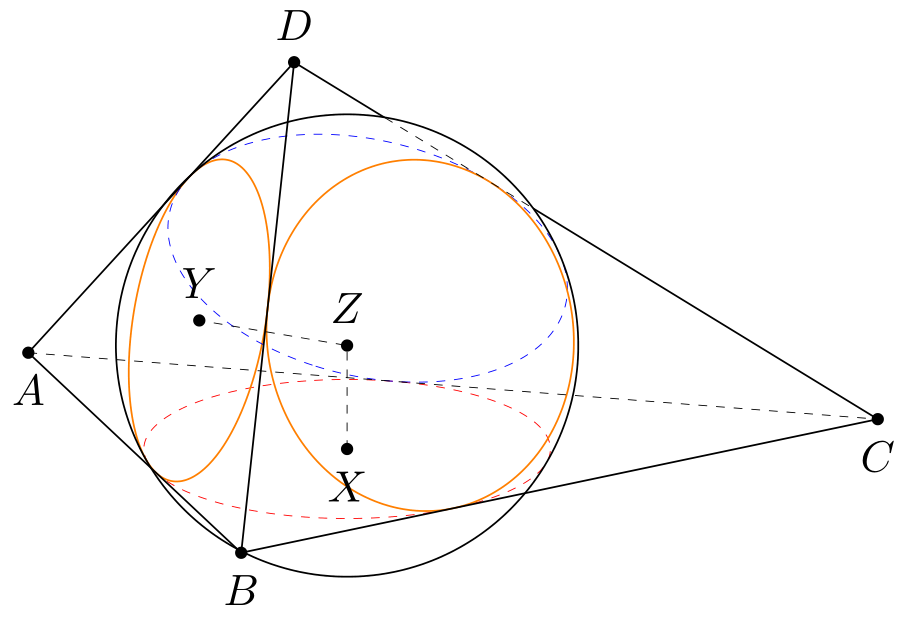
I am trying to draw sphere is tangent with every edge of a tetrahedron. I know that such a sphere exists if and only if one of the following conditions is met:
1. the sums of the lengths of pairs of opposite edges are equal;
2. the circles inscribed in the faces touch in pairs;
3. the perpendiculars to the planes of the faces, raised from the centers of the circles inscribed in the faces, intersect at one point.
By using *Maple*, I consider a tetrahedron ABCD for which the edge lengths are known: `AB=5, BC=6, AC=7, AD=5, BD=4, CD = 6`. *Maple* give center of sphere is `I(3,1.632993162,.8845536331)` and radius `R=1.857175758`
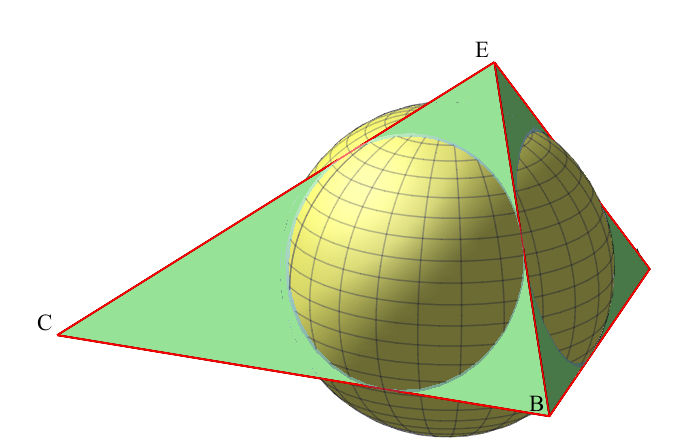
I tried
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,
line join=round,visible/.style={draw,solid},
hidden/.style={draw,very thin,cheating dash},declare function={R=1.857175758;}]
\path
(0,0,0) coordinate (A)
(19/7,{12*sqrt(6)/7},0) coordinate (B)
(7, 0,0) coordinate (C)
(19/7, {59*sqrt(6)/63},{sqrt(1002)/9}) coordinate (D)
(3,1.632993162,.8845536331) coordinate (I)
;
\shade[ball color=white,3d/screen coords] (I) circle[radius=R];
\path pic[red,hidden]{3d incircle={%
A={(A)},B={(B)},C={(C)}}};
\path pic[blue,hidden]{3d incircle={%
A={(A)},B={(B)},C={(D)}}};
\path pic[orange,visible]{3d incircle={%
A={(A)},B={(D)},C={(C)}}};
\path pic[orange,visible]{3d incircle={%
A={(D)},B={(B)},C={(C)}}};
\foreach \p in {A,B,C,D}
{\draw[fill=black] (\p) circle (1.2 pt);}
\foreach \p/\g in {A/-90,B/-90,C/-90,D/90,I/90}
{\path (\p)+(\g:3mm) node{$\p$};}
\draw[hidden]
(A) -- (B) ;
\draw [visible] (D) -- (A) -- (C) -- (B) -- cycle (D) -- (C);
\end{tikzpicture}
\end{document}
```
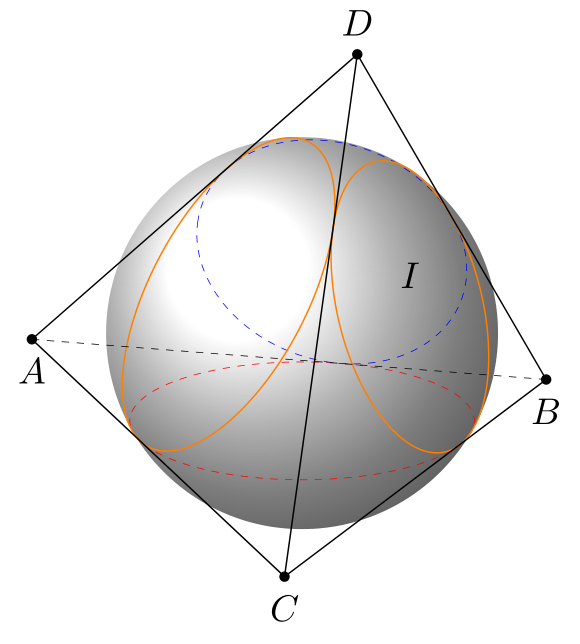
I know that, the sphere knowing six edgs at [here](https://topanswers.xyz/tex?q=1349)
How to draw a sphere is tangent with every edge of a tetrahedron without using Maple?
**PS.** The option of the point `I` seems incorrect.
**ACTUALLY FOR A REGULAR TETRAHEDRON.**
Let given a tetrahedron has coordinates of the center `O(0,0,0)`, radius of the sphere is `R=a`, coordinates of the vertices is ` (a,a,a), (a,-a,-a), (-a,a,-a), (-a,-a,a)`
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,
line join=round,visible/.style={draw,solid},
hidden/.style={draw,very thin,cheating dash},declare function={R=3;a=R;}]
\path
(a,a,a) coordinate (A)
(a,-a,-a) coordinate (B)
(-a,a,-a) coordinate (C)
(-a,-a,a) coordinate (D)
(0,0,0) coordinate (I)
;
\shade[ball color=white,3d/screen coords] (I) circle[radius=R];
\path pic[red,hidden]{3d incircle={%
A={(A)},B={(B)},C={(C)}}};
\path pic[blue,hidden]{3d incircle={%
A={(A)},B={(B)},C={(D)}}};
\path pic[orange,visible]{3d incircle={%
A={(A)},B={(D)},C={(C)}}};
\path pic[orange,visible]{3d incircle={%
A={(D)},B={(B)},C={(C)}}};
\foreach \p in {A,B,C,D}
{\draw[fill=black] (\p) circle (1.2 pt);}
\foreach \p/\g in {A/-90,B/-90,C/-90,D/90}
{\path (\p)+(\g:3mm) node{$\p$};}
\draw[hidden]
(A) -- (B) ;
\draw [visible] (D) -- (A) -- (C) -- (B) -- cycle (D) -- (C);
\end{tikzpicture}
\end{document}
```
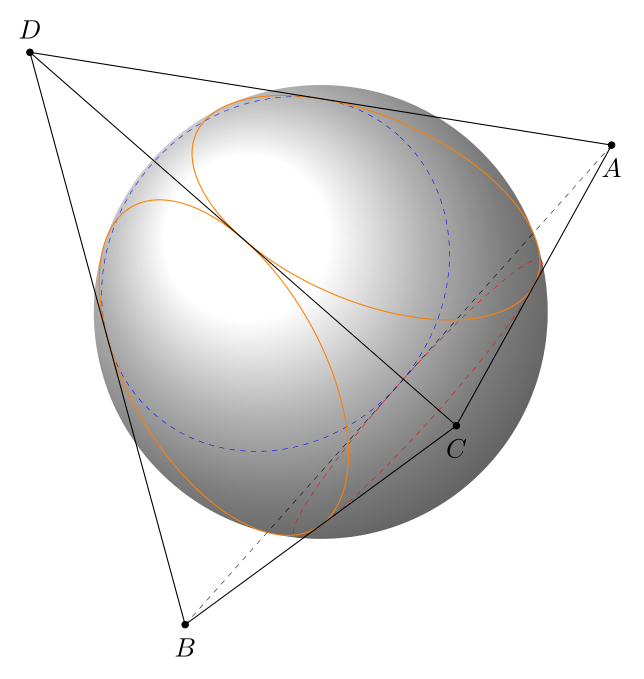
About the point `I`, if I rename `I` by `T`, I get correct result.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,
line join=round,visible/.style={draw,solid},
hidden/.style={draw,very thin,cheating dash},declare function={R=1.857175758;}]
\path
(0,0,0) coordinate (A)
(19/7,{12*sqrt(6)/7},0) coordinate (B)
(7, 0,0) coordinate (C)
(19/7, {59*sqrt(6)/63},{sqrt(1002)/9}) coordinate (D)
(3,1.632993162,.8845536331) coordinate (T)
;
\shade[ball color=white,3d/screen coords] (T) circle[radius=R];
\path pic[red,hidden]{3d incircle={%
A={(A)},B={(B)},C={(C)}}};
\path pic[blue,hidden]{3d incircle={%
A={(A)},B={(B)},C={(D)}}};
\path pic[orange,visible]{3d incircle={%
A={(A)},B={(D)},C={(C)}}};
\path pic[orange,visible]{3d incircle={%
A={(D)},B={(B)},C={(C)}}};
\foreach \p in {A,B,C,D,T}
{\draw[fill=black] (\p) circle (1.2 pt);}
\foreach \p/\g in {A/-90,B/-90,C/-90,D/90,T/90}
{\path (\p)+(\g:3mm) node{$\p$};}
\draw[hidden]
(A) -- (B) ;
\draw [visible] (D) -- (A) -- (C) -- (B) -- cycle (D) -- (C);
\end{tikzpicture}
\end{document}
```
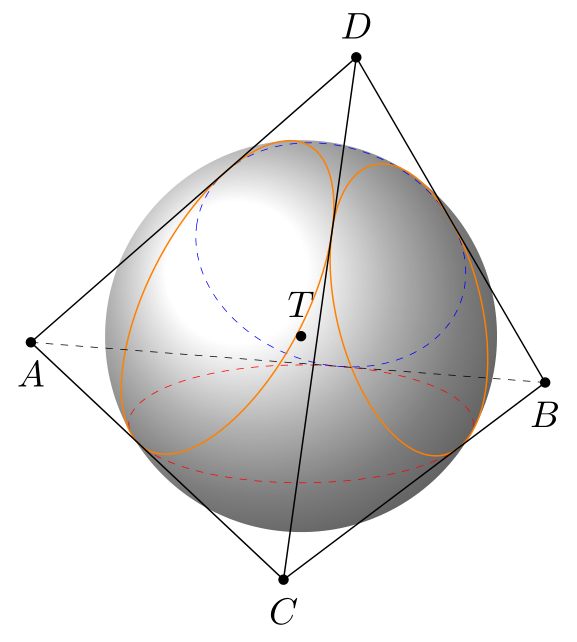Here is a first version. The tetrahedron is constructed similarly to [the post you link to](https://topanswers.xyz/tex?q=1349) but now more constructions have been added to the [`3dtools` library](https://github.com/marmotghost/tikz-3dtools) so this is easier. Then we can construct the incircles of each face, and in the construction of these the touching points are automatically determined. We can then construct the sphere by taking four touching points that do not lie in a plane (which requires a bit trial and error). The intersection of the sphere with the faces can then be drawn with the `3d/circle on sphere` key.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[line cap=round,line join=round,
dot/.style={circle,inner sep=1pt,fill},
declare function={lAB=5;lAC=7;lBC=6;lAD=5;lBD=4;lCD=6;}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=70,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos(-1*(lBC*lBC-lAC*lAC-lAB*lAB)/(2*lAB*lAC))}
\path (0,0,0) coordinate (A)
(lAB,0,0) coordinate (B)
({lAC*cos(\mytheta)},{lAC*sin(\mytheta)},0) coordinate (C);
% cross checks
% \pgfmathsetmacro{\dAB}{tddistance("(A)","(B)")}%
% \pgfmathsetmacro{\dAC}{tddistance("(A)","(C)")}%
% \pgfmathsetmacro{\dBC}{tddistance("(B)","(C)")}%
% \typeout{\dAB,\dBC,\dAC}
\path[overlay,3d/aux keys/i1=D,3d/aux keys/i2=D',
3d/intersection of three spheres={rA=lAD,rB=lBD,rC=lCD}];
\path[pic actions/.append style={draw=none}]
foreach \X/\Y/\Z in {A/B/C,A/B/D,A/C/D,B/C/D}
{pic{3d incircle={A={(\X)},B={(\Y)},C={(\Z)},
center name=i\X\Y\Z,projection prefix=in\X\Y\Z}}};
\path[3d/circumsphere center={A={(inABCb)},B={(inABDc)},C={(inACDb)},D={(inBCDa)}}]
coordinate (I) (I) node[dot,label=above:{$I$}]{} ;
\pgfmathsetmacro{\myR}{tddistance("(I)","(inABCb)")}% radius of sphere
\draw[3d/screen coords] (I) circle[radius=\myR];
\path[overlay,3d coordinate={(O')=0.25*(A)+0.25*(B)+0.25*(C)+0.05*(D)}];
\tikzset{3d/polyhedron/.cd,O={(O')},
fore layer=foreground,back layer=background,
fore/.append style={fill opacity=0.4,thick}, back/.append style={fill opacity=0.4},
draw face with corners={{(A)},{(B)},{(C)}},
draw face with corners={{(A)},{(B)},{(D)}},
draw face with corners={{(A)},{(C)},{(D)}},
draw face with corners={{(B)},{(C)},{(D)}}}
\foreach \X/\Y/\Z in {A/B/C,A/B/D,A/C/D,B/C/D}
{\path pic{3d/circle on sphere={C={(I)},R=\myR,P={(i\X\Y\Z)}}};}
\end{scope}
\end{tikzpicture}
\end{document}
```
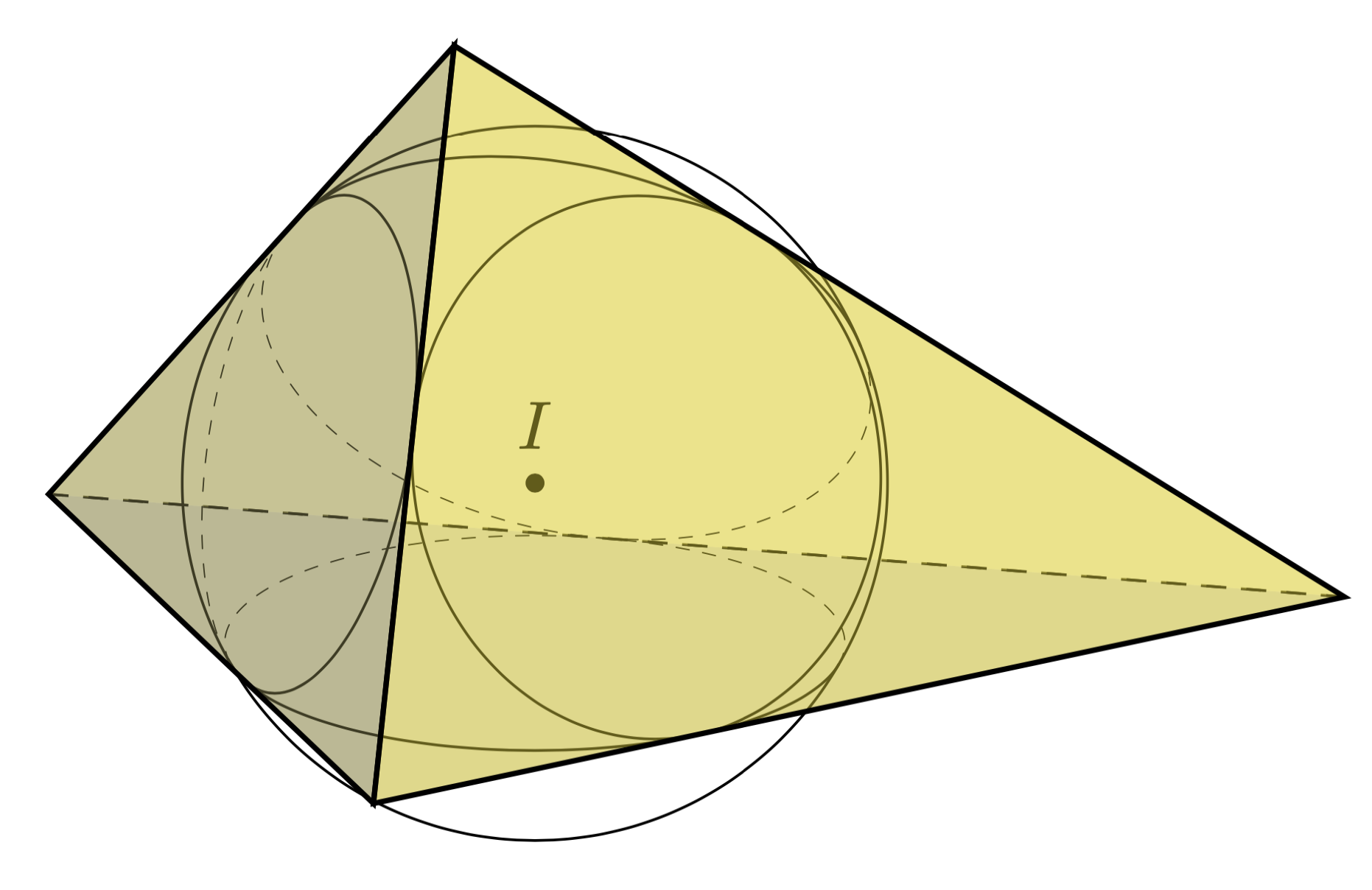
A version that has no colored faces and distinguishes between hidden and visibe stretches:
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc,decorations.pathreplacing,3dtools} % https://github.com/marmotghost/tikz-3dtools
\begin{document}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{tikzpicture}[line cap=round,line join=round,
dot/.style={circle,inner sep=1pt,fill},
declare function={lAB=5;lAC=7;lBC=6;lAD=5;lBD=4;lCD=6;}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=70,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos(-1*(lBC*lBC-lAC*lAC-lAB*lAB)/(2*lAB*lAC))}
\path (0,0,0) coordinate (A)
(lAB,0,0) coordinate (B)
({lAC*cos(\mytheta)},{lAC*sin(\mytheta)},0) coordinate (C);
% cross checks
% \pgfmathsetmacro{\dAB}{tddistance("(A)","(B)")}%
% \pgfmathsetmacro{\dAC}{tddistance("(A)","(C)")}%
% \pgfmathsetmacro{\dBC}{tddistance("(B)","(C)")}%
% \typeout{\dAB,\dBC,\dAC}
\path[overlay,3d/aux keys/i1=D,3d/aux keys/i2=D',
3d/intersection of three spheres={rA=lAD,rB=lBD,rC=lCD}];
\path[pic actions/.append style={draw=none}]
foreach \X/\Y/\Z in {A/B/C,A/B/D,A/C/D,B/C/D}
{pic{3d incircle={A={(\X)},B={(\Y)},C={(\Z)},
center name=i\X\Y\Z,projection prefix=in\X\Y\Z}}};
\path[3d/circumsphere center={A={(inABCb)},B={(inABDc)},C={(inACDb)},D={(inBCDa)}}]
coordinate (I) (I) node[dot,label=above:{$I$}]{} ;
\pgfmathsetmacro{\myR}{tddistance("(I)","(inABCb)")}% radius of sphere
\begin{scope}
\clip[overlay,convex hull of={A,B,C,D},generous outside path'];
\draw[3d/screen coords,3d/visible] (I) circle[radius=\myR];
\end{scope}
\begin{scope}
\clip[overlay,convex hull of={A,B,C,D}];
\draw[3d/screen coords,3d/hidden] (I) circle[radius=\myR];
\end{scope}
\path[overlay,3d coordinate={(O')=0.25*(A)+0.25*(B)+0.25*(C)+0.05*(D)}];
\tikzset{3d/polyhedron/.cd,O={(O')},
fore layer=foreground,back layer=background,
fore/.append style={fill opacity=0,thick}, back/.append style={fill opacity=0},
draw face with corners={{(A)},{(B)},{(C)}},
draw face with corners={{(A)},{(B)},{(D)}},
draw face with corners={{(A)},{(C)},{(D)}},
draw face with corners={{(B)},{(C)},{(D)}}}
\foreach \X/\Y/\Z in {A/B/C,A/B/D,A/C/D,B/C/D}
{\pgfmathsetmacro{\itest}{TD("(nscreenx,nscreeny,nscreenz)o(i\X\Y\Z)-(I)")>0?1:0}
\ifnum\itest=1
\path[%3d/visible/.append style={store path=\X\Y\Z-vis},
3d/hidden/.append style={postaction={store path=\X\Y\Z-hid}}]
pic{3d/circle on sphere={C={(I)},R=\myR,P={(i\X\Y\Z)}}};
\pgfmathtruncatemacro{\np}{tikztdindexoflastcoordinate}
\ifnum\np>0
\draw[3d/screen coords,3d/visible]
[stored path/first coordinate of=\X\Y\Z-hid] coordinate (tmpA)
[stored path/last coordinate of=\X\Y\Z-hid] coordinate (tmpB)
let \p1=($(tmpA)-(I)$),\p2=($(tmpB)-(I)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)},
\n3={(abs(\n1-\n2)>180?\n2+360:\n2)}
in (tmpA) arc[start angle=\n1,end angle=\n3,radius=\myR];
\fi
\tikzset{stored path/reset coordinate index}
\else
\path[3d/visible/.style={3d/hidden}] pic{3d/circle on sphere={C={(I)},R=\myR,P={(i\X\Y\Z)}}};
\fi}
\end{scope}
\end{tikzpicture}
\end{document}
```
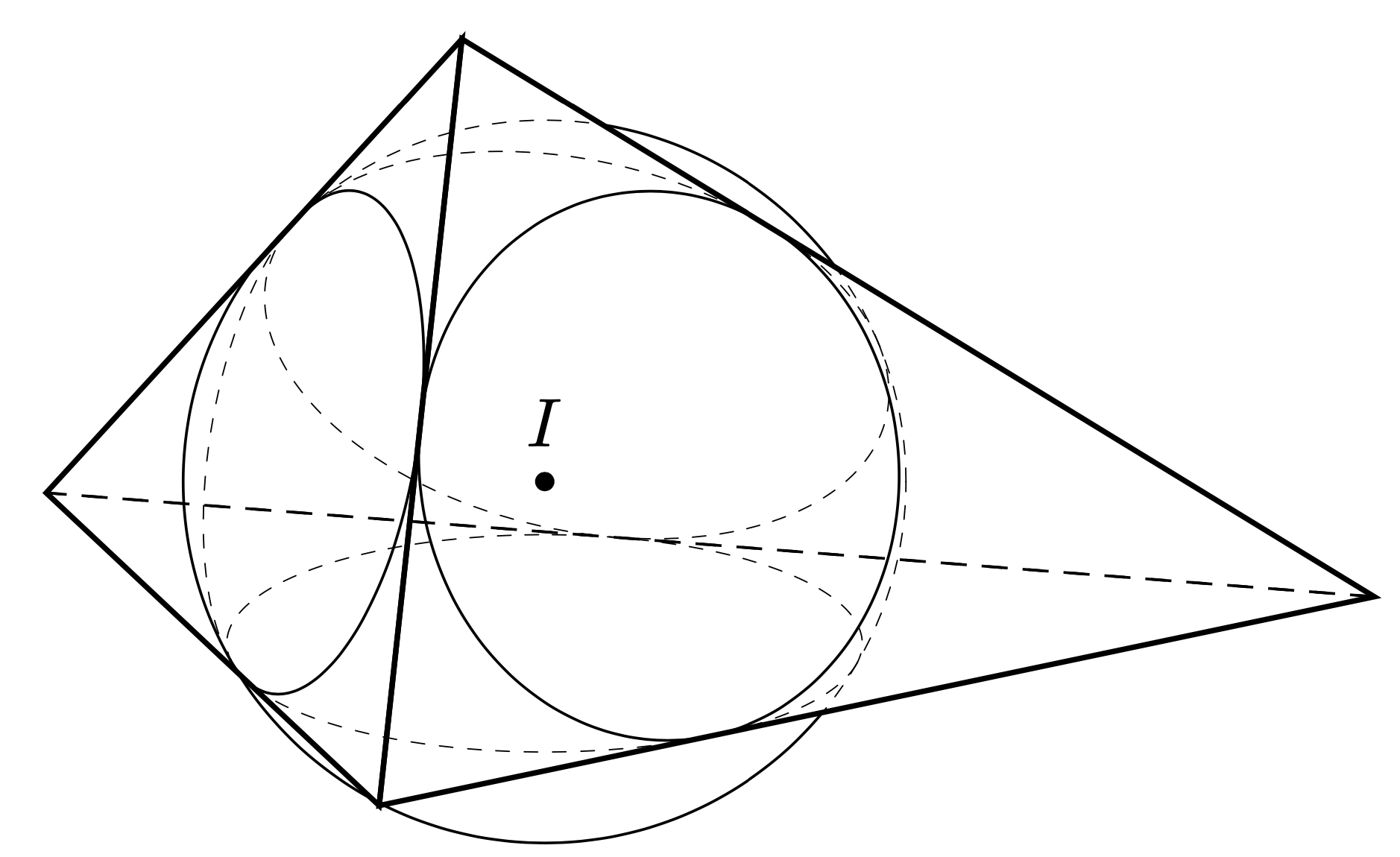
This code borrow some code from marmot.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) rectangle (12383.99999pt,12383.99999pt)}}}
\begin{document}
\begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,
line join=round,visible/.style={draw,solid},
hidden/.style={draw,very thin,cheating dash},
declare function={lAB=5;lAC=7;lBC=6;lAD=5;lBD=4;lCD=6;}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=70,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos(-1*(lBC*lBC-lAC*lAC-lAB*lAB)/(2*lAB*lAC))}
\path (0,0,0) coordinate (A)
(lAB,0,0) coordinate (B)
({lAC*cos(\mytheta)},{lAC*sin(\mytheta)},0) coordinate (C);
% cross checks
% \pgfmathsetmacro{\dAB}{tddistance("(A)","(B)")}%
% \pgfmathsetmacro{\dAC}{tddistance("(A)","(C)")}%
% \pgfmathsetmacro{\dBC}{tddistance("(B)","(C)")}%
% \typeout{\dAB,\dBC,\dAC}
\path[overlay,3d/aux keys/i1=D,3d/aux keys/i2=D',
3d/intersection of three spheres={rA=lAD,rB=lBD,rC=lCD}];
\path pic[red,hidden]{3d incircle={%
A={(A)},B={(B)},C={(C)}, center name = X}};
\path pic[orange,visible]{3d incircle={%
A={(A)},B={(B)},C={(D)}, center name = Y}};
\path pic[blue,hidden]{3d incircle={%
A={(A)},B={(D)},C={(C)}}};
\path pic[orange,visible]{3d incircle={%
A={(C)},B={(B)},C={(D)}}};
\path [overlay,
3d coordinate={(myn1)=(A)-(B)x(A)-(C)},
3d coordinate={(myn2)=(D)-(B)x(D)-(A)}];
\path[3d/line with direction={(myn1) through (X) named d1},
3d/line with direction={(myn2) through (Y) named d2}];
\path[3d/intersection of={d1 with d2}] coordinate (Z);
\path[3d/line through={(A) and (B) named lAB}];
\path[3d/project={(Z) on lAB}] coordinate (W);
\pgfmathsetmacro{\myR}{sqrt(TD("(Z)-(W)o(Z)-(W)"))}
%\shade[ball color=white,3d/screen coords] (Z) circle[radius=\myR];
\draw[3d/screen coords] (Z) circle[radius=\myR];
\begin{scope}
\clip[3d/screen coords] (Z) circle[radius=\myR][reverseclip];
\draw[visible] (D) -- (C);
\end{scope}
\begin{scope}
\clip[3d/screen coords] (Z) circle[radius=\myR];
\draw[hidden] (D) -- (C);
\end{scope}
\draw[hidden]
(A) -- (C) (X) -- (Z) -- (Y);
\draw [visible] (D) -- (A) -- (B) -- (C) (D) -- (B);
\foreach \p in {A,B,C,D,Z,X,Y}
{\draw[fill=black] (\p) circle (1.2 pt);}
\foreach \p/\g in {A/-90,B/-90,C/-90,D/90,Z/90,X/-90,Y/90}
{\path (\p)+(\g:3mm) node{$\p$};}
\end{scope}
\end{tikzpicture}
\end{document}
```