Another way to draw some balls in a cylinder. - TeX

TopAnswers TeX

Meta

Databases

TeX

Code Golf

APL

C++

.net

db<>fiddle

Java

*nix

PHP

PowerShell

Python

Rust

टेक्-मराठी

Typst

Web Client Dev

Web Server Dev

Another way to draw some balls in a cylinder.

add tag

Anonymous 1123

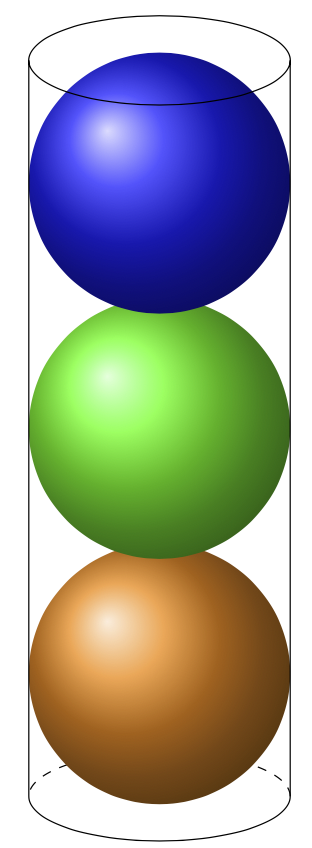
At [here](https://tex.stackexchange.com/questions/399112/how-can-i-draw-some-spheres-inside-a-cylinder/399246#399246) is question and answers about draw some balls in a cylinder. I tried with `\usepackage{tikz-3dplot}`
```
\documentclass[border=2mm,12pt,tikz]{standalone}
\usepackage{tikz-3dplot} 
\usetikzlibrary{3d,calc,backgrounds,patterns}
%\usepackage{fouriernc}
\begin{document}
	\def\myr{1.5}
	\def\h{6*\myr}
	\def\angA{0}
	\def\angB{110}
	\tdplotsetmaincoords{70}{70}
	\begin{tikzpicture}[tdplot_main_coords]
		\begin{scope}[canvas is xy plane at z=0]
			\draw[dashed] (\tdplotmainphi:\myr) arc(\tdplotmainphi:\tdplotmainphi+180:\myr);
			\coordinate (O) at (0,0);
			\coordinate (A) at (\angA:\myr);
			\coordinate (B) at (\angB:\myr);
			\coordinate (M) at ($(A)!0.5!(B)$);
			
			\draw[thick] (\tdplotmainphi:\myr) coordinate(BR) arc(\tdplotmainphi:\tdplotmainphi-180:\myr)
			coordinate(BL);
	
		\end{scope}
			\begin{scope}[canvas is xy plane at z=\h/3]
			\coordinate (O_1) at (0,0);
		\end{scope}
		
		\begin{scope}[canvas is xy plane at z=2/3*\h]
			\coordinate (O_2) at (0,0);
		\end{scope}
		
		\begin{scope}[canvas is xy plane at z=\h]
			
			\coordinate (O') at (0,0);
			\coordinate (A') at (\angA:\myr);
			\coordinate (B') at (\angB:\myr);
			\coordinate (M') at ($(A')!0.5!(B')$);
			
			\draw[thick]  (O') circle[radius=\myr];
			\draw[dashed] (O) -- (O');
			\draw [thick](BR) -- (\tdplotmainphi:\myr) (BL) -- (\tdplotmainphi-180:\myr); 
		\end{scope}
		
		\coordinate (T) at ($ (O) !0.5! (O_1) $);
		\coordinate (T1) at ($ (O_1) !0.5! (O_2) $);
		\coordinate (T2) at ($ (O_2) !0.5! (O') $);	
		\foreach \v/\position in {O/below,O'/above} {\draw[draw =black, fill=black] (\v) circle (1pt) node [\position=0.2mm] {$\v$};
		}
			\begin{scope}[tdplot_screen_coords, on background layer]
			\fill[ball color=orange!90, opacity=1.0] (T) circle (\myr); 
		\end{scope}
		
		\begin{scope}[tdplot_screen_coords, on background layer]
			\fill[ball color=green!90, opacity=1.0] (T1) circle (\myr); 
		\end{scope}
		\begin{scope}[tdplot_screen_coords, on background layer]
			\fill[ball color=blue!90, opacity=1.0] (T2) circle (\myr); 		\end{scope}
	\end{tikzpicture}
	
\end{document} 
```
 How to draw this with another way?
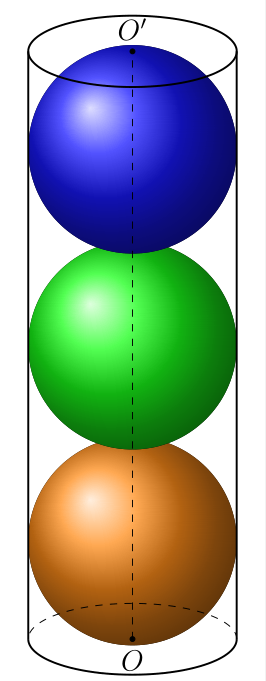
![ScreenHunter 1074.png](/image?hash=4d6f39b242eb8adaa8fff4b2eca6c186d46c53e3373576c5a56c8d8b18fa5fd4)

Top Answer

user 3.14159

I think your code is fine. This one is marginally shorter. 
```
\documentclass[border=2mm,12pt,tikz]{standalone}
\usepackage{tikz-3dplot} 
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}
\begin{document}
\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords,line cap=round,line join=round,
	  declare function={r=1.5;h=6*r;}]
	\path foreach \Z in {1,2,3}
	 {(0,0,-r+2*\Z*r) coordinate (C\Z)}
	 (0,0,0) coordinate (B) (0,0,h) coordinate (T);
	\path[tdplot_screen_coords] (r,0,0) coordinate(rx); 
	\pgfmathtruncatemacro{\itest}{(cos(\tdplotmaintheta)>0?1:0)}
	\begin{scope}[canvas is xy plane at z=0]
	    \ifnum\itest=1
		 \edef\myB{B}
		 \edef\myT{T}
		\else
		 \edef\myB{T}
		 \edef\myT{B}
		\fi
		\begin{pgfonlayer}{background}
		 \draw[dashed] let \p1=(rx),\n1={atan2(\y1,\x1)} in 
			($(\myB)+(\n1:r)$) arc[start angle=\n1,end angle=\n1+180,radius=r];
		\end{pgfonlayer}
		\begin{pgfonlayer}{foreground}
		 \draw let \p1=(rx),\n1={atan2(\y1,\x1)} in 
		 ($(\myB)+(\n1:r)$) arc[start angle=\n1,end angle=\n1-180,radius=r]
		 ($(\myB)+(rx)$) -- ($(\myT)+(rx)$)
		   ($(\myB)-(rx)$) -- ($(\myT)-(rx)$)
		   (\myT) circle[radius=r];
		\end{pgfonlayer}
	\end{scope}
	\begin{scope}[tdplot_screen_coords]
	 \foreach \Col [count=\Z] in {orange!90,green!90,blue!90}
	 {\shade[ball color=\Col] (C\Z) circle[radius=r];}
	\end{scope}
\end{tikzpicture}
\end{document}
```
![Screen Shot 2021-01-12 at 9.23.11 PM.png](/image?hash=57acaeca8b5350521cf4577a14f9214f60dd31db5783db5d58b2bd38d90fce6a)

1 Answer