First of all, at the moment I do not have a general method. Let us first explain why the polyhedron stuff does not give a good result here: the shape is not convex.
One may think that one could just order the faces appropriately. This may be a good idea but it is actually not so easy to find a correct ordering prescription. Things that do not work in general include:
1. sorting according to the screen depth of the barycenters of the faces.
2. sorting according to the maximal screen depth of the vertices of the faces.
The second method "almost" works but since these faces share vertices one has degeneracies for which it is nontrivial to come up with a general ordering prescription.
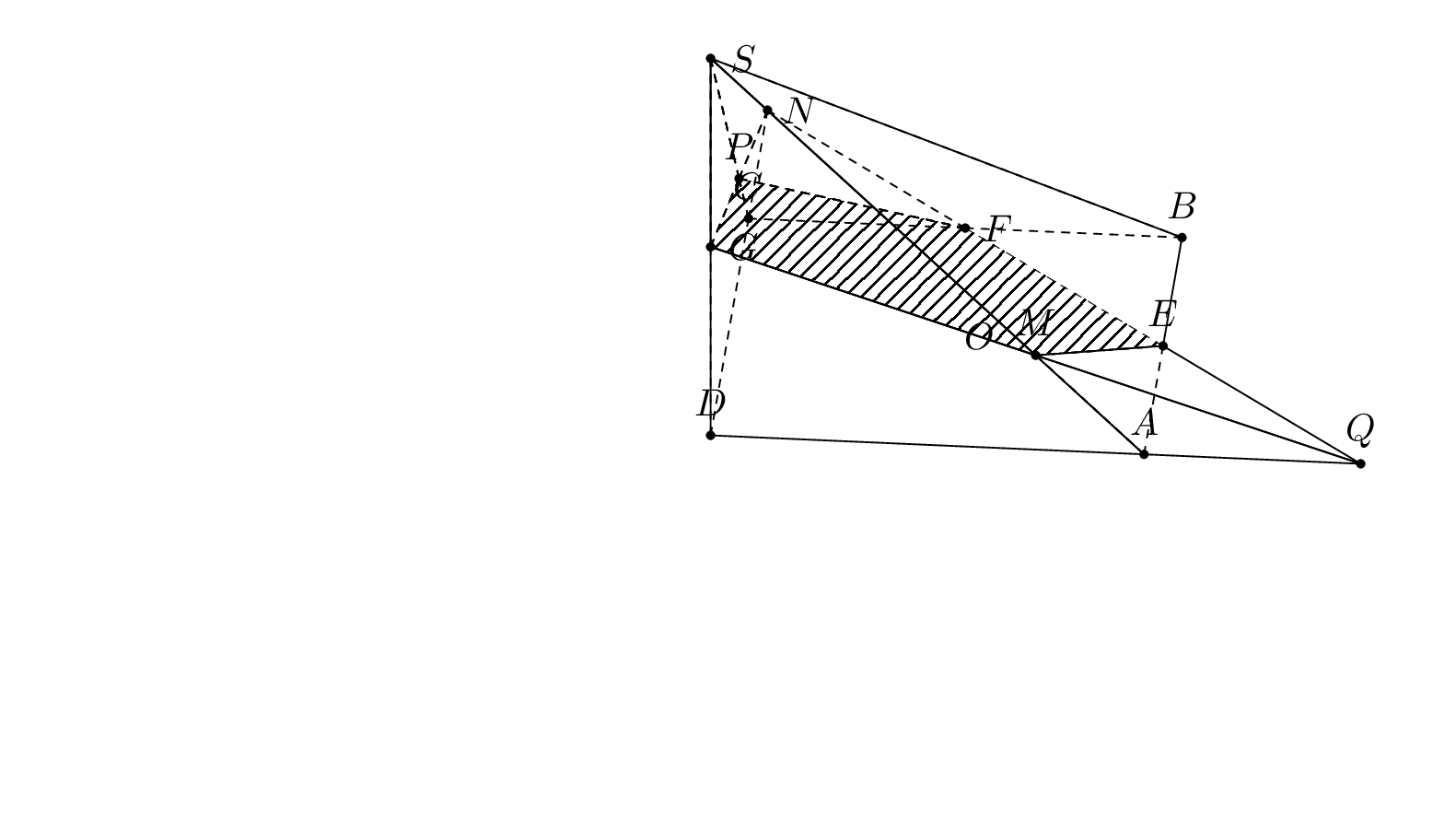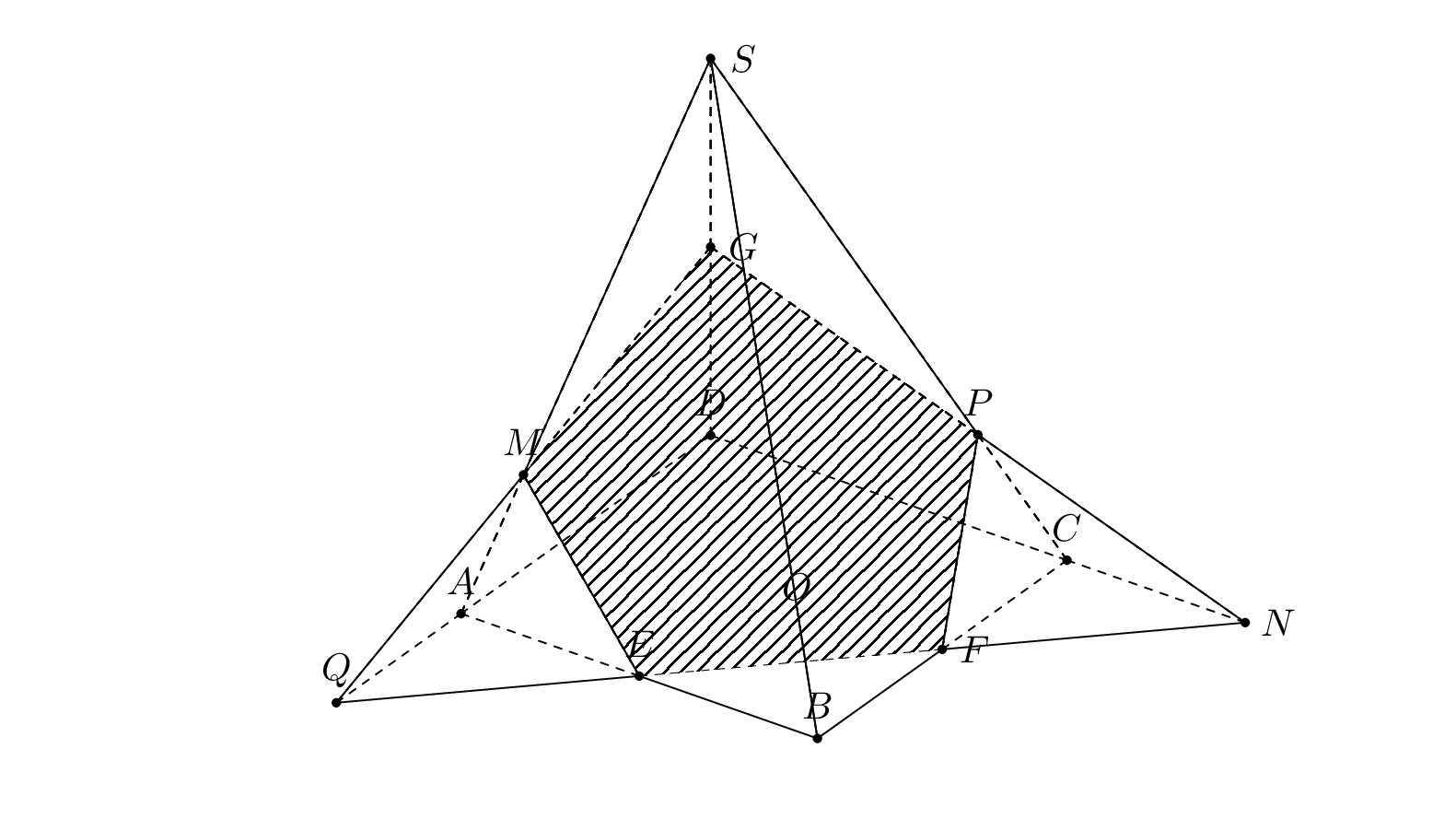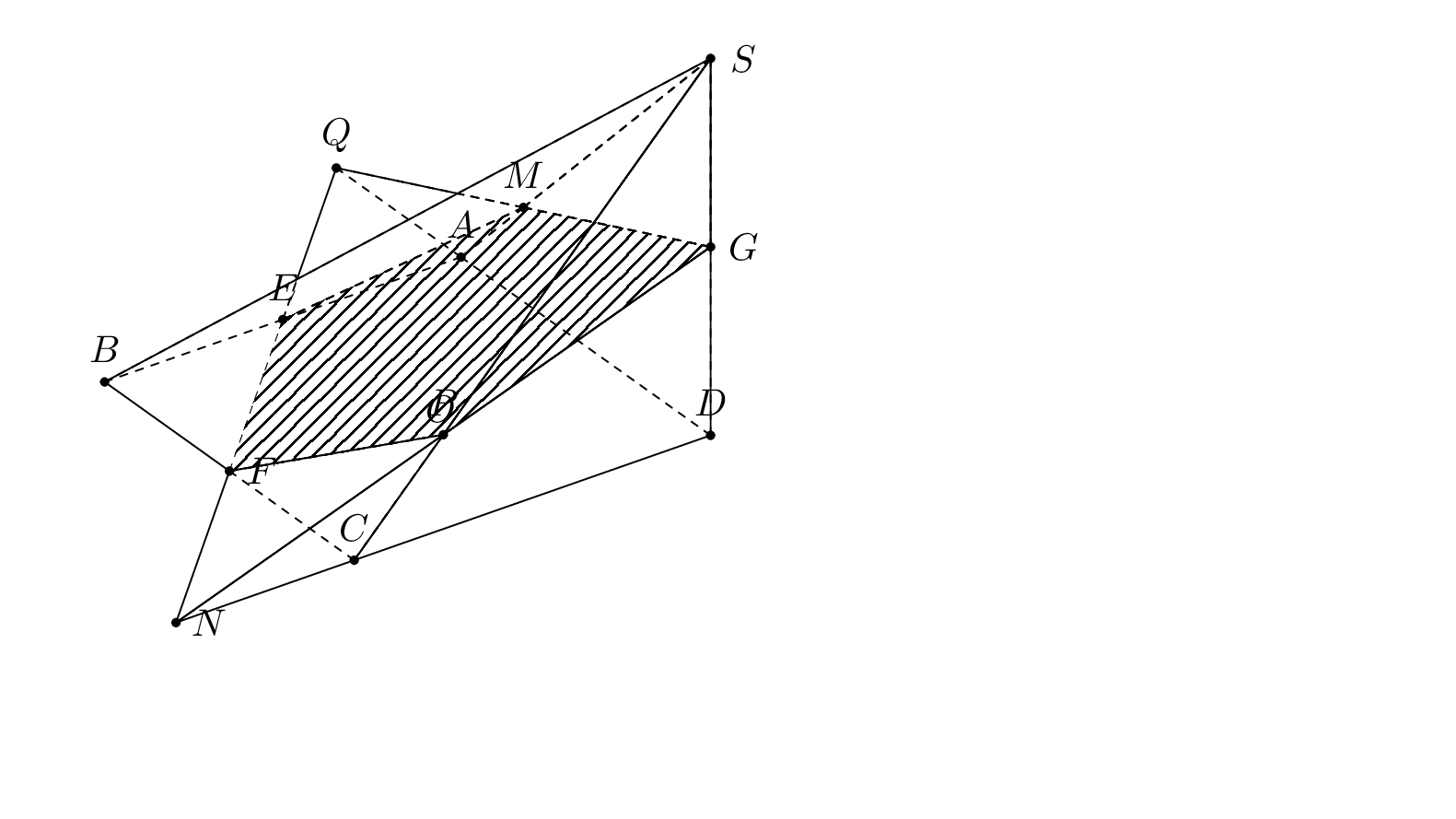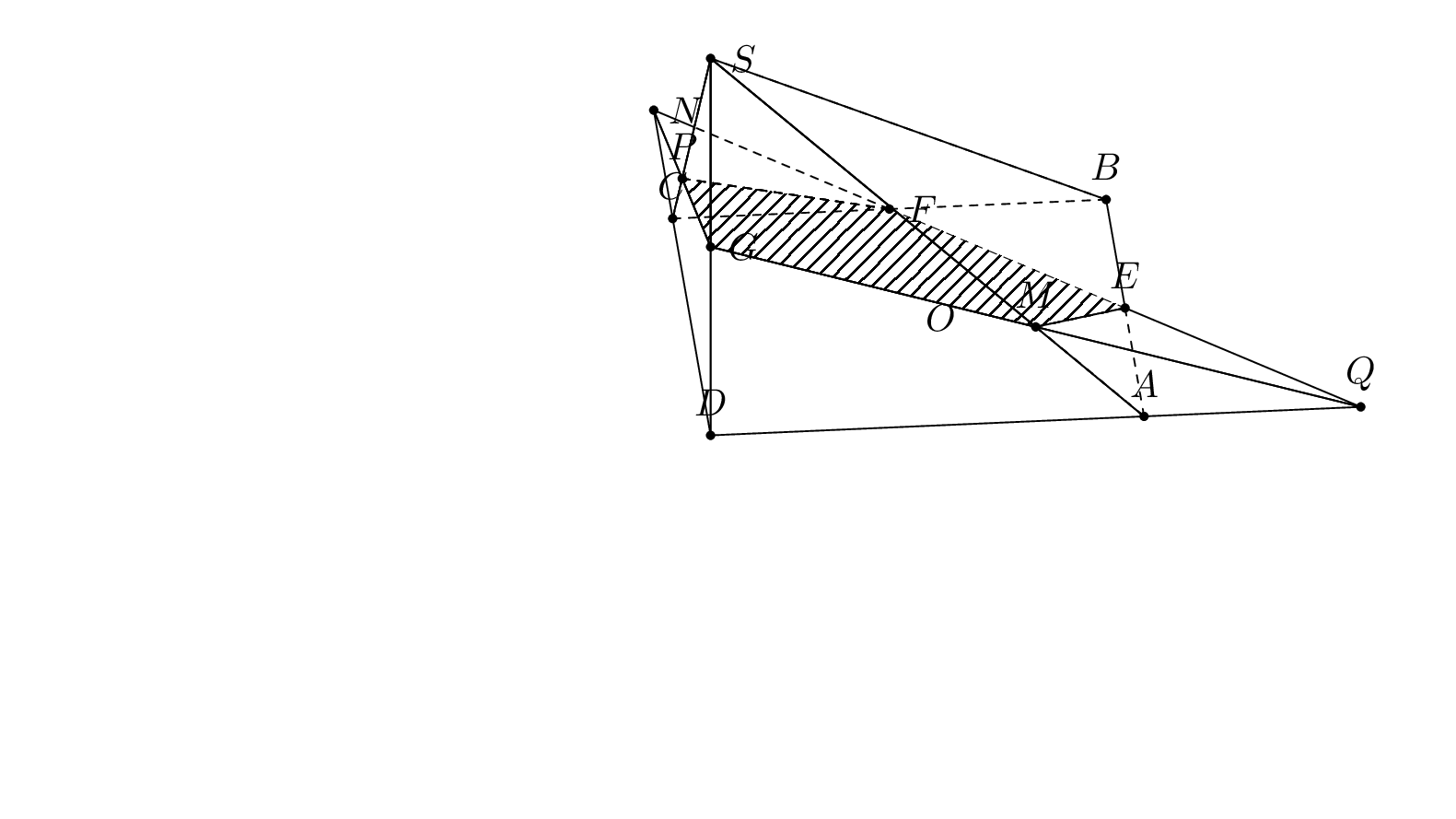
The problem at hand can be solved by drawing three polyhedra, `AEMQ`, `CFPN`, and the big remaining one contained in `ABCDS`, in an appropriate order and using reverse clips. However, this is not a general method, it only works in simple enough cases. The criteria are:
1. if the outward normal `nABS` has positive screen depth, draw `AEMQ` in front of `ABCDS`, otherwise draw `ABCDS` in front of `AEMQ`.
2. if the outward normal `nBBS` has positive screen depth, draw `CFNP` in front of `ABCDS`, otherwise draw `ABCDS` in front of `CFNP`.
3. if the barycenter of `AEMQ` has greater screen depth than the barycenter of `CFNP`, draw `AEMQ` in front of `CFNP`, otherwise reverse the order.
Here is some excessive code that requires the latest version of the [`3dtools` library](https://github.com/marmotghost/tikz-3dtools).
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{patterns.meta}
\usetikzlibrary{3dtools} % https://github.com/marmotghost/tikz-3dtools
\makeatletter
\newif\if@pgf@list@first@item
\pgfkeys{/handlers/.add item/.code=\pgfkeys{\pgfkeyscurrentpath/.append={,#1}},
/handlers/.remove item/.code={%
\edef\pgfutil@tmpa{\pgfkeysvalueof{\pgfkeyscurrentpath}}%
\edef\pgfutil@tmpb{#1}%
\edef\pgfutil@tmpc{\noexpand\@removeelement{\pgfutil@tmpb}{\pgfutil@tmpa}{\noexpand\pgfutil@tmpa}}%
\pgfutil@tmpc
\pgfkeyssetvalue{\pgfkeyscurrentpath}{\pgfutil@tmpa}},% maybe test if the list is now empty?
}
\tikzset{3d/draw behind/.code 2 args={% #1 object, #2 list of objects in front
%\typeout{Draw #1 behind #2.}
\tikzset{3d/current path=#1,
3d/draw clipped against/.list={#2},
3d/draw avoiding={#2}}
},3d/draw clipped against/.code={% #1=clip path
%\typeout{Clip \pgfkeysvalueof{/tikz/3d/current path} against #1.}
\begin{scope}
\tikzset{/tikz/3d/polyhedron/before hidden/.code={%\typeout{clip!}%
\clip[use named path/.expanded=#1];},
/tikz/3d/polyhedron/before visible/.code={%\typeout{clip!}%
\clip[use named path/.expanded=#1];},
all hidden,
/tikz/polyhedron \pgfkeysvalueof{/tikz/3d/current path}}
\end{scope}},
3d/draw avoiding/.code={% #1=list of paths to be avoided
%\typeout{Draw \pgfkeysvalueof{/tikz/3d/current path} avoiding #1.}
\begin{scope}
\tikzset{protect/.list={#1}}
\tikzset{/tikz/3d/polyhedron/before hidden/.code={%\typeout{avoid!}%
\tikzset{protect/.list={#1}}},
/tikz/3d/polyhedron/before visible/.code={%\typeout{avoid #1!}%
\tikzset{protect/.list={#1}}},
/tikz/polyhedron \pgfkeysvalueof{/tikz/3d/current path}}
\end{scope}},3d/current path/.initial={},
3d/draw ordered objects/.code={%
\tikzset{3d/temporary list 1/.initial={#1},
3d/draw ordered object/.list={#1}}%
},3d/draw ordered object/.code={%
% test if remaining list has only one element
\edef\pgf@util@tempa{\noexpand\pgfutil@in@{,}{\pgfkeysvalueof{/tikz/3d/temporary list 1}}}%
\pgf@util@tempa
\tikzset{3d/temporary list 1/.remove item={#1}}
\ifpgfutil@in@%
\tikzset{3d/draw behind/.expanded={#1}{\pgfkeysvalueof{/tikz/3d/temporary list 1}}}
\else
\begin{scope}
\tikzset{polyhedron #1};
\end{scope}
\fi
}}
\makeatother
\tikzset{
protect/.code={%\typeout{protecting #1.}
\clip[overlay,reset cm,even odd clip,use named path=#1]
(-16383.99999pt,-16383.99999pt) rectangle (16383.99999pt,16383.99999pt);
}}
\begin{document}
\foreach \Angle in {5,15,...,355} % {5,25,...,355} % {345} % {55} % {155} %
{\tdplotsetmaincoords{60}{\Angle}
\begin{tikzpicture}[same bounding box=A,%<- newly added to `3dtools`
scale=1,tdplot_main_coords,line join = round,
line cap = round, declare function={a = 4;b = 4;h=4;}]
\path
(0,0,0) coordinate (D)
(a,0,0) coordinate (A)
(a,b,0) coordinate (B)
(0,b,0) coordinate (C)
(0,0,h) coordinate (S)
(a/2,b/2,h/8) coordinate (O')
[3d coordinate = {(E) = 0.5*(A) + 0.5*(B)},
3d coordinate = {(F) = 0.5*(B) + 0.5*(C)},
3d coordinate = {(G) = 0.5*(D) + 0.5*(S)},
3d coordinate = {(O) = 0.5*(A) + 0.5*(C)}];
\path[3d/plane through=(E) and (F) and (G) named pEFG];
\path[3d/line through={(S) and (A) named lSA}];
\path[3d/line through={(C) and (D) named lCD}];
\path[3d/line through={(S) and (C) named lSC}];
\path[3d/line through={(A) and (D) named lAD}];
\path[3d/intersection of={lSA with pEFG}] coordinate (M);
\path[3d/intersection of={lCD with pEFG}] coordinate (N);
\path[3d/intersection of={lSC with pEFG}] coordinate (P);
\path[3d/intersection of={lAD with pEFG}] coordinate (Q);
\foreach \p in {A,B,C,D,M,P,Q,S,E,F,G,N}
{\draw[fill=black] (\p) circle (1pt);}
\foreach \p/\g in {A/90,B/90,C/90,D/90,M/90,P/90,Q/90,E/90,F/0,G/0,S/0,N/0,O/0}
{\path (\p)+(\g:3mm) node{$\p$};}
\path[pattern={Lines[angle=45]}] (E) -- (F) -- (P) -- (G) -- (M) -- cycle;
%
\pgfmathsetmacro{\mybarycenterAEMQ}{barycenter("(A),(E),(M),(Q)")}
\path (\mybarycenterAEMQ) coordinate (OAEMQ);
\pgfmathsetmacro{\sdAEMQ}{screendepth(\mybarycenterAEMQ)}
\pgfmathsetmacro{\nAEMQ}{TD("(A)-(B)x(A)-(S)")}
\pgfmathtruncatemacro{\itest}{sign(TD("(A)-(O')o(\nAEMQ)"))}
\ifnum\itest<0
\pgfmathsetmacro{\nAEMQ}{TD("(B)-(A)x(A)-(S)")}
\fi
%
\pgfmathsetmacro{\mybarycenterCFNP}{barycenter("(C),(F),(N),(P)")}
\path (\mybarycenterCFNP) coordinate (OCFNP);
\pgfmathsetmacro{\sdCFNP}{screendepth(\mybarycenterCFNP)}
\pgfmathsetmacro{\nCFNP}{TD("(C)-(B)x(C)-(S)")}
\pgfmathtruncatemacro{\itest}{sign(TD("(B)-(O')o(\nCFNP)"))}
\ifnum\itest<0
\pgfmathsetmacro{\nCFNP}{TD("(B)-(C)x(C)-(S)")}
\fi
%
\tikzset{3d/polyhedron/.cd,
%face edges/.style={},%
back/.style={3d/polyhedron/complete dashes,fill=none},
%
fore/.style={3d/visible,solid,fill=none,
3d/polyhedron/edges have complete dashes=false},
complete dashes,
/tikz/all hidden/.style={%
3d/polyhedron/fore/.style={3d/polyhedron/complete dashes,fill=none},
}}
\path[save named path=ABCDS,convex hull of={A,B,C,D,S}];
\path[save named path=AEMQ,convex hull of={A,E,M,Q}];
\path[save named path=CFNP,convex hull of={C,F,N,P}];
\tikzset{polyhedron ABCDS/.style={%
/tikz/3d/polyhedron/.cd,
O={(O')},
draw face with corners={{(B)},{(E)},{(M)},{(S)}},
draw face with corners={{(B)},{(F)},{(P)},{(S)}},
draw face with corners={{(A)},{(D)},{(G)},{(M)}},
draw face with corners={{(M)},{(G)},{(S)}},
draw face with corners={{(C)},{(D)},{(G)},{(P)}},
draw face with corners={{(P)},{(G)},{(S)}},
draw face with corners={{(G)},{(M)},{(S)}},
draw face with corners={{(G)},{(P)},{(S)}},
},
polyhedron AEMQ/.style={%
/tikz/3d/polyhedron/.cd,
O={(OAEMQ)},
draw face with corners={{(A)},{(M)},{(Q)}},
draw face with corners={{(E)},{(M)},{(Q)}},
draw face with corners={{(A)},{(E)},{(M)}},
},
polyhedron CFNP/.style={%
/tikz/3d/polyhedron/.cd,
O={(OCFNP)},
draw face with corners={{(C)},{(P)},{(N)}},
draw face with corners={{(F)},{(P)},{(N)}},
draw face with corners={{(C)},{(F)},{(P)}},
},
}
\pgfmathtruncatemacro{\itest}{(screendepth(\nAEMQ)>0?1:0)}
\pgfmathtruncatemacro{\jtest}{(screendepth(\nCFNP)>0?1:0)}
\pgfmathtruncatemacro{\ktest}{(\sdAEMQ>\sdCFNP?1:0)}
\pgfmathtruncatemacro{\icase}{3*\itest+2*\jtest+\ktest}
%\typeout{\Angle:\icase}
\ifcase\icase
\tikzset{3d/draw ordered objects/.expanded={AEMQ,CFNP,ABCDS}}
\or
\tikzset{3d/draw ordered objects/.expanded={CFNP,AEMQ,ABCDS}}
\or
\tikzset{3d/draw ordered objects/.expanded={AEMQ,ABCDS,CFNP}}
\or
\or
\tikzset{3d/draw ordered objects/.expanded={CFNP,ABCDS,AEMQ}}
\or
\tikzset{3d/draw ordered objects/.expanded={ABCDS,AEMQ,CFNP}}
\or
\tikzset{3d/draw ordered objects/.expanded={ABCDS,CFNP,AEMQ}}
\fi
%
\draw[3d/hidden] (E) --(F);
%\path (current bounding box.north west) node[below right] {$\alpha=\Angle$, $i=\icase$};
\end{tikzpicture}}
\end{document}
```