Consider I have a transfer function (polynomial fraction)
```
a_1*s^n + a_2*s^{n-1} + ... + a_{n-1}*s^1 + a_n
---------------------------------------------
s^N + b_1*s^{N-1} + ... + b_{N-1}*s^1 + b_N
```
where the denominator order `N` is greater than the numerator order `n`.
I would like to find a robust way to transform it to a matrix `\StateMat` representing the phase variable form of the state-space to have
```
\edef\StateMat{%
{ 0 , 1 , 0 , 0 , ... , 0 },%
{ 0 , 0 , 1 , 0 , ... , 0 },%
{ 0 , 0 , 0 , 1 , ... , 0 },%
% .........................
{ 0 , 0 , 0 , ... , 0 , 1 },%
{ -b_N , -b_{N-1} , ... , -b_1 },%
{ a_n , a_{n-1} , ... , 0 }%
}
```
where the matrix is square of dimensions `N+1`*`N+1`.
The expected input from my side is two matrices of the coefficients
```
\edef\NumCoeffMat{%
{ a_1 , a_2 , ... , a_n }%
}
```
and
```
\edef\DenCoeffMat{%
{ b_1 , b_2 , ... , b_N }%
}
```
---
# Edit (after marmot's answer)
This problem is a part of converting a transfer function into a state space representation for drawing the signal flow graphs introduced here https://topanswers.xyz/tex?q=1568#a1818
## Full MWE
```
\documentclass[tikz,border=5mm]{standalone}
\usetikzlibrary{calc,decorations.markings,positioning,arrows.meta}
\usepackage{pgffor}
\makeatletter
\pgfkeys{/matrix games/.cd,
count/.code={\c@pgf@counta0\relax
\pgfkeys{/matrix games/step counta/.list/.expanded={#1}}%
\edef\pgfmathresult{\the\c@pgf@counta}%
},step counta/.code={\advance\c@pgf@counta by1\relax},
cells/.code={\pgfmathparse{#1}},nrows/.initial=5,ncols/.initial=5,
create matrix/.code={\edef\pgf@util@tempa{}%
\foreach \i in {1,...,\pgfkeysvalueof{/matrix games/nrows}}%
{\foreach \j in {1,...,\pgfkeysvalueof{/matrix games/ncols}}{%
\pgfkeys{/matrix games/cells}%
\ifnum\j=1\relax
\xdef\pgf@util@tempb{\pgfmathresult}%
\else
\xdef\pgf@util@tempb{\pgf@util@tempb,\pgfmathresult}%
\fi}%
\ifnum\i=1\relax
\xdef\pgf@util@tempa{{\pgf@util@tempb}}%
\else
\xdef\pgf@util@tempa{\pgf@util@tempa,{\pgf@util@tempb}}%
\fi}%
\let#1\pgf@util@tempa
}}
\makeatother
\begin{document}
\edef\NumCoeffMat{{2,24,34}}%
\edef\DenCoeffMat{{10,31,30}}%
\pgfkeys{/matrix games/.cd,count=\NumCoeffMat}%
\pgfmathtruncatemacro\myN{\pgfmathresult+1}% now \myN is 1 + the length of \NumCoeffMat
\pgfkeys{/matrix games/.cd,count=\DenCoeffMat}%
\pgfmathtruncatemacro\myM{\pgfmathresult}% now \myM is the length of \DenCoeffMat
\pgfkeys{/matrix games/.cd,ncols=\myN,nrows=\numexpr\myN+1,
cells/.code={
\pgfmathtruncatemacro{\icase}{(\i==\myN?1:0)+(\i==\myN+1?2:0)}%
\ifcase\icase% first case: zero unless \i+1=\j
\pgfmathparse{int(\i+1==\j?1:0)}%
\or% second case
\ifnum\j>\numexpr\myN-1\relax% subcase a) \j >=\myN
\pgfmathparse{1}%
\else% subcase b) \j <\myN (fill in \NumCoeffMat reversed)
\pgfmathparse{int(\NumCoeffMat[\myN-\j-1])}%
\fi
\or% third case
\ifnum\j<\numexpr\myM+1\relax% subcase a) \j <=\myM (fill in \DenCoeffMat reversed)
\pgfmathparse{int(\DenCoeffMat[\j-1])}%
\else% subcase b) \j > \myN (fill in zeros)
\pgfmathparse{int(0)}%
\fi
\fi},
create matrix=\StateMat}%
\begin{tikzpicture}[node distance = 15 mm,
amark/.style={
decoration={
markings,
mark=at position {0.5} with {
\arrow{stealth},
}
},
postaction={decorate,edge label={#1}}
}, % make the mark an entry of the \StateMat matrix
pmark/.code n args={2}{%
\pgfmathtruncatemacro{\myi}{int({\StateMat}[\numexpr#1][\numexpr#2])}%
\tikzset{suppress if 0=\myi,edge label={$\myi$},
amark}% <- changed
},
terminal/.style 2 args={draw,alias=ln,circle,inner sep=2pt,label={#1:#2}},
% semicircle path
semicircle/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.north) arc[start angle=180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.south) arc[start angle=0,end angle=-180,radius=-0.5*\x1]
\fi
\tikztonodes}},
semicircle'/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.south) arc[start angle=-180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.north) arc[start angle=0,end angle=180,radius=-0.5*\x1]
\fi
\tikztonodes}},
add key if/.code n args={3}{\pgfmathtruncatemacro{\itest}{(#1?0:1)}%
\ifcase\itest
\tikzset{#2}%
\else
\tikzset{#3}%
\fi
},suppress if 0/.style={add key if={#1==0}{opacity=0}{}}
]
\pgfmathtruncatemacro{\dimy}{dim({\StateMat})} % number of rows
\pgfmathtruncatemacro{\dimx}{dim({\StateMat}[0])} % number of columns
% create the graph
\path % R node
node[terminal={left}{$R(S)$},alias={X-\dimy}] (R) {}
% loop over matrix entries
foreach \Y [evaluate=\Y as \X using {int(\dimy-\Y)}]
in {1,...,\numexpr\dimy-1}
{node[right=of ln,terminal={below right}{% sX_i node
$sX_{\X}(s)$}](sX-\X){}
node[right=of ln,terminal={below right}{% X_i node
$X_{\X}(s)$}](X-\X){}
% ege from sX_i to X_i
(sX-\X) edge[amark,edge label={$\frac{1}{s}$}] (X-\X)
% edge from X_{i+1} to X_i (R had an alias)
(X-\the\numexpr\X+1) edge[pmark={\X-1}{\X}] (sX-\X)
% semicircle edge from X_i to sX_i
(X-\X) edge[semicircle,pmark={\X-1}{\X-1}] (sX-\X)
}
node[right=of ln,terminal={right}{$Y(s)$},alias=sX-\dimy](Y){}
(X-1) edge[pmark={\dimy-1}{0}] (Y)
% we are now done with the horizontal part,
% and have also dealt with the entries on the diagonal and
% the {i-1},i entries
% now we deal with the matrix entries
foreach \X in {1,...,\the\numexpr\dimx-1}
{% all edges that end in Y (excluding the horizontal one)
\ifnum\X>\numexpr1\relax
(X-\X) edge[pmark={\dimx-1}{\X-1},semicircle] (Y)
\fi
% all edges that start at R (excluding the horizontal one)
\ifnum\X<\numexpr\dimx-1\relax
(R) edge[pmark={\X-1}{\dimx-1},semicircle] (sX-\X)
\fi
% remaining semicircles
foreach \Y in {\the\numexpr\X+1,...,\dimy}
{% backwards pointing semicircles
\unless\ifnum\X\Y=1\dimy
(X-\X) edge[pmark={\Y-1}{\X-1},semicircle] (sX-\Y)
\fi
% forward pointing semicircles
\pgfextra{\pgfmathtruncatemacro{\itest}{(\Y<\dimy&&\Y-\X>1?1:0)}}
\ifnum\itest=\numexpr1\relax
(X-\Y) edge[swap,pmark={\X-1}{\Y-1},semicircle'] (sX-\X)
\fi
}
};
\end{tikzpicture}
\end{document}
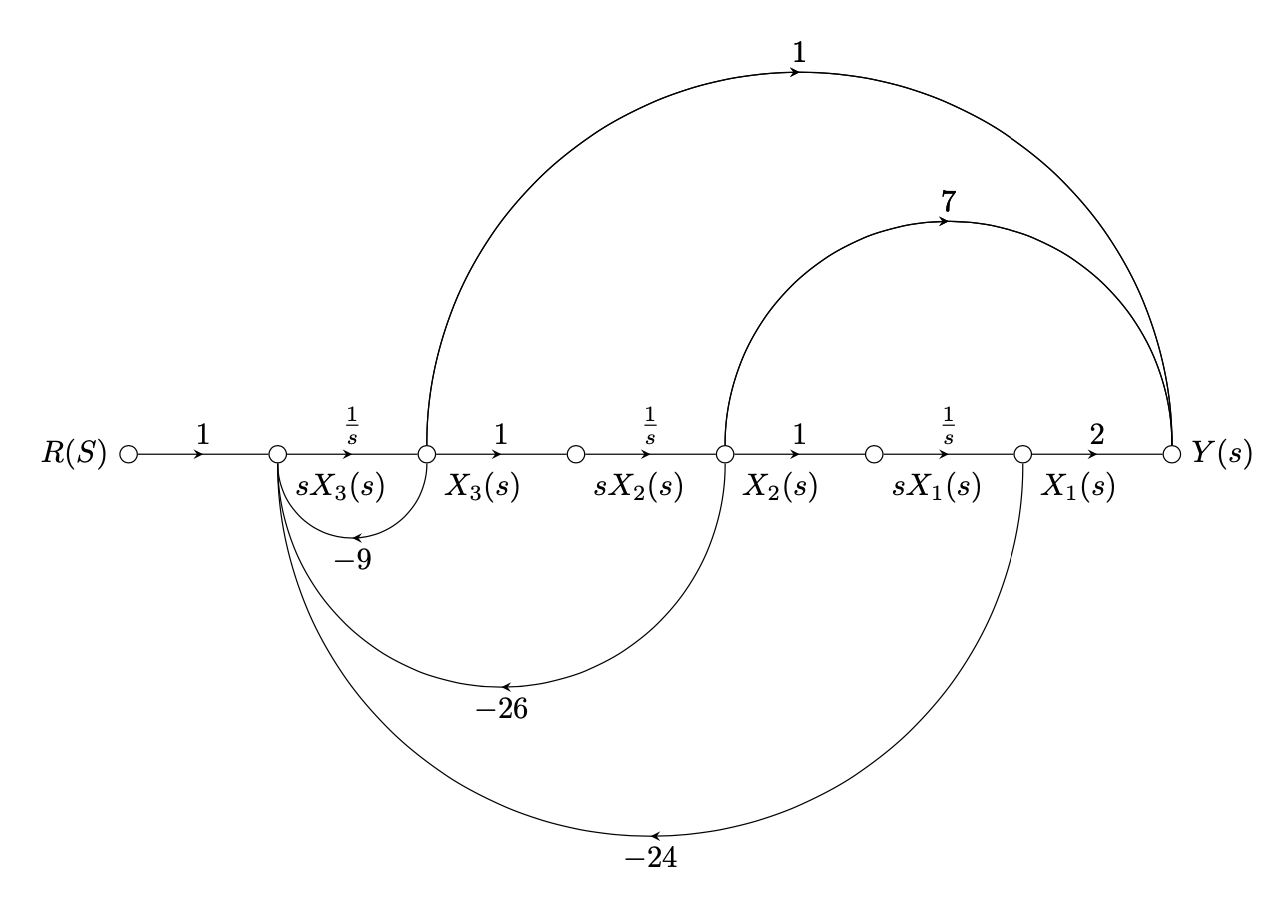
```Not sure if this qualifies for an answer. It uses global macros (though hidden ones) etc. This can all be avoided with the `/.list` key handler but the overhead might be too confusing without an explicit manula so this has to wait.
However, I tried to add some explanations for what is going on so that one can apply this to similar scenarios. There are two steps:
1. count the entries of the two lists `\NumCoeffMat` and `\DenCoeffMat`. This can be done with the `/.list` key handler without introducing explicit global macros (thus falsifying the claims that the Ti*k*Z `foreach` cannot do that, even nesting is fine).
2. use this information to fill the matrix programmatically. (With the `/.list` key handler one can even build LaTeX matrices with `&` and so on, but spelling this out is not relevant for this post.)
```
\documentclass{article}
\usepackage{pgffor}
\makeatletter
\pgfkeys{/matrix games/.cd,
count/.code={\c@pgf@counta0\relax
\pgfkeys{/matrix games/step counta/.list/.expanded={#1}}%
\edef\pgfmathresult{\the\c@pgf@counta}%
},step counta/.code={\advance\c@pgf@counta by1\relax},
cells/.code={\pgfmathparse{#1}},nrows/.initial=5,ncols/.initial=5,
create matrix/.code={\edef\pgf@util@tempa{}%
\foreach \i in {1,...,\pgfkeysvalueof{/matrix games/nrows}}%
{\foreach \j in {1,...,\pgfkeysvalueof{/matrix games/ncols}}{%
\pgfkeys{/matrix games/cells}%
\ifnum\j=1\relax
\xdef\pgf@util@tempb{\pgfmathresult}%
\else
\xdef\pgf@util@tempb{\pgf@util@tempb,\pgfmathresult}%
\fi}%
\ifnum\i=1\relax
\xdef\pgf@util@tempa{{\pgf@util@tempb}}%
\else
\xdef\pgf@util@tempa{\pgf@util@tempa,{\pgf@util@tempb}}%
\fi}%
\let#1\pgf@util@tempa
}}
\makeatother
\begin{document}
\edef\NumCoeffMat{{1,7,2}}%
\edef\DenCoeffMat{{9,26,24}}%
\pgfkeys{/matrix games/.cd,count=\DenCoeffMat}%
\pgfmathtruncatemacro\myN{\pgfmathresult}% now \myN is the length of \NumCoeffMat
\pgfkeys{/matrix games/.cd,count=\NumCoeffMat}%
\pgfmathtruncatemacro\myM{\pgfmathresult}% now \myM is the length of \DenCoeffMat
\pgfkeys{/matrix games/.cd,ncols=\numexpr\myN+1,nrows=\numexpr\myN+1,
cells/.code={% we now tell the matrix what to do depending on the row index \i
% and the column index \j
% there are three cases:
% 1. \i<\myN (the diagonal block)
% 2. \i=\myN (the row filled with \NumCoeffMat reversed)
% 3. \i=\myN+1 (the row filled with \DenCoeffMat)
\pgfmathtruncatemacro{\icase}{(\i==\myN?1:0)+(\i==\myN+1?2:0)}%
\ifcase\icase% first case: zero unless \i+1=\j
\pgfmathparse{int(\i+1==\j?1:0)}%
\or% second case
\ifnum\j>\numexpr\myN\relax% subcase a) \j >=\myN
\pgfmathparse{1}%
\else% subcase b) \j <\myN (fill in \NumCoeffMat reversed)
\pgfmathparse{int(-1*(\DenCoeffMat[\myN-\j]))}%
\fi
\or% third case
\ifnum\j<\numexpr\myM+1\relax% subcase a) \j <=\myM (fill in \DenCoeffMat reversed)
\pgfmathparse{int(\NumCoeffMat[\myM-\j])}%
\else% subcase b) \j > \myN (fill in zeros)
\pgfmathparse{int(0)}%
\fi
\fi},
create matrix=\StateMat}%
\StateMat
\typeout{\StateMat}
\end{document}
```
Of course this can be used in other codes.
```
\documentclass[tikz,border=5mm]{standalone}
\usetikzlibrary{calc,decorations.markings,positioning,arrows.meta}
\makeatletter
\pgfkeys{/matrix games/.cd,
count/.code={\c@pgf@counta0\relax
\pgfkeys{/matrix games/step counta/.list/.expanded={#1}}%
\edef\pgfmathresult{\the\c@pgf@counta}%
},step counta/.code={\advance\c@pgf@counta by1\relax},
cells/.code={\pgfmathparse{#1}},nrows/.initial=5,ncols/.initial=5,
create matrix/.code={\edef\pgf@util@tempa{}%
\foreach \i in {1,...,\pgfkeysvalueof{/matrix games/nrows}}%
{\foreach \j in {1,...,\pgfkeysvalueof{/matrix games/ncols}}{%
\pgfkeys{/matrix games/cells}%
\ifnum\j=1\relax
\xdef\pgf@util@tempb{\pgfmathresult}%
\else
\xdef\pgf@util@tempb{\pgf@util@tempb,\pgfmathresult}%
\fi}%
\ifnum\i=1\relax
\xdef\pgf@util@tempa{{\pgf@util@tempb}}%
\else
\xdef\pgf@util@tempa{\pgf@util@tempa,{\pgf@util@tempb}}%
\fi}%
\let#1\pgf@util@tempa
}}
\makeatother
\begin{document}
\edef\DenCoeffMat{{9,26,24}}%
\edef\NumCoeffMat{{1,7,2}}%
\pgfkeys{/matrix games/.cd,count=\DenCoeffMat}%
\pgfmathtruncatemacro\myN{\pgfmathresult}% now \myN is the length of \NumCoeffMat
\pgfkeys{/matrix games/.cd,count=\NumCoeffMat}%
\pgfmathtruncatemacro\myM{\pgfmathresult}% now \myM is the length of \DenCoeffMat
\pgfkeys{/matrix games/.cd,ncols=\numexpr\myN+1,nrows=\numexpr\myN+1,
cells/.code={% we now tell the matrix what to do depending on the row index \i
\pgfmathtruncatemacro{\icase}{(\i==\myN?1:0)+(\i==\myN+1?2:0)}%
\ifcase\icase% first case: zero unless \i+1=\j
\pgfmathparse{int(\i+1==\j?1:0)}%
\or% second case
\ifnum\j>\numexpr\myN\relax%
\pgfmathparse{1}%
\else%
\pgfmathparse{int(-1*(\DenCoeffMat[\myN-\j]))}%
\fi
\or% third case
\ifnum\j<\numexpr\myM+1\relax%
\pgfmathparse{int(\NumCoeffMat[\myM-\j])}%
\else%
\pgfmathparse{int(0)}%
\fi
\fi},
create matrix=\StateMat}%
\let\mmat\StateMat
\typeout{\StateMat}
\begin{tikzpicture}[node distance = 15 mm,
amark/.style={
decoration={
markings,
mark=at position {0.5} with {
\arrow{stealth},
}
},
postaction={decorate,edge label={#1}}
}, % make the mark an entry of the \mmat matrix
pmark/.code n args={2}{%
\pgfmathtruncatemacro{\myi}{int({\mmat}[\numexpr#1][\numexpr#2])}%
\tikzset{suppress if 0=\myi,edge label={$\myi$},
amark}% <- changed
},
terminal/.style 2 args={draw,alias=ln,circle,inner sep=2pt,label={#1:#2}},
% semicircle path
semicircle/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.north) arc[start angle=180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.south) arc[start angle=0,end angle=-180,radius=-0.5*\x1]
\fi
\tikztonodes}},
semicircle'/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.south) arc[start angle=-180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.north) arc[start angle=0,end angle=180,radius=-0.5*\x1]
\fi
\tikztonodes}},
add key if/.code n args={3}{\pgfmathtruncatemacro{\itest}{(#1?0:1)}%
\ifcase\itest
\tikzset{#2}%
\else
\tikzset{#3}%
\fi
},suppress if 0/.style={add key if={#1==0}{opacity=0}{}}
]
\pgfmathtruncatemacro{\dimy}{dim({\mmat})} % number of rows
\pgfmathtruncatemacro{\dimx}{dim({\mmat}[0])} % number of columns
\typeout{\dimy,\dimx}
% create the graph
\path % R node
node[terminal={left}{$R(S)$},alias={X-\dimy}] (R) {}
% loop over matrix entries
foreach \Y [evaluate=\Y as \X using {int(\dimy-\Y)}]
in {1,...,\numexpr\dimy-1}
{node[right=of ln,terminal={below right}{% sX_i node
$sX_{\X}(s)$}](sX-\X){}
node[right=of ln,terminal={below right}{% X_i node
$X_{\X}(s)$}](X-\X){}
% ege from sX_i to X_i
(sX-\X) edge[amark,edge label={$\frac{1}{s}$}] (X-\X)
% edge from X_{i+1} to X_i (R had an alias)
(X-\the\numexpr\X+1) edge[pmark={\X-1}{\X}] (sX-\X)
% semicircle edge from X_i to sX_i
(X-\X) edge[semicircle,pmark={\X-1}{\X-1}] (sX-\X)
}
node[right=of ln,terminal={right}{$Y(s)$},alias=sX-\dimy](Y){}
(X-1) edge[pmark={\dimy-1}{0}] (Y)
% we are now done with the horizontal part,
% and have also dealt with the entries on the diagonal and
% the {i-1},i entries
% now we deal with the matrix entries
foreach \X in {1,...,\the\numexpr\dimx-1}
{% all edges that end in Y (excluding the horizontal one)
\ifnum\X>\numexpr1\relax
(X-\X) edge[pmark={\dimx-1}{\X-1},semicircle] (Y)
\fi
% all edges that start at R (excluding the horizontal one)
\ifnum\X<\numexpr\dimx-1\relax
(R) edge[pmark={\X-1}{\dimx-1},semicircle] (sX-\X)
\fi
% remaining semicircles
foreach \Y in {\the\numexpr\X+1,...,\dimy}
{% backwards pointing semicircles
\unless\ifnum\X\Y=1\dimy
(X-\X) edge[pmark={\Y-1}{\X-1},semicircle] (sX-\Y)
\fi
% forward pointing semicircles
\pgfextra{\pgfmathtruncatemacro{\itest}{(\Y<\dimy&&\Y-\X>1?1:0)}}
\ifnum\itest=\numexpr1\relax
(X-\Y) edge[swap,pmark={\X-1}{\Y-1},semicircle'] (sX-\X)
\fi
}
};
\end{tikzpicture}
\end{document}
```