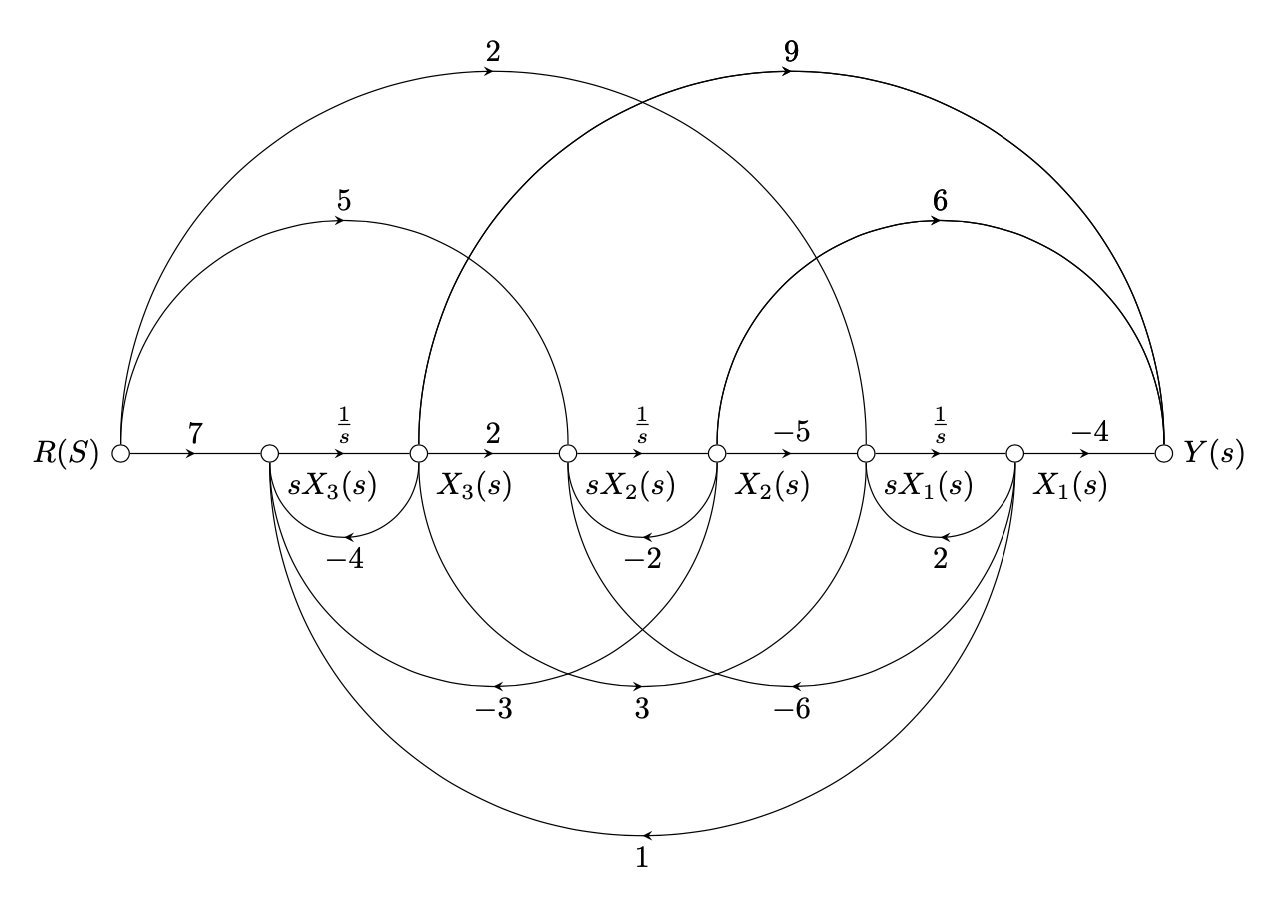
This is an attempt to disentangle the cases more clearly, and make it easier to customize the code. In particular, there are various comments in the code.
* These comments may or may not use intuitive wording, so an alternative way to see what different pieces do is to just add a key like `red` to a given edge, then one sees which edges are controlled by this piece of code.
* Something freaky is going on (I meant to report it already in my previous answer). Sometimes the `\ifnum`s go berserk. I thought I had already some intuition when one could use them without problems, and would have thought that this was such a case. However, for some reason now some of them only work when one adds a `\numexpr` after the `=`, `>` or `<` operator. *Maybe* a kernel change is responsible for that. So if on TeX.SE some complaints surface that some old codes by some deleted users seem not to work, please let me know, this may give further credit to the suggestion that some kernel change is to blame. It may also be that I was too optimistic when using the `\ifnum`s here (but in this case why would adding `\numexpr` "repair" them?). Anyway, if you are wondering why there are all these useless `\numexpr`, on my LaTeX installation they seem to be necessary.
* I did away with the `label revd` stuff. IMHO there is no reason to prefer it to a good old `edge` label, which one could swap.
* I also added a `semicircle'` which is drawn on the opposite site of a `semicircle`.
So this is the result of the exercise.
```
\edef\mmat{%
{2,-5,3,2},%
{-6,-2,2,5},%
{1,-3,-4,7},%
{-4,6,9,0}%
}
\documentclass[tikz,border=5mm]{standalone}
\usetikzlibrary{calc,decorations.markings,positioning,arrows.meta}
\begin{document}
\begin{tikzpicture}[node distance = 15 mm,
amark/.style={
decoration={
markings,
mark=at position {0.5} with {
\arrow{stealth},
}
},
postaction={decorate,edge label={#1}}
}, % make the mark an entry of the \mmat matrix
pmark/.code n args={2}{%
\pgfmathtruncatemacro{\myi}{int({\mmat}[\numexpr#1][\numexpr#2])}%
\tikzset{suppress if 0=\myi,edge label={$\myi$},
amark}% <- changed
},
terminal/.style 2 args={draw,alias=ln,circle,inner sep=2pt,label={#1:#2}},
% semicircle path
semicircle/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.north) arc[start angle=180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.south) arc[start angle=0,end angle=-180,radius=-0.5*\x1]
\fi
\tikztonodes}},
semicircle'/.style={to path={let \p1=($(\tikztotarget)-(\tikztostart)$)
in \ifdim\x1>0pt
(\tikztostart.south) arc[start angle=-180,end angle=0,radius=0.5*\x1]
\else
(\tikztostart.north) arc[start angle=0,end angle=180,radius=-0.5*\x1]
\fi
\tikztonodes}},
add key if/.code n args={3}{\pgfmathtruncatemacro{\itest}{(#1?0:1)}%
\ifcase\itest
\tikzset{#2}%
\else
\tikzset{#3}%
\fi
},suppress if 0/.style={add key if={#1==0}{opacity=0}{}}
]
\pgfmathtruncatemacro{\dimy}{dim({\mmat})} % number of rows
\pgfmathtruncatemacro{\dimx}{dim({\mmat}[0])} % number of columns
% create the graph
\path % R node
node[terminal={left}{$R(S)$},alias={X-\dimy}] (R) {}
% loop over matrix entries
foreach \Y [evaluate=\Y as \X using {int(\dimy-\Y)}]
in {1,...,\numexpr\dimy-1}
{node[right=of ln,terminal={below right}{% sX_i node
$sX_{\X}(s)$}](sX-\X){}
node[right=of ln,terminal={below right}{% X_i node
$X_{\X}(s)$}](X-\X){}
% ege from sX_i to X_i
(sX-\X) edge[amark,edge label={$\frac{1}{s}$}] (X-\X)
% edge from X_{i+1} to X_i (R had an alias)
(X-\the\numexpr\X+1) edge[pmark={\X-1}{\X}] (sX-\X)
% semicircle edge from X_i to sX_i
(X-\X) edge[semicircle,pmark={\X-1}{\X-1}] (sX-\X)
}
node[right=of ln,terminal={right}{$Y(s)$},alias=sX-\dimy](Y){}
(X-1) edge[pmark={\dimy-1}{0}] (Y)
% we are now done with the horizontal part,
% and have also dealt with the entries on the diagonal and
% the {i-1},i entries
% now we deal with the matrix entries
foreach \X in {1,...,\the\numexpr\dimx-1}
{% all edges that end in Y (excluding the horizontal one)
\ifnum\X>\numexpr1\relax
(X-\X) edge[pmark={\dimx-1}{\X-1},semicircle] (Y)
\fi
% all edges that start at R (excluding the horizontal one)
\ifnum\X<\numexpr\dimx-1\relax
(R) edge[pmark={\X-1}{\dimx-1},semicircle] (sX-\X)
\fi
% remaining semicircles
foreach \Y in {\the\numexpr\X+1,...,\dimy}
{% backwards pointing semicircles
\unless\ifnum\X\Y=1\dimy
(X-\X) edge[pmark={\Y-1}{\X-1},semicircle] (sX-\Y)
\fi
% forward pointing semicircles
\pgfextra{\pgfmathtruncatemacro{\itest}{(\Y<\dimy&&\Y-\X>1?1:0)}}
\ifnum\itest=\numexpr1\relax
(X-\Y) edge[swap,pmark={\X-1}{\Y-1},semicircle'] (sX-\X)
\fi
}
};
\end{tikzpicture}
\end{document}
```