How can one draw a circle on the sphere with center P inside a sphere and normal n distinguishing hidden and visible stretches?
tikz add tag
Anonymous 1123 
Based on the answer [here](https://topanswers.xyz/tex?q=1537), now I tried with all the points have integer coordinates inside the sphere `x^2+y^2+z^2=25` (except center of sphere)
I tried
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot-circleofsphere}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\usetikzlibrary{decorations.pathreplacing}%
\begin{document}
	\tdplotsetmaincoords{60}{110}
	\foreach \mytestT in {(-4, -2, -2), (-4, -2, -1), (-4, -2, 0), (-4, -2, 1), (-4, -2, 2), (-4, -1, -2), (-4, -1, -1), (-4, -1, 0), (-4, -1, 1), (-4, -1, 2), (-4, 0, -2), (-4, 0, -1), (-4, 0, 0), (-4, 0, 1), (-4, 0, 2), (-4, 1, -2), (-4, 1, -1), (-4, 1, 0), (-4, 1, 1), (-4, 1, 2), (-4, 2, -2), (-4, 2, -1), (-4, 2, 0), (-4, 2, 1), (-4, 2, 2), (-3, -3, -2), (-3, -3, -1), (-3, -3, 0), (-3, -3, 1), (-3, -3, 2), (-3, -2, -3), (-3, -2, -2), (-3, -2, -1), (-3, -2, 0), (-3, -2, 1), (-3, -2, 2), (-3, -2, 3), (-3, -1, -3), (-3, -1, -2), (-3, -1, -1), (-3, -1, 0), (-3, 	-1, 1), (-3, -1, 2), (-3, -1, 3), (-3, 0, -3), (-3, 0, -2), (-3, 0, -1), (-3, 0, 0), (-3, 0, 1), (-3, 0, 2), (-3, 0, 3), (-3, 1, -3), (-3, 1, -2), (-3, 1, -1), (-3, 1, 0), (-3, 1, 1), (-3, 1, 2), (-3, 1, 3), (-3, 2, -3), (-3, 2, -2), (-3, 2, -1), (-3, 2, 0), (-3, 2, 1), (-3, 2, 2), (-3, 2, 3), (-3, 3, -2), (-3, 3, -1), (-3, 3, 0), (-3, 3, 1), (-3, 3, 2), (-2, -4, -2), (-2, -4, -1), (-2, -4, 0), (-2, -4, 1), (-2, -4, 2), (-2, -3, -3), (-2, -3, -2), (-2, -3, -1), (-2, -3, 0), (-2, -3, 1), (-2, -3, 2), (-2, -3, 3), (-2, -2, -4), (-2, -2, -3), (-2, -2, -2), (-2, -2, -1), (-2, -2, 0), (-2, -2, 1), (-2, -2, 2), (-2, -2, 3), (-2, -2, 4), (-2, -1, -4), (-2, -1, -3), (-2, -1, -2), (-2, -1, -1), (-2, -1, 0), (-2, -1, 1), (-2, -1, 2), (-2, -1, 3), (-2, -1, 4), (-2, 0, -4), (-2, 0, -3), (-2, 0, -2), (-2, 0, -1), (-2,	0, 0), (-2, 0, 1), (-2, 0, 2), (-2, 0, 3), (-2, 0, 4), (-2, 1, -4), (-2, 1, -3), (-2, 1, -2), (-2, 1, -1), (-2, 1, 0), (-2, 1, 1), (-2, 1, 2), (-2, 1, 3), (-2, 1, 4), (-2, 2, -4), (-2, 2, -3), (-2, 2, -2), (-2, 2, -1), (-2, 2, 0), (-2, 2, 1), (-2, 2, 2), (-2, 2, 3), (-2, 2, 4), (-2, 3, -3), (-2, 3, -2), (-2, 3, -1), (-2, 3, 0), (-2, 3, 1), (-2, 3, 2), (-2, 3, 3), (-2, 4, -2), (-2, 4, -1), (-2, 4, 0), (-2, 4, 1), (-2, 4, 2), (-1, -4, -2), (-1, -4, -1), (-1, -4, 0), (-1, -4, 1), (-1, -4, 2), (-1, -3, -3), (-1, -3, -2), (-1, -3, -1), (-1, -3, 0), (-1, -3, 1), (-1, -3, 2), (-1, -3, 3), (-1, -2, -4), (-1, -2, -3), (-1, -2, -2), (-1, -2, -1), (-1, -2, 0), (-1, -2, 1), (-1, -2, 2), (-1, -2, 3), (-1, -2, 4), (-1, -1, -4), (-1, -1, -3), (-1, -1, -2), (-1, -1, -1), (-1, -1, 0), (-1, -1, 1), (-1, -1, 2), (-1, -1, 3), (-1, -1, 4), (-1, 0, -4), (-1, 0, -3), (-1, 0, -2), (-1, 0, -1), (-1, 0, 0), (-1, 0, 1), (-1, 0, 2), (-1, 0, 3), (-1, 0, 4), (-1, 1, -4), (-1, 1, -3), (-1, 1, -2), (-1, 1, -1), (-1, 1, 0), (-1, 1, 1), (-1, 1, 2), (-1, 1, 3), (-1, 1, 4), (-1, 2, -4), (-1, 2, -3), (-1, 2, -2), (-1, 2, -1), (-1, 2, 0), (-1, 2, 1), (-1, 2, 2), (-1, 2, 3), (-1, 2, 4), (-1, 3, -3), (-1, 3, -2), (-1, 3, -1), (-1, 3, 0), (-1, 3, 1), (-1, 3, 2), (-1, 3, 3), (-1, 4, -2), (-1, 4, -1), (-1, 4, 0), (-1, 4, 1), (-1, 4, 2), (0, -4, -2), (0, -4, -1), (0, -4, 0), (0, -4, 1), (0, -4, 2), (0, -3, -3), (0, -3, -2), (0, -3, -1), (0, -3, 0), (0, -3, 1), (0, -3, 2), (0, -3, 3), (0, -2, -4), (0, -2, -3), (0, -2, -2), (0, -2, -1), (0, -2, 0), (0, -2, 1), (0, -2, 2), (0, -2, 3), (0, -2, 4), (0, -1, -4), (0, -1, -3), (0, -1, -2), (0, -1, -1), (0, -1, 0), (0, -1, 1), (0, -1, 2), (0, -1, 3), (0, -1, 4), (0, 0, -4), (0, 0, -3), (0, 0, -2), (0, 0, -1), (0, 0, 1), (0, 0, 2), (0, 0, 3), (0, 0, 4), (0, 1, -4), (0, 1, -3), (0, 1, -2), (0, 1, -1), (0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 1, 3), (0, 1, 4), (0, 2, -4), (0, 2, -3), (0, 2, -2), (0, 2, -1), (0, 2, 0), (0, 2, 1), (0, 2, 2), (0, 2, 3), (0, 2, 4), (0, 3, -3), (0, 3, -2), (0, 3, -1), (0, 3, 0), (0, 3, 1), (0, 3, 2), (0, 3, 3), (0, 4, -2), (0, 4, -1), (0, 4, 0), (0, 4, 1), (0, 4, 2), (1, -4, -2), (1, -4, -1), (1, -4, 0), (1, -4, 1), (1, -4, 2), (1, -3, -3), (1, -3, -2), (1, -3, -1), (1, -3, 0), (1, -3, 1), (1, -3, 2), (1, -3, 3), (1, -2, -4), (1, -2, -3), (1, -2, -2), (1, -2, -1), (1, -2, 0), (1, -2, 1), (1, -2, 2), (1, -2, 3), (1, -2, 4), (1, -1, -4), (1, -1, -3), (1, -1, -2), (1, -1, -1), (1, -1, 0), (1, -1, 1), (1, -1, 2), (1, -1, 3), (1, -1, 4), (1, 0, -4), (1, 0, -3), (1, 0, -2), (1, 0, -1), (1, 0, 0), (1, 0, 1), (1, 0, 2), (1, 0, 3), (1, 0, 4), (1, 1, -4), (1, 1, -3), (1, 1, -2), (1, 1, -1), (1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 1, 4), (1, 2, -4), (1, 2, -3), (1, 2, -2), (1, 2, -1), (1, 2, 0), (1, 2, 1), (1, 2, 2), (1, 2, 3), (1, 2, 4), (1, 3, -3), (1, 3, -2), (1, 3, -1), (1, 3, 0), (1, 3, 1), (1, 3, 2), (1, 3, 3), (1, 4, -2), (1, 4, -1), (1, 4, 0), (1, 4, 1), (1, 4, 2), (2, -4, -2), (2, -4, -1), (2, -4, 0), (2, -4, 1), (2, -4, 2), (2, -3, -3), (2, -3, -2), (2, -3, -1), (2, -3, 0), (2, -3, 1), (2, -3, 2), (2, -3, 3), (2, -2, -4), (2, -2, -3), (2, -2, -2), (2, -2, -1), (2, -2, 0), (2, -2, 1), (2, -2, 2), (2, -2, 3), (2, -2, 4), (2, -1, -4), (2, -1, -3), (2, -1, -2), (2, -1, -1), (2, -1, 0), (2, -1, 1), (2, -1, 2), (2, -1, 3), (2, -1, 4), (2, 0, -4), (2, 0, -3), (2, 0, -2), (2, 0, -1), (2, 0, 0), (2, 0, 1), (2, 0, 2), (2, 0, 3), (2, 0, 4), (2, 1, -4), (2, 1, -3), (2, 1, -2), (2, 1, -1), (2, 1, 0), (2, 1, 1), (2, 1, 2), (2, 1, 3), (2, 1, 4), (2, 2, -4), (2, 2, -3), (2, 2, -2), (2, 2, -1), (2, 2, 0), (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 2, 4), (2, 3, -3), (2, 3, -2), (2, 3, -1), (2, 3, 0), (2, 3, 1), (2, 3, 2), (2, 3, 3), (2, 4, -2), (2, 4, -1), (2, 4, 0), (2, 4, 1), (2, 4, 2), (3, -3, -2), (3, -3, -1), (3, -3, 0), (3, -3, 1), (3, -3, 2), (3, -2, -3), (3, -2, -2), (3, -2, -1), (3, -2, 0), (3, -2, 1), (3, -2, 2), (3, -2, 3), (3, -1, -3), (3, -1, -2), (3, -1, -1), (3, -1, 0), (3, -1, 1), (3, -1, 2), (3, -1, 3), (3, 0, -3), (3, 0, -2), (3, 0, -1), (3, 0, 0), (3, 0, 1), (3, 0, 2), (3, 0, 3), (3, 1, -3), (3, 1, -2), (3, 1, -1), (3, 1, 0), (3, 1, 1), (3, 1, 2), (3, 1, 3), (3, 2, -3), (3, 2, -2), (3, 2, -1), (3, 2, 0), (3, 2, 1), (3, 2, 2), (3, 2, 3), (3, 3, -2), (3, 3, -1), (3, 3, 0), (3, 3, 1), (3, 3, 2), (4, -2, -2), (4, -2, -1), (4, -2, 0), (4, -2, 1), (4, -2, 2), (4, -1, -2), (4, -1, -1), (4, -1, 0), (4, -1, 1), (4, -1, 2), (4, 0, -2), (4, 0, -1), (4, 0, 0), (4, 0, 1), (4, 0, 2), (4, 1, -2), (4, 1, -1), (4, 1, 0), (4, 1, 1), (4, 1, 2), (4, 2, -2), (4, 2, -1), (4, 2, 0), (4, 2, 1), (4, 2, 2)}
	{\begin{tikzpicture}[tdplot_main_coords,line join = round, 
			line cap = round, declare function={R=5;D=7;}]
			\path \mytestT\space  coordinate (T)  %center of circle defined by the intersection
			(0,0,0) coordinate (I); 
			\path [3d coordinate={(myn)=(T)-(I)}];
			\pgfmathsetmacro{\myn}{TD("(myn)")}
			\pgfmathsetmacro{\myd}{sqrt(TD("(myn)o(myn)"))}
			\ifdim\myd pt<0.1pt
			\typeout{The distance between the center of the sphere and the center of the
				circle is too small. Cannot determine a unique plane.}
			\else	 
			\pgfmathsetmacro{\mynn}{1/\myd}
			\pgfmathsetmacro{\myez}{TD("\mynn*(\myn)")}
			\pgfmathsetmacro{\myex}{normalcandidate(\myez)}
			\pgfmathsetmacro{\myey}{TD("(\myez)x(\myex)")}
			\path (\myex) coordinate (ex) (\myey) coordinate (ey) (\myez) coordinate (ez);
			\begin{scope}[x={(ex)},y={(ey)},z={(ez)},canvas is xy plane at z=0,shift={(T)}]
				\path (D,D) coordinate (p1) (D,-D) coordinate (p2)
				(-D,-D) coordinate (p3) (-D,D) coordinate (p4);
			\end{scope}
			\pgfmathsetmacro{\mysd}{screendepth(\myn)}
			\pgfmathsetmacro{\myr}{sqrt(R*R-\myd*\myd)}
			\pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")}
			\pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]}
			\pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]}
			\pgfmathsetmacro{\mygamma}{sign(\mysd)*asin(\myd/R)}
			\tdplotCsDrawCircle[tdplotCsFront/.style={draw=none},
			tdplotCsBack/.style={draw=none}]{R}{\myalpha}{\mybeta}{\mygamma}		   
			\pgfmathsetmacro{\mydtest}{veclen(x2d("coffs")-x2d("T"),y2d("coffs")-y2d("T"))}
			\ifdim\mydtest pt>2pt
			\pgfmathsetmacro{\mygamma}{-1*\mygamma}
			\fi
			\tikzset{stored path/reset coordinate index}
			\tdplotCsDrawCircle[tdplotCsFront/.style={store path=fore},
			tdplotCsBack/.style={draw,dashed}]{R}{\myalpha}{\mybeta}{\mygamma}		   
			\begin{scope}[tdplot_screen_coords]
				% only for animation
				\path (-R-D,-R-D) rectangle (R+D,R+D);	
				\tikzset{draw sphere/.code={\shade[ball color=white,opacity=0.8] (I) circle[radius=R];},
					draw rest/.code={
						\ifnum\np>0
						\path [stored path/first coordinate of=fore] coordinate (aux-0)
						[stored path/last coordinate of=fore]  coordinate (aux-1);
						\begin{scope} 
							\clip (p1) -- (p2) -- (p3) -- (p4) -- cycle;
							\fill[opacity=0.3,blue,even odd rule] 
							(p1) -- (p2) -- (p3) -- (p4) -- cycle
							let \p0=(aux-0),\p1=(aux-1),\n0={atan2(\y0,\x0)},
							\n1={atan2(\y1,\x1)+(\iorder>0?0:360)}
							in	[stored path/restore path=fore] 
							arc[start angle=\n1,end angle=\n0,radius=R]
							-- cycle;
						\end{scope}	
						\draw[stored path/restore path=fore];
						\else
						\fill[opacity=0.3,blue,even odd rule] 
						(p1) -- (p2) -- (p3) -- (p4) -- cycle;
						\fi 
				}}
				\pgfmathtruncatemacro{\np}{tikztdindexoflastcoordinate}
				\pgfmathtruncatemacro{\iorder}{sign(\mysd)}
				\ifnum\iorder=1
				\tikzset{draw sphere,draw rest}      	
				\else
				\tikzset{draw rest,draw sphere}      	
				\fi 
			\end{scope}	
			\fi
	\end{tikzpicture}}
\end{document}
```
I get the massage 
![ScreenHunter 983.png](/image?hash=df2306e163c7418b6a5fc27fd9f6a63395ccaa662b67c95e4ceee376a2da8b91)
I think, if I remove the ractangle, massage will also remove. 
Given a sphere of radius R around a center C, a point P inside the sphere, and a normal vector n, how can one draw a circle on the sphere with center P and normal n distinguishing hidden and visible stretches.
Top Answer
user 3.14159 
Here is a `3dtools` method to draw an arbitrary circle on the sphere. (At the moment it does not yet work if the centers of the circle and the sphere coincide because in this case we need to also specify a normal.) Perhaps more important than the routine is the derivation of how to discern points in the foreground from background points without resorting to a specifi convention for the views.
```
\documentclass{article}
\usepackage[margin=1in]{geometry}
\usepackage{amsmath}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{angles,3dtools}% https://github.com/marmotghost/tikz-3dtools
\DeclareMathOperator{\sd}{sd}
\begin{document}
We are given a sphere around a center $C$ or radius $R$ and a point $P$ inside
the sphere. If $C$ and $P$ coincide, we need to define a normal $n$, otherwise
$n=P-C$.  How can one draw a circle on the sphere, distinguishing between
visible and hidden stretches?

\paragraph{\boldmath First test: $|P-C|<R$.} The circle only makes sense if
$|P-C|<R$. The radius of the circle is $r=\sqrt{R^2-|P-C|^2}$. Call the normal
on the screen $n_\mathrm{screen}$. 

\paragraph{\boldmath Case $n\parallel n_\mathrm{screen}$.} If $n$ and $n_\mathrm{screen}$ are linearly dependent, the circle is completely
hidden if the screen depth of $P$ is smaller than the screen depth of $C$, $\sd
P <\sd$, and visible otherwise. We can choose a coordinate system in which 
\[ e_z=\frac{n}{|n|}\;,\quad e_x\text{ arbitary but }\perp e_z
\quad\text{and}\quad e_y=e_z\times e_x\]
to draw the circle.

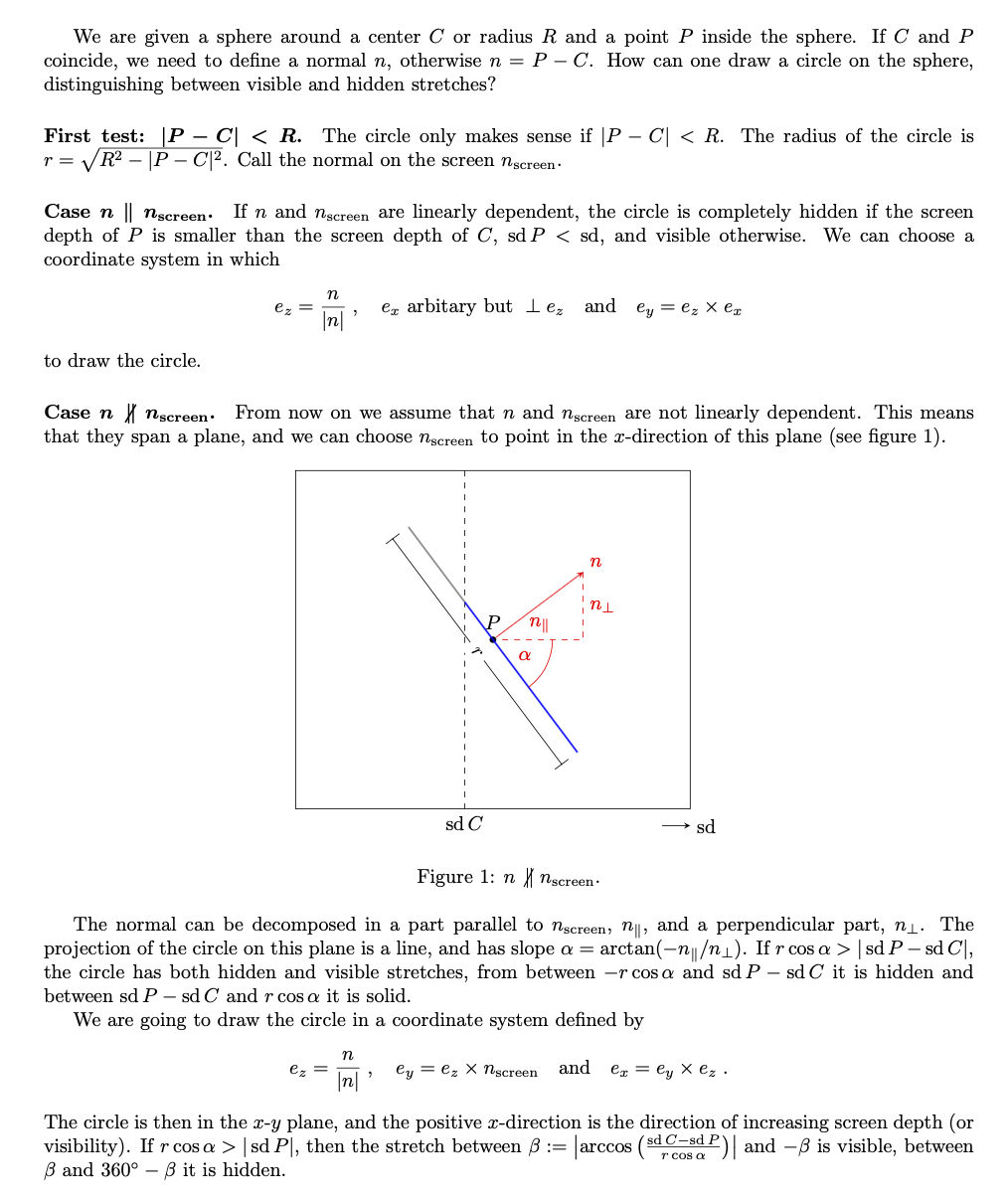
\paragraph{\boldmath Case $n\not\,\parallel n_\mathrm{screen}$.} From now on we assume that $n$ and $n_\mathrm{screen}$ are not linearly
dependent. This means that they span a plane, and we can choose
$n_\mathrm{screen}$ to point in the $x$-direction of this plane (see
figure~\ref{fig:not_parallel}).

\begin{figure}[htb]
\centering
\begin{tikzpicture}
 \draw (-3,-3) rectangle (4,3);
 \draw[dashed] (0,3) coordinate (t) -- (0,-3) coordinate (b)node[below]{$\sd C$};
 \draw[-stealth] (3.5,-3.3) -- (4,-3.3) node[right] {$\sd$};
 \path (2,-2) coordinate (c1) -- (-1,2) coordinate (c2)
 	node[midway,circle,fill,inner sep=1.2pt,label=above:{$P$}](P){};
 \draw[thick,blue] (intersection of c1--c2 and t--b) coordinate (i) -- coordinate (v) (c1) ;	
 \draw[thick,gray] (i) -- coordinate (h) (c2) ;	
 \draw ($(c1)!5mm!90:(c2)$) --  coordinate (r1) ($(c1)!2mm!90:(c2)$)
 ($(c2)!5mm!-90:(c1)$) --  coordinate (r2) ($(c2)!2mm!-90:(c1)$)
 (r1) -- node[sloped,fill=white]{$r$} (r2);
 \draw[red,-stealth] (P) -- ($(P)!20mm!90:(c1)$)coordinate (n) node[pos=1.15]{$n$};
 \draw[red,dashed] (n) |- (P) node[pos=0.25,right]{$n_\perp$}
  coordinate[pos=0.5] (aux)
  node[pos=0.75,above]{$n_\parallel$}
  pic[draw,solid,pic text={$\alpha$},angle radius=3em,angle eccentricity=0.6]{angle=c1--P--aux};
\end{tikzpicture}
\caption{$n\not\,\parallel n_\mathrm{screen}$.}
\label{fig:not_parallel}
\end{figure}

The normal can be decomposed in a part parallel to $n_\mathrm{screen}$,
$n_\parallel$, and a perpendicular part, $n_\perp$. The projection of the circle
on this plane is a line, and has slope $\alpha=\arctan(-n_\parallel/n_\perp)$.
If $r\cos\alpha>|\sd P-\sd C|$, the circle has both hidden and visible
stretches, from between $-r\cos\alpha$ and $\sd P-\sd C$ it is hidden and between $\sd
P-\sd C$ and $r\cos\alpha$ it is solid. 

We are going to draw the circle in a coordinate system defined by
\[ e_z=\frac{n}{|n|}\;,\quad e_y=e_z\times n_\mathrm{screen}
\quad\text{and}\quad e_x=e_y\times e_z\;.\]
The circle is then in the $x$-$y$ plane, and the positive $x$-direction is the
direction of increasing screen depth (or visibility). If $r\cos\alpha>|\sd P|$,
then the stretch between $\beta:=\left|\arccos\left(\frac{\sd C-\sd
P}{r\cos\alpha}\right)\right|$ and $-\beta$ is visible, between $\beta$ and
$360^\circ-\beta$ it is hidden.
\clearpage

\begin{figure}
\centering
\tdplotsetmaincoords{60}{110}%
\begin{tikzpicture}[tdplot_main_coords,line join = round, 
		line cap = round, declare function={R=5;D=7;}]
  \path (0,0,0) coordinate (C)
 %  (3*0.81381,3*0.2962,3*0.5) coordinate (P)
   (1.5,-1.5,1) coordinate (P);
  \shade[tdplot_screen_coords,ball color=white] (C) circle[radius=R]; 
  \path[overlay,3d coordinate={(n)=(P)-(C)}];
  \pgfmathsetmacro{\ntest}{sqrt(TD("(n)o(n)"))} 
  \ifdim\ntest pt<0.02pt
   % we need a normal
   \typeout{Need to specify a normal.}
  \else
   \pgfmathsetmacro{\ntest}{1/\ntest} 
   \pgfmathsetmacro{\myez}{TD("\ntest*(n)")} 
   \path[overlay] (nscreenx,nscreeny,nscreenz) coordinate (nscreen)
	[3d coordinate/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ez}=(\myez)}];
   %\pgfmathsetmacro{\tmp}{TD("(nscreen)")} 
   %\typeout{\tmp}
   \pgfmathsetmacro{\myd}{tddistance("(P)","(C)")} 
   \pgfmathtruncatemacro{\itest}{(\myd<R?1:0)} 
   \ifnum\itest=0
	\typeout{(P) is not inside the sphere.}
   \else 
	\pgfmathsetmacro{\myey}{TD("\pgfkeysvalueof{/tikz/3d/aux keys/ez}x(nscreen)")}
	\pgfmathsetmacro{\myney}{sqrt(TD("(\myey)o(\myey)"))}
	\pgfmathsetmacro{\myr}{sqrt(R*R-\myd*\myd)}
	\typeout{r=\myr, d=\myd}
	\ifdim\myney pt<0.04pt
     \typeout{(n) is (almost) parallel to normal on screen.}
     \pgfmathsetmacro{\myex}{normalcandidate(\myez)}
     \pgfmathsetmacro{\myey}{TD("(\myez)x(\myex)")}
     \path[overlay] 
      [3d coordinate/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ex}=(\myex)},
	   3d coordinate/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ey}=(\myey)}];
	 \pgfmathtruncatemacro{\jtest}{(TD("\pgfkeysvalueof{/tikz/3d/aux keys/ez}o(n)")<0?0:1)}   
     \begin{scope}[x={(ex)},y={(ey)},z={(ez)},shift={(P)}]
	  \ifcase\jtest
	   % hidden
	   \draw[3d/hidden]  circle[radius=\myr];
	  \or
	   % visible
	   \draw[3d/visible] circle[radius=\myr];
	  \fi
     \end{scope}
	\else 
     \pgfmathsetmacro{\mynpara}{TD("\pgfkeysvalueof{/tikz/3d/aux keys/ez}o(nscreen)")}
     \pgfmathsetmacro{\mynortho}{sqrt(1-\mynpara*\mynpara)}
	 \pgfmathsetmacro{\myalpha}{atan2(-1*\mynpara,\mynortho)}
	 \pgfmathsetmacro{\myP}{TD("(P)")}
	 \pgfmathsetmacro{\sdP}{screendepth(\myP)}
	 \pgfmathsetmacro{\myC}{TD("(C)")}
	 \pgfmathsetmacro{\sdC}{screendepth(\myC)}
	 \pgfmathsetmacro{\myney}{1/\myney}
	 \pgfmathsetmacro{\myey}{TD("\myney*(\myey)")}
	 \pgfmathsetmacro{\myex}{TD("(\myey)x(ez)")}
	 \pgfmathsetmacro{\mynscreen}{TD("(nscreen)")}
	 \path[overlay,
		 3d coordinate/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ex}=(\myex)},
		 3d coordinate/.expanded={\pgfkeysvalueof{/tikz/3d/aux keys/ey}=(\myey)},];
	 \typeout{(ex)=(\myex),(ey)=(\myey), (ez)=(\myez), n_screen=(\mynscreen)}
	 \begin{scope}[x={(ex)},y={(ey)},z={(ez)},shift={(P)}]
	 %
     \pgfmathtruncatemacro{\itest}{(abs(\myr*cos(\myalpha))>abs(\sdP-\sdC)?1:0)} 
     \typeout{npara=\mynpara, northo=\mynortho, alpha=\myalpha, \sdP, \sdC,
	 \itest}
	 \ifcase\itest
	  % only visible or only hidden
	  \pgfmathtruncatemacro{\jtest}{(\sdP<\sdC?0:1)} 
	  \ifcase\jtest
	   % hidden
	   \draw[3d/hidden]  circle[radius=\myr];
	  \or
	   % visible
	   \draw[3d/visible] circle[radius=\myr];
	  \fi
	 \or
	  % mixed
	  \pgfmathsetmacro{\mybeta}{abs(acos((\sdC-\sdP)/\myr*cos(\myalpha)))}
	  \draw[3d/hidden]  (\mybeta:\myr) arc[start angle=\mybeta,
	 	 end angle=360-\mybeta,radius=\myr];
	  \draw[3d/visible]  (\mybeta:\myr) arc[start angle=\mybeta,
	 	 end angle=-\mybeta,radius=\myr];
	 \fi
	 \end{scope}
	\fi	
   \fi
  \fi 
  \path foreach \X in {C,P} {(\X) node[circle,inner
  sep=1.2pt,fill,label=above:{$\X$}]{}};
\end{tikzpicture}
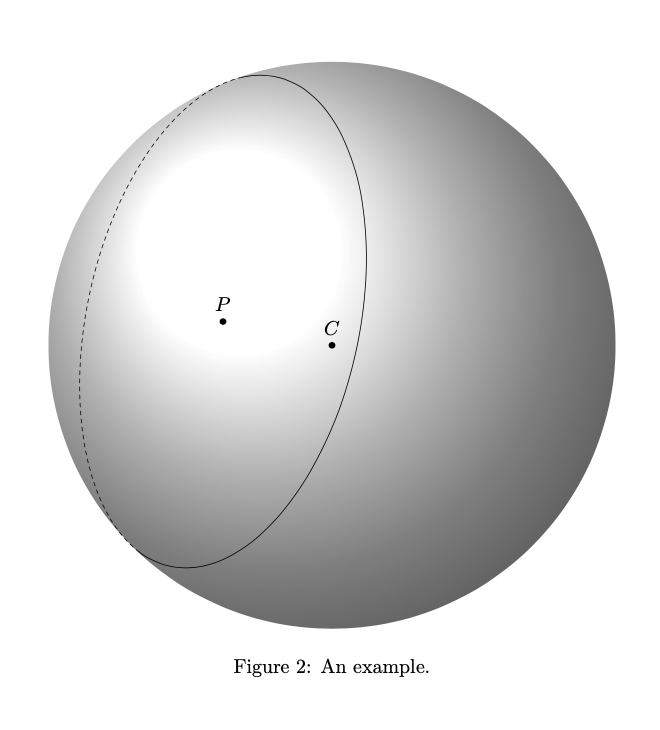
\caption{An example.}
\label{fig:CircleOnSphere}
\end{figure}

\end{document}
```
![Screen Shot 2020-12-05 at 12.24.04 AM.png](/image?hash=45dbd64f3ec8d2dbea7be98d437f009ca2a4b783fe1476f8c0282cbbfdb90aad)
![Screen Shot 2020-12-05 at 12.24.50 AM.png](/image?hash=f3f215ed861f0d4acbb5c18d2d1596c81308e85cd176972bea7d49c424005a3d)

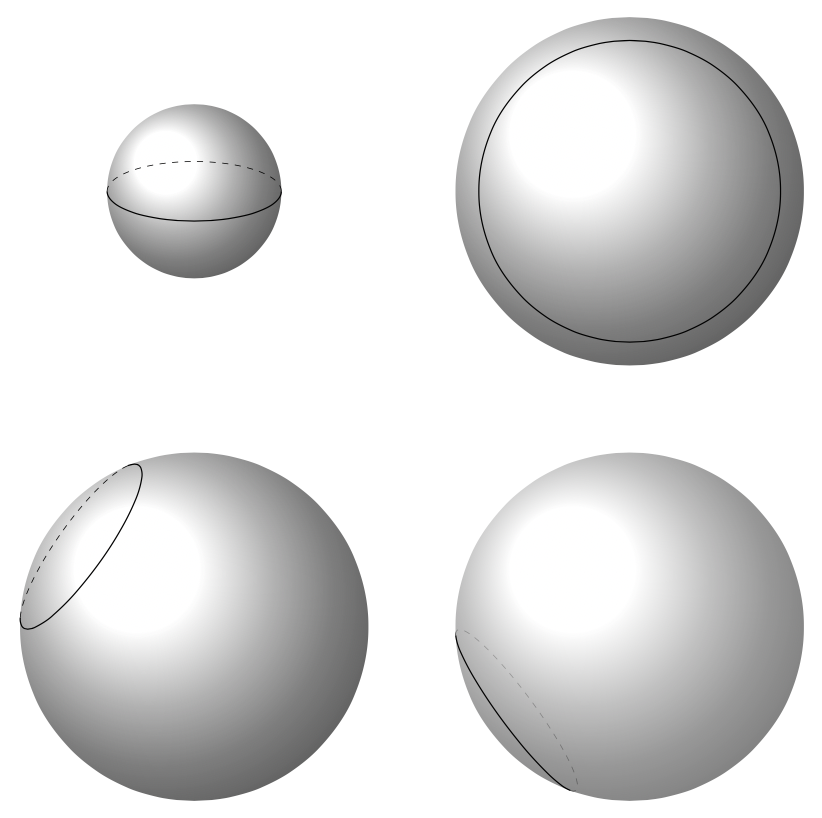
These considerations have lead to yet another pic in the [3dtools library](https://github.com/marmotghost/tikz-3dtools). I hope not to have missed too many special cases. For instance, if `P` happens to be outside the sphere, a warning will be issued. That is, if there is no output, the reason my be given in a message on the console. Of course, there can be mistakes in the package.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\begin{tikzpicture}[3d/install view={phi=110,theta=70}]
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}   
\begin{scope}[declare function={R=1;}] 
 \shade[ball color=white,3d/screen coords] circle[radius=R];
 \path pic{3d/circle on sphere};
\end{scope} 
% 
\begin{scope}[xshift=5cm,declare function={R=2;}] 
 \shade[ball color=white,3d/screen coords] circle[radius=R];
 \path  % (nscreen) gets inherited from the previous scope
 	pic{3d/circle on sphere={R=R,P={(nscreen)}}};
\end{scope} 
% 
\begin{scope}[yshift=-5cm,declare function={R=2;}] 
 \shade[ball color=white,3d/screen coords] circle[radius=R];
 \path  pic{3d/circle on sphere={R=R,P={(0.5,-1.2,1)}}};
\end{scope} 
% 
\begin{scope}[xshift=5cm,yshift=-5cm,declare function={R=2;}] 
 \shade[ball color=white,3d/screen coords,opacity=0.8] circle[radius=R];
 \path  pic{3d/circle on sphere={R=R,P={(0.5,-1.2,-1)},
 	fore layer=foreground,back layer=background}};
\end{scope} 
\end{tikzpicture}
\end{document}
```
![Screen Shot 2020-12-05 at 6.09.54 PM.png](/image?hash=3d31f52284387479a5e9e0b4c888f8e73185471eaf4f582d239bf64d837d8072)
comments
transcript

Enter question or answer id or url (and optionally further answer ids/urls from the same question) from

Separate each id/url with a space. No need to list your own answers; they will be imported automatically.