How to draw intersection of two circles are not in the same plane ? - TeX

TopAnswers TeX

Top Answer

user 3.14159

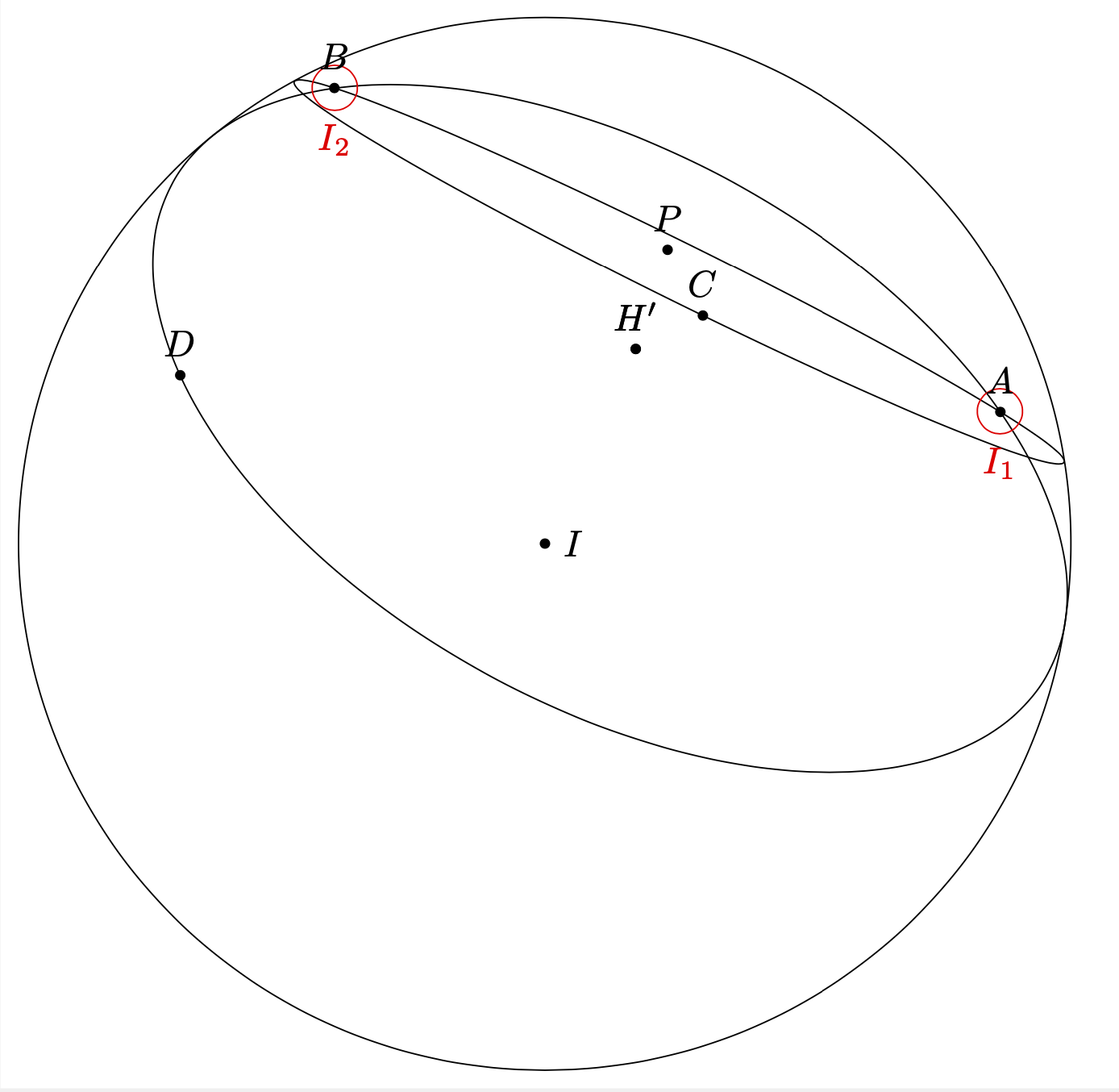
It is very "unlikely" that two circles in 3d intersect in two points. If this happens for two completely specified circles, the system is "overconstrained" in the sense that one can derive the intersections in different ways. The procedure here is
1. Project the center of the first circle, `H` on the plane in which the other circle lies. Call this projection `H'`. 
2. Project the center of the first circle, `K` on the plane in which the other circle lies. Call this projection `K'`.
3. Compute the intersection between the lines `H--K'` and `H'--K`. Generally these lines do not intersect, but if the circles intersect in two points, they do. Call this intersection `P`.
4. The intersections have a distance from `P` which is given by `p=sqrt(r_H^2-d(H,P)^2)`, where `r_H` is the radius of the circle around `H`. It is also given by `sqrt(r_K^2-d(K,P)^2)`, where `r_K` is the radius of the circle aroung `K`.  `d(H,P)` and `d(K,P)` are the distances between `H` and `P`, and `K` and `P`, respectively. This is another manifestation of the statement that the system is "overconstrained".
5. The intersections are `I_i=P\pm p*n`, where `n` is the normal of the plane spanned by `P`, `H` and `K`.

This is the corresponding code. It does not contain cross-checks if the circles really intersect in two points, it just follows the above procedure.
```
\documentclass[border=2mm,tikz]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
	\tdplotsetmaincoords{60}{150}
	\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, 
		line cap = round, declare function={R=5;}]
		\path
		(1,2,3) coordinate (I)
		(-4, 2, 3) coordinate (A)
		(1, -2, 6) coordinate (B)
		(1, 5, 7) coordinate (C) 
		(5,2,6) coordinate (D);
	\path pic{3d circle through 3 points={%
			A={(A)},B={(B)},C={(C)},center name=H}};
    \path pic{3d circle through 3 points={% 
					A={(A)},B={(B)},C={(D)},center name= K}};
    \tikzset{3d/plane through={(A) and (B) and (C) named pABC},
		3d/plane through={(A) and (B) and (D) named pABD}}	
    \path[3d/project={(H) on pABD}] coordinate (H')
	 [3d/project={(K) on pABC}] coordinate (K');						
	\tikzset{3d/line through={(H) and (K') named l1},
		3d/line through={(K) and (H') named l2}} 
	\path[3d/intersection of={l1 with l2}]	coordinate (P);
	\path[overlay,3d coordinate={(n)=(H)-(P)x(K)-(P)}];
	% normalization of n
	\pgfmathsetmacro{\myn}{sqrt(TD("(n)o(n)"))}
	% radius of first circle around H
	\pgfmathsetmacro{\myrA}{sqrt(TD("(A)-(H)o(A)-(H)"))}
	% distance H--P
	\pgfmathsetmacro{\myrB}{sqrt(TD("(P)-(H)o(P)-(H)"))}
	% distance P to intersections
	\pgfmathsetmacro{\myrC}{sqrt(\myrA*\myrA-\myrB*\myrB)}
	% prefactor in linear combinations
	\pgfmathsetmacro{\myp}{\myrC/\myn}
	% build intersections
	\path[overlay,3d coordinate={(I_1)=(P)+\myp*(n)},
		3d coordinate={(I_2)=(P)-\myp*(n)}];
	% mark intersections	
	\path[red] foreach \X in {1,2}
	{(I_\X) node[circle,draw,inner sep=1ex,label=below:{$I_\X$}] {}};	
	%\path [name intersections={of=c1 and c2}];
 
	\begin{scope}[shift={(I)}]
		\draw[tdplot_screen_coords] (I) circle[radius=R]; 
	\end{scope}	
    \path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90,H'/90,H'/90,P/90}
    { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}};
\end{tikzpicture}
\end{document} 
```
![Screen Shot 2020-12-01 at 6.31.08 PM.png](/image?hash=d179f6e3e63941ca3b881888ff3d2b3c0e14ca7f75ed86781f6d12a2af7a6382)

BTW, you could tell the user of [this question](https://tex.stackexchange.com/q/592462) to use ``` \path[name path=e2,bend left=0] (1.5,0,0.8) to (1.5,0,2.6) to (4.5,0,2.6) to (4.5,0,0.8) to cycle; ``` for the second path

Maybe like this? ``` \documentclass[border=2mm,tikz]{standalone} \usetikzlibrary{calc,3dtools} \begin{document} \begin{tikzpicture}[3d/install view=% {phi=150,psi=0,theta=60}, scale=1,line join = round, line cap = round, declare function={R=5;a=7;b=5;c=3; tangle(\a,\b,\c)=acos((\a*\a+\b*\b-\c*\c)/(2*\a*\b));}] \begin{scope}[canvas is xy plane at z=0] \path (0,0) coordinate (B) (c,0) coordinate (C) ({tangle(a,c,b)}:c) coordinate (A) ({-1*tangle(a,c,b)}:c) coordinate (D); \end{scope} \path foreach \p/\g in {B/90,C/90,A/60,D/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \draw (A) -- (B) --(C) --cycle (C) -- (B) --(D) --cycle; \end{tikzpicture} \end{document} ```

Not sure if I am interpreting the question correctly. ``` \documentclass[border=2mm,tikz]{standalone} \usetikzlibrary{intersections,3dtools} \begin{document} \begin{tikzpicture}[3d/install view=% {phi=150,psi=0,theta=60}, scale=1,line join = round, line cap = round, declare function={R=5;}] \path (0,0,0) coordinate (B) (0, 7, 0) coordinate (C) ; \begin{scope}[canvas is xy plane at z=0] \draw[name path=cB] (B) circle[radius=3]; \draw[name path=cC] (C) circle[radius=5]; \path [name intersections={of=cB and cC}]; \coordinate (A) at (intersection-1); \path [name intersections={of=cB and cC}]; \coordinate (D) at (intersection-2); \end{scope} \path foreach \p/\g in {B/90,C/90,A/60,D/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \draw (A) -- (B) --(C) --cycle (C) -- (B) --(D) --cycle; \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1786), How can I repair this code without using `\usepackage{tikz-3dplot}`? ``` \documentclass[border=2mm,tikz]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{intersections} \begin{document} \tdplotsetmaincoords{60}{150} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={R=5;}] \path (0,0,0) coordinate (B) (0, 7, 0) coordinate (C) ; \begin{scope}[canvas is xy plane at z=0] \draw[name path=cB] (B) circle[radius=3]; \draw[name path=cC] (C) circle[radius=5]; \path [name intersections={of=cB and cC}]; \coordinate (A) at (intersection-1); \path [name intersections={of=cB and cC}]; \coordinate (D) at (intersection-2); \end{scope} \path foreach \p/\g in {B/90,C/90,A/60,D/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \draw (A) -- (B) --(C) --cycle (C) -- (B) --(D) --cycle ; \end{tikzpicture} \end{document} ```

I use \usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools \documentclass[border=2mm,tikz]{standalone} \usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools \begin{document} \pgfdeclarelayer{background} \pgfdeclarelayer{foreground} \pgfsetlayers{background,main,foreground} \begin{tikzpicture}[3d/install view={phi=70,theta=80},scale=1,line cap=butt,line join=round,visible/.style={draw,solid},hidden/.style={draw,very thin,cheating dash}, declare function={R=5;h=7;}] \path (-4,2,3)coordinate(A) (1,-2,6)coordinate(B) (1,5,7)coordinate(C) (5,2,5)coordinate(D); \path[3d/circumsphere center={A={(A)},B={(B)},C={(C)},D={(D)}}]coordinate (I); \pgfmathsetmacro{\myR}{sqrt(TD("(I)-(A)o(I)-(A)"))} ; \shade[ball color=white,3d/screen coords,opacity=0.5] (I) circle[radius=\myR]; \draw[3d/screen coords] (I) circle[radius=\myR]; \path[3d/circumcircle center={A={(A)},B={(B)},C={(C)}}] coordinate (H); \path pic{3d/circle on sphere={R=\myR,C={(I)}, P={(H)},fore layer=foreground,back layer=background}}; \path[3d/circumcircle center={A={(A)},B={(B)},C={(D)}}] coordinate (K); \path pic{3d/circle on sphere={R=\myR,C={(I)}, P={(K)},fore layer=foreground,back layer=background}}; \draw[hidden,blue] (A)--(B); \path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90,H/90} { (\p) node[circle,fill=purple,inner sep=.6pt,label=\g:{{$\p$}}]{}}; \end{tikzpicture} \end{document} ![blob](/image?hash=a900bbf506ee688f4362027305db918b1567ab8062b8b94f8a1e5dc259471330)

Well, `tikz-3dplot-circleofsphere` is simple and well-documented, isn't it? (I am sorry, I am not the kind of user who just copies routines from another package. At some point I may potentially adopt them, but also acknowledge the basis of the routines. To see what I mean, type `texdoc mleftright`, say, and compare this to the way Frank Mittelbach reflects on history.)

If you want to send him an email and tell him to look at this site or congratulate him for the package, please go ahead. I have burned my claws when sharing my email with people who I thought were very reasonable, and they were not. All sorts of completely fabricated accusations were made (e.g. that I added a license issue on the `bbox` library which is really absolutely untrue, you can ask e.g. your Vietnamese friend Joule V about this), and have decided not to share my email with anyone. This is not to say that I think that the author of the `tikz-3dplot-circleofsphere` package is not trustworthy, I think he is, but I have learnt my lessons...

Thanks! The research of the author is very interesting! (Cognitive science is actually more fundamental than many would think. I can also understand why he does not have the time and passion to publish the package....) :smile_cat:

1 Answer