How to find intersection point of two circles in any plane? - TeX

TopAnswers TeX

Meta

Databases

TeX

Code Golf

APL

C++

.net

db<>fiddle

Java

*nix

PHP

PowerShell

Python

Rust

टेक्-मराठी

Typst

Web Client Dev

Web Server Dev

How to find intersection point of two circles in any plane?

tikz add tag

Anonymous 1123

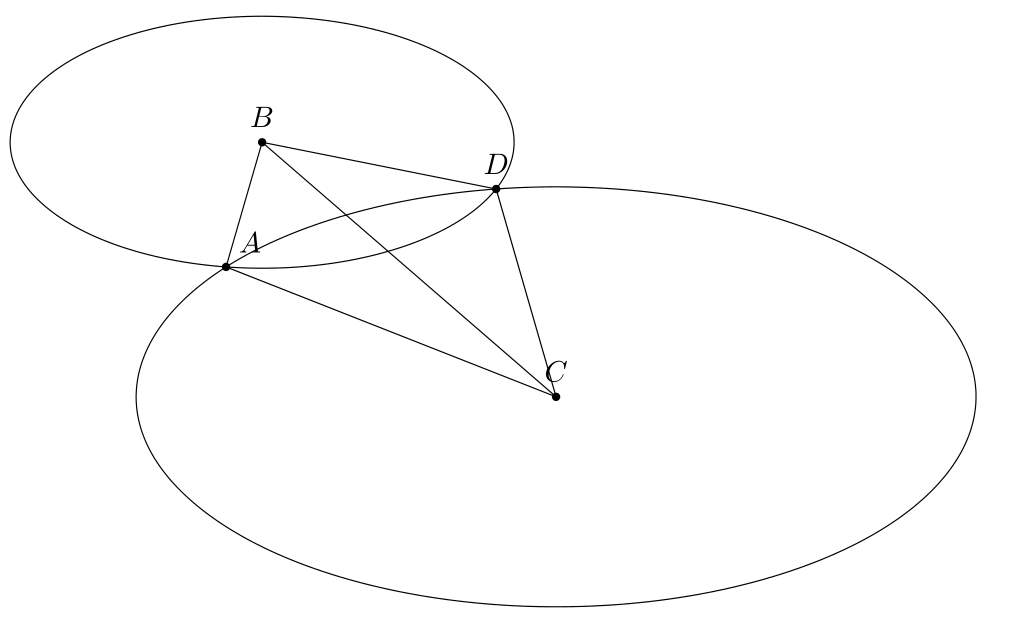
I want to construct triangle with three sides `3, 5, 7` in the `xy` plane. My code
```
\documentclass[border=2mm,tikz]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{intersections}
\begin{document}
	\tdplotsetmaincoords{60}{150}
	\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, 
		line cap = round, declare function={R=5;}]
		\path
		(0,0,0) coordinate (B)
		(0, 7, 0) coordinate (C)
			;
			\begin{scope}[canvas is xy plane at z=0]
			\draw[name path=cB] (B) circle[radius=3];
			\draw[name path=cC] (C) circle[radius=5];
			\path [name intersections={of=cB and cC}];
			\coordinate (A) at (intersection-1);
			\path [name intersections={of=cB and cC}];
			\coordinate (D) at (intersection-2);
			\end{scope}
		\path foreach \p/\g in {B/90,C/90,A/60,D/90}
		{ (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}};
		\draw (A) -- (B) --(C) --cycle
		(C) -- (B) --(D) --cycle
		;
\end{tikzpicture}
\end{document}
```
![ScreenHunter 971.png](/image?hash=d3eb8124876e33aa57fba9a31d2da5c3fb0b5846ab1496284ab1092b75865c10)
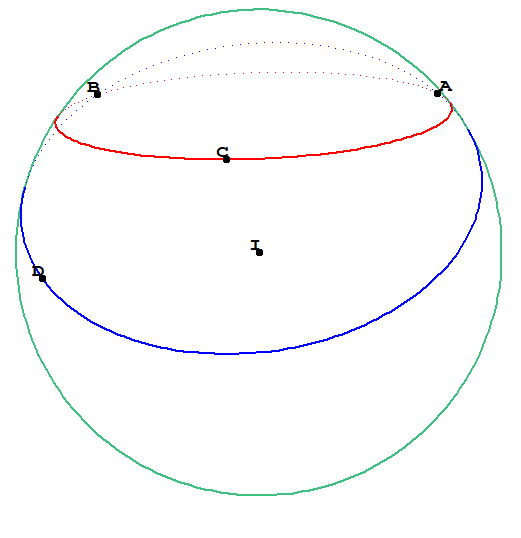
If the plane is not `xy` plane, How to find intersection point of two circles in any plane?

**UPDATE**
Find intersection of two circles `(ABC)` and `(ABD)` where 
```
(-4, 2, 3) coordinate (A)
		(1, -2, 6) coordinate (B)
		(1, 5, 7) coordinate (C) 
		(5,2,6) coordinate (D)
```
This picture is drawn with Geosplan - Geospacw [here](http://www.aid-creem.org/)
![ScreenHunter 973.png](/image?hash=ceabe971728d06f10331d419718ce31df3cf61b6890d19d2dd75965de3f40386)

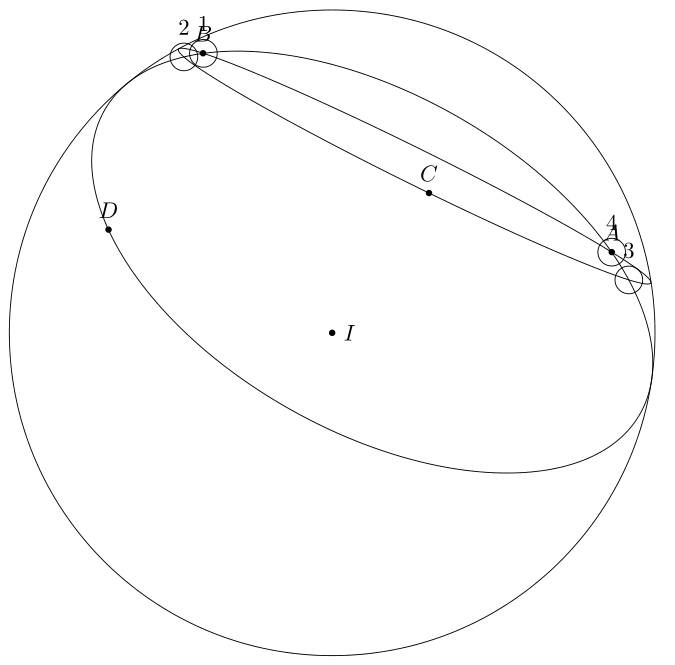
I copied this code from comment
```
\documentclass[border=2mm,tikz]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools,intersections}
\begin{document}
	\tdplotsetmaincoords{60}{150}
	\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, 
		line cap = round, declare function={R=5;}]
		\path
		(1,2,3) coordinate (I)
		(-4, 2, 3) coordinate (A)
		(1, -2, 6) coordinate (B)
		(1, 5, 7) coordinate (C) 
		(5,2,6) coordinate (D)
		;
		\path[every path/.append style={name path global=c1}] pic{3d circle through 3 points={%
				A={(A)},B={(B)},C={(C)},center name=H}};
		\path[every path/.append style={name path global=c2}] pic{3d circle through 3 points={% 
				A={(A)},B={(B)},C={(D)},center name= K}};
		%\path [name intersections={of=c1 and c2}];
		
		\begin{scope}[shift={(I)}]
			\draw[tdplot_screen_coords] (I) circle[radius=R]; 
		\end{scope}	
		\path[name intersections={of=c1 and c2,total=\t}]
		%\pgfextra{\typeout{\t}}
		foreach \X in {1,...,\t}
		{(intersection-\X) node[circle,draw,inner sep=1ex,label=above:$\X$]{}};
		\path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90}
		{ (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}};
	\end{tikzpicture}
\end{document} 
```
I got incorrect result
![ScreenHunter 974.png](/image?hash=63e35a785ae456061cb9cb0a0857a233d959bf503f411d0fed7e3fd9c799b884)

Top Answer

user 3.14159

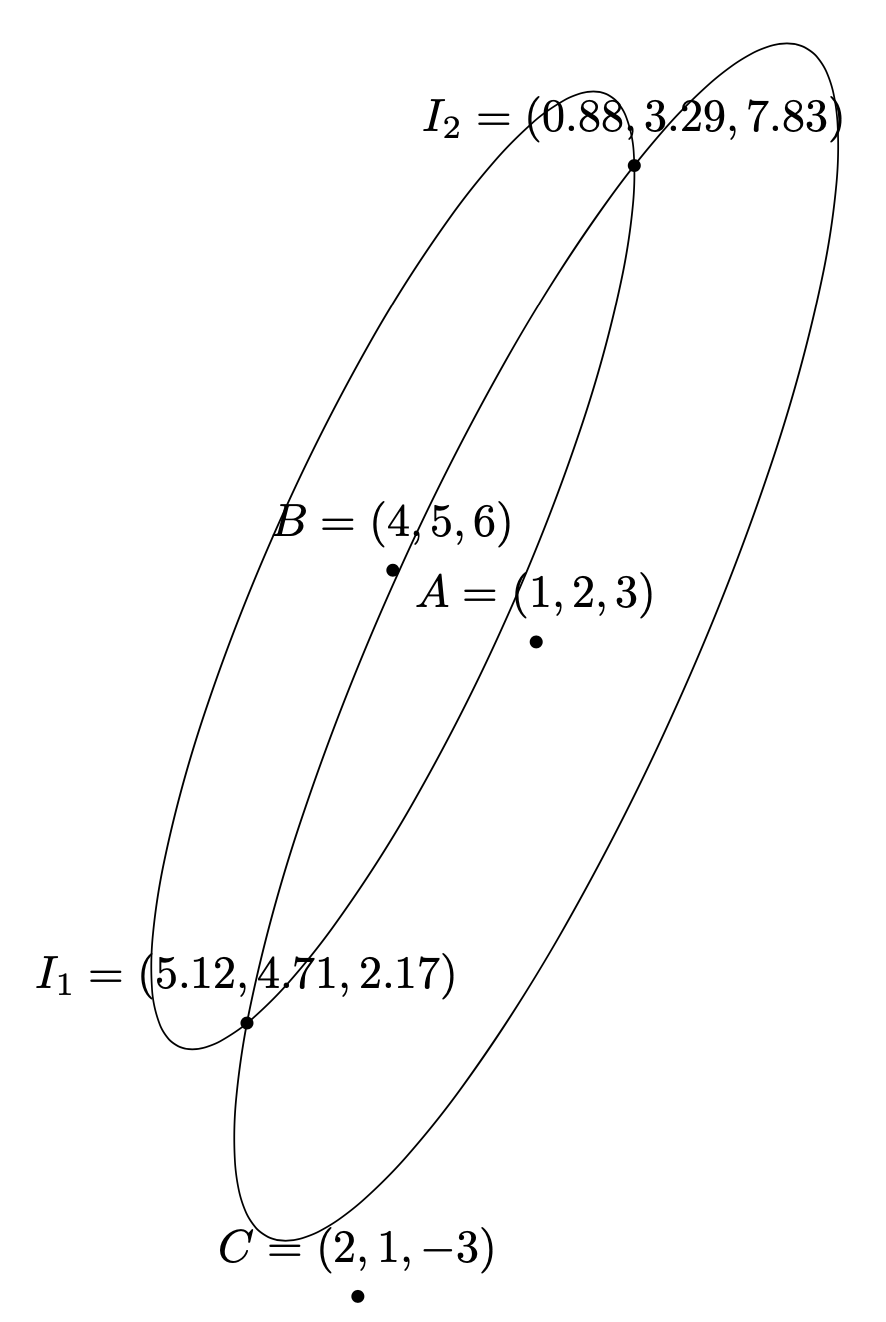
Here is one possible way to answer the question. We are given two points, `A` and `B`, which are the centers of the circles or radii `r1` and `r2`, respectively. A third point `C` which is not collinear with `A--B` defines a plane in three dimensions going through `A`, `B` and `C`. Then there are four cases:
1. The distance `d` between `A` and `B` is larger than the sum of the two radii, i.e. `d>r1+r2`, or `r1>r2+d` or `r2>r1+d`, in which case there is no intersection.
2. `r1+r2=d`, in which case there is a unique intersection.
3. `r1+r2>d` but neither `r1>r2+d` nor `r2>r1+d`. Then there are two intersections.

These cases are covered by the following code.

```
\documentclass[border=2mm,tikz]{standalone}
\usepackage{tikz-3dplot}% https://github.com/marmotghost/tikz-3dtools
\usetikzlibrary{3dtools}
\begin{document}
\tdplotsetmaincoords{60}{150}
\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, 
	line cap = round, declare function={r1=5;r2=4;},
	declare function={cosinelaw(\a,\b,\c)=acos((\a*\a+\b*\b-\c*\c)/(2*\a*\b));}]
	\path (1,2,3) coordinate (A)
	 (4,5,6) coordinate (B)
	 (2,1,-3) coordinate (C);
	 % distance
	 \pgfmathsetmacro{\myd}{sqrt(TD("(A)-(B)o(A)-(B)"))}
	 \ifdim\myd pt<0.2pt\relax
	  \typeout{The two center points are too close to each other.}
	 \else
	  \pgfmathtruncatemacro{\itest}{(\myd+r1<r2?0:1)*(\myd+r2<r1?0:1)*(sign(r1+r2-\myd)+1)}
	  \ifcase\itest
	   \typeout{The circles do not intersect.}
	  \or
	   \typeout{There is one unique intersection.}
	   \pgfmathsetmacro{\myr}{r1/\myd}
	   \path[3d coordinate={(I)=(A)-\myr*(A)+\myr*(B)}];
	  \or
	   \pgfmathsetmacro{\myn}{TD("(A)-(B)x(A)-(C)")} 
	   \pgfmathsetmacro{\myn}{sqrt(TD("(\myn)o(\myn)"))}
	   \ifdim\myn pt<0.1pt\relax
		\typeout{The three points defining the plane are too collinear.}
	   \else
	    \pgfmathsetmacro{\mynx}{1/\myd} 
		\pgfmathsetmacro{\myex}{TD("\mynx*(A)-\mynx*(B)")}
	    \pgfmathsetmacro{\myn}{TD("(A)-(B)x(A)-(C)")} 
		\pgfmathsetmacro{\myey}{TD("(\myex)x(\myn)")}
	    \pgfmathsetmacro{\myny}{1/sqrt(TD("(\myey)o(\myey)"))} 
		\pgfmathsetmacro{\myey}{TD("\myny*(\myey)")}
		\pgfmathsetmacro{\myalpha}{cosinelaw(r1,\myd,r2)}
		\pgfmathsetmacro{\mya}{-r1*cos(\myalpha)}
		\pgfmathsetmacro{\myb}{r1*sin(\myalpha)}
		\path[3d coordinate={(I_1)=(A)+\mya*(\myex)+\myb*(\myey)},
			3d coordinate={(I_2)=(A)+\mya*(\myex)-\myb*(\myey)}];
		\pgfmathsetmacro{\tsta}{sqrt(TD("(B)-(I_1)o(B)-(I_1)"))}	
		\pgfmathsetmacro{\tstb}{sqrt(TD("(B)-(I_2)o(B)-(I_2)"))}	
		\path[overlay] (\myex) coordinate (ex) 	(\myey) coordinate (ey); 	
		\begin{scope}[x={(ex)},y={(ey)}]
		 \draw (A) circle[radius=r1];
		 \draw (B) circle[radius=r2];
		\end{scope}
		\path foreach \X in {A,B,C,I_1,I_2}
		{(\X) node[circle,inner sep=1pt,fill,label=above:{$%
		 \pgfmathparse{TD("(\X)")}%
		 \X=(\pgfmathprintvector\pgfmathresult)$}]{}};
	   \fi
	  \fi
	 \fi 
\end{tikzpicture}
\end{document}
```
![Screen Shot 2020-11-30 at 6.37.15 PM.png](/image?hash=484a08b9fa21c4ccb4d78060a342809745ba37d5a6d69601f77cca4a129e9a0a)

``` \documentclass[border=2mm,tikz]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools,intersections} \begin{document} \tdplotsetmaincoords{60}{150} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={R=5;}] \path (1,2,3) coordinate (I) (-4, 2, 3) coordinate (A) (1, -2, 6) coordinate (B) (1, 5, 7) coordinate (C) (5,2,6) coordinate (D) ; \path pic{3d circle through 3 points={% A={(A)},B={(B)},C={(C)},center name=H}}; \path pic{3d circle through 3 points={% A={(A)},B={(B)},C={(D)},center name= K}}; \tikzset{3d/plane through={(A) and (B) and (C) named pABC}, 3d/plane through={(A) and (B) and (D) named pABD}} \path[3d/project={(H) on pABD}] coordinate (H') [3d/project={(K) on pABC}] coordinate (K'); \tikzset{3d/line through={(H) and (K') named l1}, 3d/line through={(K) and (H') named l2}} \path[3d/intersection of={l1 with l2}] coordinate (P); \path[overlay,3d coordinate={(n)=(H)-(P)x(K)-(P)}]; % normalization of n \pgfmathsetmacro{\myn}{sqrt(TD("(n)o(n)"))} % radius of first circle around H \pgfmathsetmacro{\myrA}{sqrt(TD("(A)-(H)o(A)-(H)"))} % distance H--P \pgfmathsetmacro{\myrB}{sqrt(TD("(P)-(H)o(P)-(H)"))} % distance P to intersections \pgfmathsetmacro{\myrC}{sqrt(\myrA*\myrA-\myrB*\myrB)} % prefactor in linear combinations \pgfmathsetmacro{\myp}{\myrC/\myn} % build intersections \path[overlay,3d coordinate={(I_1)=(P)+\myp*(n)}, 3d coordinate={(I_2)=(P)-\myp*(n)}]; % mark intersections \path[red] foreach \X in {1,2} {(I_\X) node[circle,draw,inner sep=1ex,label=below:{$I_\X$}] {}}; %\path [name intersections={of=c1 and c2}]; \begin{scope}[shift={(I)}] \draw[tdplot_screen_coords] (I) circle[radius=R]; \end{scope} \path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90,H'/90,H'/90,P/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \end{tikzpicture} \end{document} ``` ![Screen Shot 2020-12-01 at 6.31.08 PM.png](/image?hash=d179f6e3e63941ca3b881888ff3d2b3c0e14ca7f75ed86781f6d12a2af7a6382)

Well, I do not know what this screen shot is supposed to tell me, I am not using this program. However, I also think that you should ask a different (and separate) question on this. Generally two circles do not intersect, neither in one or two points. The configuration which you consider is very special. The intersections can be constructed in many ways as the system is overconstrained. This also means that, depending on the strategy employed, one has to make various checks if the circles really intersect. If it is guaranteed that the circles intersect in two points it is very easy to compute their intersection points. (Project the center of the first circle, `A` on the plane in which the other circle sits. This defines a line through the projection, `A'`, and the center of the second circle, `B`. Do the same for `B` and `A` exchanged. The intersection of the two thus defined lines, `I`, is in the middle between the intersections. They are along `(B)-(I)x(A)-(I)`. The distances can be computed from the length of `(I)-(A)` and `rA`, say.) The verification that they do is the more cumbersome part.

You can use the `intersetions` library but this one will also return fake intersections. ``` \documentclass[border=2mm,tikz]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools,intersections} \begin{document} \tdplotsetmaincoords{60}{150} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={R=5;}] \path (1,2,3) coordinate (I) (-4, 2, 3) coordinate (A) (1, -2, 6) coordinate (B) (1, 5, 7) coordinate (C) (5,2,6) coordinate (D) ; \path[every path/.append style={name path global=c1}] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(C)},center name=H}}; \path[every path/.append style={name path global=c2}] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(D)},center name= K}}; %\path [name intersections={of=c1 and c2}]; \begin{scope}[shift={(I)}] \draw[tdplot_screen_coords] (I) circle[radius=R]; \end{scope} \path[name intersections={of=c1 and c2,total=\t}] %\pgfextra{\typeout{\t}} foreach \X in {1,...,\t} {(intersection-\X) node[circle,draw,inner sep=1ex,label=above:$\X$]{}}; \path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1782), ``` \documentclass[border=2mm,tikz]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools,intersections} \begin{document} \tdplotsetmaincoords{60}{150} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={R=5;}] \path (1,2,3) coordinate (I) (-4, 2, 3) coordinate (A) (1, -2, 6) coordinate (B) (1, 5, 7) coordinate (C) (5,2,6) coordinate (D) ; \path[name path= c1] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(C)},center name=H}}; \path[name path= c2] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(D)},center name= K}}; %\path [name intersections={of=c1 and c2}]; \begin{scope}[shift={(I)}] \draw[tdplot_screen_coords] (I) circle[radius=R]; \end{scope} \path foreach \p/\g in {I/0,A/90,B/90,C/90,D/90} { (\p) node[circle,fill,inner sep=1pt,label=\g:{{$\p$}}]{}}; \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1782), Can I make a path of circle pass though three points like this? ``` \path[name path= c1] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(C)},center name=H} name c1}; \path[name path= c2] pic{3d circle through 3 points={% A={(A)},B={(B)},C={(D)},center name=K}}; ``` and find intersections like this ``` \path[3d/aux keys/intersection 1=S, 3d/aux keys/intersection 2=S', 3d/intersection of={c1 with c2}]; ```

@Anonymous, re: [your question](#question), if you want to just mark the intersections, and are able to draw the circles, the 2d intersections will give you the correct result. So is your question to obtain the 3d coordinates?

1 Answer