Is there a sympler way to draw intersection of two spheres? - TeX

TopAnswers TeX

Top Answer

user 3.14159

If I had a feature request for `tikz-3dplot-circleofsphere` then it would be the possibility to switch to Ti*k*Z styles for the circles, i.e. `insert path`, and to name the points at which the hidden curve turns visible or the visible curve turns hidden. However, as this is not possible, at least as of now, I had to hack the styles to be able to access the segments and intersection points. This allows one to draw only the visible parts of the sphere. One actually does not need all the auxiliary coordinates, all that is needed is the centers of the spheres (called `A` and `B` below) and their radii (`RA` and `RB`).

```
\documentclass[tikz,border=2mm, 12 pt]{standalone}
\usepackage{tikz-3dplot-circleofsphere}
\usetikzlibrary{3dtools} 
\usetikzlibrary{decorations.pathreplacing}
\tikzset{record final point on curve as/.style={postaction={decoration={show path construction,
      curveto code={
	   \path (\tikzinputsegmentlast) coordinate (#1);
      }},decorate}}}
\makeatletter
\tikzset{reuse path/.code={\pgfsyssoftpath@setcurrentpath{#1}}}
\makeatother
\begin{document}
\tdplotsetmaincoords{70}{100}
\begin{tikzpicture}[scale=1,tdplot_main_coords,
	declare function={RA=6;RB=8;}]
  \path  (3,2,8) coordinate (A) % radius R1
      (3,-4,0) coordinate (B); % radius R
  \path[overlay] [3d coordinate={(myn)=(B)-(A)}];
  \pgfmathsetmacro{\myd}{sqrt(TD("(myn)o(myn)"))}
  \pgfmathsetmacro{\mygammaA}{acos((RB*RB+\myd*\myd-RA*RA)/(2*RB*\myd))}
  \pgfmathsetmacro{\mygammaB}{-acos((RA*RA+\myd*\myd-RB*RB)/(2*RA*\myd))}
  \pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")}
  \pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]}
  \pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]}
  \pgfmathsetmacro{\myn}{TD("(myn)")}
  \pgfmathtruncatemacro{\ltest}{(screendepth(\myn)>0?1:-1)}
  \ifnum\ltest<0
	\begin{scope}[shift={(B)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RB}{\myalpha}{\mybeta}{\mygammaB}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$),
 		\n1={atan2(\y1,\x1)},\n2={360+atan2(\y2,\x2)} 
	  in [reuse path=\pathB] (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB];
	 \fill[ball color=red,opacity=0.6] (B) circle[radius=RB];
	 \end{scope}
	\end{scope}
	\begin{scope}[shift={(A)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RA}{\myalpha}{\mybeta}{\mygammaA}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$),
 		\n1={360+atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} 
	  in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA];
	 \fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA];
	 \end{scope}
	\end{scope}
  \else
	\begin{scope}[shift={(A)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RA}{\myalpha}{\mybeta}{\mygammaA}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$),
 		\n1={360+atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} 
	  in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA];
	 \fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA];
	 \end{scope}
	\end{scope}
	\begin{scope}[shift={(B)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RB}{\myalpha}{\mybeta}{\mygammaB}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$),
 		\n1={atan2(\y1,\x1)},\n2={360+atan2(\y2,\x2)} 
	  in [reuse path=\pathB] (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB];
	 \fill[ball color=red,opacity=0.6] (B) circle[radius=RB];
	 \end{scope}
	\end{scope}
  \fi
  \foreach \p/\g in {A/90,B/-90}
  {\draw[fill=black] (\p) circle[radius=1.5pt];
   \path (\p)+(\g:3mm) node{$\p$};}
\end{tikzpicture}
\end{document}
```

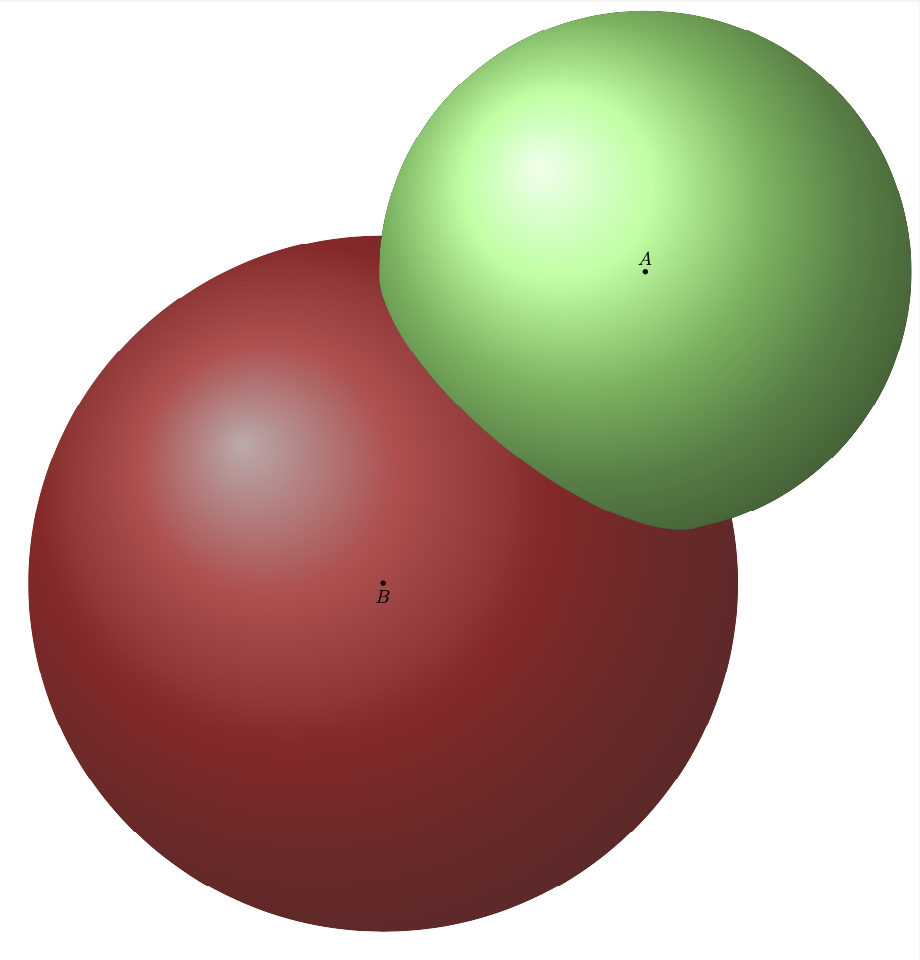
![Screen Shot 2020-11-25 at 6.44.00 AM.png](/image?hash=e19059e23d74d2f5cfce9131c6bc3e8ded063d375f0bfbd27629a022b3eb64f7)

To create the nowadays mandatory animation one has to hack even more because we do not have to clip if the intersection path is completely visible.
```
\documentclass[tikz,border=2mm, 12 pt]{standalone}
\usepackage{tikz-3dplot-circleofsphere}
\usetikzlibrary{3dtools} 
\usetikzlibrary{decorations.pathreplacing}
\tikzset{record final point on curve as/.style={postaction={decoration={show path construction,
      curveto code={
	   \path (\tikzinputsegmentlast) coordinate (#1);
      }},decorate}},
	  memorize hidden stretch/.code={\global\tikztdhashiddenstretchtrue},
	  declare function={maxangle(\a,\b)=ifthenelse(abs(\b-\a)<180,\b+360,\b);}}
\makeatletter
\tikzset{reuse path/.code={\pgfsyssoftpath@setcurrentpath{#1}}}
\makeatother
\newif\iftikztdhashiddenstretch
\tikztdhashiddenstretchfalse
\begin{document}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{70}{\Angle}
\begin{tikzpicture}[scale=1,tdplot_main_coords,
	declare function={RA=6;RB=8;}]
  \path[use as bounding box,tdplot_screen_coords] 
  	(-402pt,-305pt) rectangle (402pt,426pt);	
  \path  (3,2,8) coordinate (A) % radius R1
      (3,-4,0) coordinate (B); % radius R
  \path[overlay] [3d coordinate={(myn)=(B)-(A)}];
  \pgfmathsetmacro{\myd}{sqrt(TD("(myn)o(myn)"))}
  \pgfmathsetmacro{\mygammaA}{acos((RB*RB+\myd*\myd-RA*RA)/(2*RB*\myd))}
  \pgfmathsetmacro{\mygammaB}{-acos((RA*RA+\myd*\myd-RB*RB)/(2*RA*\myd))}
  \pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")}
  \pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]}
  \pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]}
  \pgfmathsetmacro{\myn}{TD("(myn)")}
  \pgfmathtruncatemacro{\ltest}{(screendepth(\myn)>0?1:-1)}
  \ifnum\ltest<0
	\begin{scope}[shift={(B)}]
	 \tikztdhashiddenstretchfalse
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux',
		memorize hidden stretch}]{RB}{\myalpha}{\mybeta}{\mygammaB}  
	 \begin{scope}[tdplot_screen_coords]
	 \iftikztdhashiddenstretch
	  \clip let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$),
 		 \n1={atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in
		[reuse path=\pathB] -- (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB];
	  \fi	   
	 \fill[ball color=red,opacity=0.6] (B) circle[radius=RB];
	 \end{scope}
	\end{scope}
	\begin{scope}[shift={(A)}]
	 \tikztdhashiddenstretchfalse
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux',
		memorize hidden stretch}]{RA}{\myalpha}{\mybeta}{\mygammaA}  
	 \begin{scope}[tdplot_screen_coords]
	  \iftikztdhashiddenstretch
	   \clip let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$),
 		  \n1={360+atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} 
		in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA];
	   \fi 
	  \fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA];
	 \end{scope}
	\end{scope}
  \else
	\begin{scope}[shift={(A)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RA}{\myalpha}{\mybeta}{\mygammaA}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$),
 		\n1={360+atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} 
	  in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA];
	 \fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA];
	 \end{scope}
	\end{scope}
	\begin{scope}[shift={(B)}]
	 \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux},
 		tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RB}{\myalpha}{\mybeta}{\mygammaB}  
	 \begin{scope}[tdplot_screen_coords]
	 \clip let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$),
 		\n1={atan2(\y1,\x1)},\n2={360+atan2(\y2,\x2)} 
	  in [reuse path=\pathB] (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB];
	 \fill[ball color=red,opacity=0.6] (B) circle[radius=RB];
	 \end{scope}
	\end{scope}
  \fi
  \foreach \p/\g in {A/90,B/-90}
  {\draw[fill=black] (\p) circle[radius=1.5pt];
   \path (\p)+(\g:3mm) node{$\p$};}
\end{tikzpicture}}
\end{document}
```
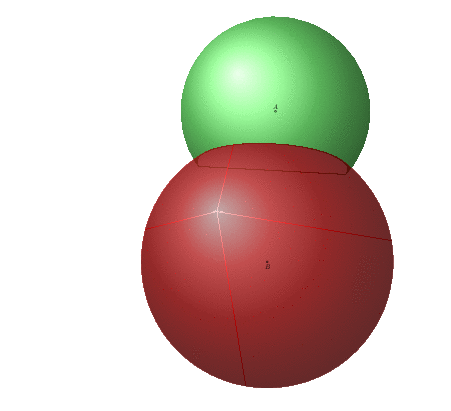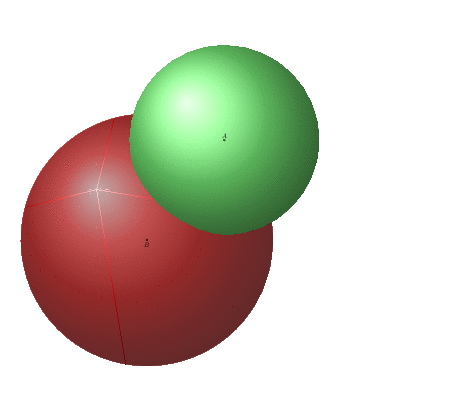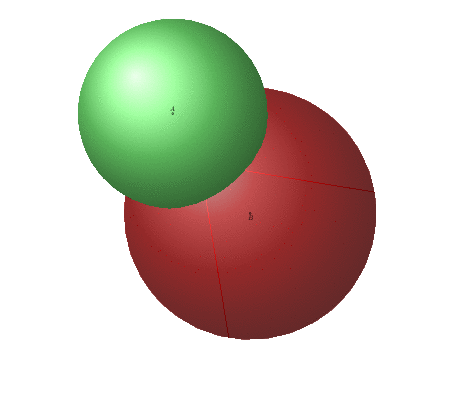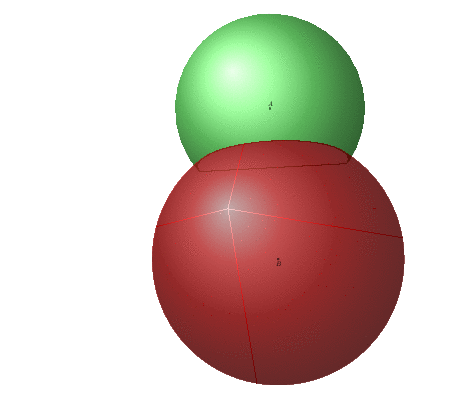
![ani.gif](/image?hash=e9a27e77f070ea61ac399e1921a5d2a475cf7b8942ff09e82dd9366bc68677c2)
The spurious lines are due to the conversion from pdf to gif, they are absent on the pdf.

You can ask them any LaTeX question. They know everything better, at least that's what they say. And they have a "mathematician working in algebra" among their friends. They refer to their own codes as "clean", of course implying that the codes by others are not so clean, accuse others falsely of spying on them, not reading or misrepresenting the facts. This allows one to get a pretty good idea of how they operate. I will take a rest and just wait and see if there is a site in which users exchange LaTeX codes rather than worshipping some aggressive actors whose main interest is to show off and to step on others.

As you can see, I am no longer active. I am sorry if this is inconvenient. This site has also been taken over by the expl3 activists, who insult anyone who does not agree with them, promote falsehoods, and upvote each others posts regardless of the contents. Since I do not enjoy getting insults I am out of here. I hope you can find others with whom you can chat...

@marmot, re: [your answer](#a1773), My code ``` \documentclass[border=2mm]{standalone} \usepackage{tikz} \usetikzlibrary{decorations.pathreplacing,3dtools,angles,calc}% https://github.com/marmotghost/tikz-3dtools \begin{document} \begin{tikzpicture}[3d/install view={phi=70,theta=70},line cap=butt,line join=round,c/.style={circle,fill,inner sep=1pt},declare function={r=2;R=2*r;d=r+R;}] \path (0,0,0) coordinate (A) (0,2*r,0) coordinate (B) ({r*sqrt(3)},r,0) coordinate (C); \pgfmathsetmacro{\mybarycenter}{barycenter("(A),(B),(C)")} \path (\mybarycenter) coordinate (G); \path [save named path=sphA,3d/screen coords] (A) circle[radius=r]; \path [save named path=sphC,3d/screen coords] (C) circle[radius=r]; \path [save named path=sphB,3d/screen coords] (B) circle[radius=r]; \path[overlay,3d/intersection of three spheres= {rA=d,rB=d,rC=d}]; \path[overlay] (i2) coordinate (S); \path [save named path=sphS,3d/screen coords] (S) circle[radius=R]; \path[save named path=pyra,convex hull of={A,B,C,S}]; \tikzset{3d/ordered paths/.cd,sphA/.style={red},sphB/.style={blue},sphC/.style={cyan},sphS/.style={purple},pyra/.style={draw = none}} \tikzset{3d/draw ordered paths={sphA,sphB,sphC,sphS,pyra}} \path foreach \p/\g in {A/180,B/-90,C/-90,G/0,S/0} {(\p)node[c]{}+(\g:2.5mm) node{$\p$}}; \draw[3d/hidden] (A) -- (B) -- (C) -- cycle (G) -- (A) (G) -- (B) (G) -- (C) (S) -- (A) (S) -- (B) (S) -- (C) (S) -- (G) ; \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1773), Please comment for me about this code when I draw this problem Three mutually tangent spheres of radius $1$ rest on a horizontal plane. A sphere of radius $2$ rests on them. What is the distance from the plane to the top of the larger sphere?

Here is something of that sort. ``` \documentclass[tikz,border=2mm, 12 pt]{standalone} \usepackage{tikz-3dplot-circleofsphere} \usetikzlibrary{3dtools} \usetikzlibrary{decorations.pathreplacing} \tikzset{record final point on curve as/.style={postaction={decoration={show path construction, curveto code={ \path (\tikzinputsegmentlast) coordinate (#1); },lineto code={ \path (\tikzinputsegmentlast) coordinate (#1); }},decorate}}, memorize hidden stretch/.code={\global\tikztdhashiddenstretchtrue}, memorize visible stretch/.code={\global\tikztdhasvisiblestretchtrue}, declare function={maxangle(\a,\b)=ifthenelse(abs(\b-\a)<180, ifthenelse(\b<\a,\b+360,\b-360),\b); minangle(\a,\b)=ifthenelse(abs(\b-\a)<180,\b, ifthenelse(\b<\a,\b+360,\b-360)); }} \makeatletter \tikzset{reuse path/.code={\pgfsyssoftpath@setcurrentpath{#1}}} \makeatother \newif\iftikztdhashiddenstretch \tikztdhashiddenstretchfalse \newif\iftikztdhasvisiblestretch \tikztdhasvisiblestretchfalse \newcommand{\DrawTwoCircles}[3][]{% mygamma \begin{scope}[shift={(#2)}] \tikztdhashiddenstretchfalse \tikztdhasvisiblestretchfalse \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\tmppath, record final point on curve as=aux,memorize visible stretch}, tdplotCsBack/.style={draw=none,record final point on curve as=aux', memorize hidden stretch}]{R#2}{\myalpha}{\mybeta}{\mygamma} \iftikztdhasvisiblestretch \else \tikztdhashiddenstretchfalse \fi \begin{scope}[tdplot_screen_coords] % hidden lines \iftikztdhashiddenstretch %\typeout{has hidden and visiblestretch} \clip let \p1=($(aux)-(#2)$),\p2=($(aux')-(#2)$), \n1={atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in [reuse path=\tmppath] -- (\n1:R#2) arc[start angle=\n1,end angle=\n2,radius=R#2]; \else \clip (#2) circle[radius=R#2]; \fi \draw[c#3,hidden] (#3) circle[radius=R#3]; \end{scope} % visible \begin{scope}[tdplot_screen_coords] \iftikztdhashiddenstretch \clip[even odd clip] let \p1=($(aux)-(#2)$),\p2=($(aux')-(#2)$), \n1={atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in [reuse path=\tmppath] -- (\n1:R#2) arc[start angle=\n1,end angle=\n2,radius=R#2] [generous outside path']; \else \clip[even odd clip] (#2) circle[radius=R#2] [generous outside path']; \fi \draw[c#3,visible] (#3) circle[radius=R#3]; \end{scope} % circle #2 in the front \begin{scope}[tdplot_screen_coords] \iftikztdhashiddenstretch \draw[hidden,c#2] let \p1=($(aux)-(#2)$),\p2=($(aux')-(#2)$), \n1={atan2(\y1,\x1)},\n2={minangle(\n1,atan2(\y2,\x2))} in (\n1:R#2) arc[start angle=\n1,end angle=\n2,radius=R#2]; \draw[visible,c#2] let \p1=($(aux)-(#2)$),\p2=($(aux')-(#2)$), \n1={atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in [reuse path=\tmppath] -- (\n1:R#2) arc[start angle=\n1,end angle=\n2,radius=R#2]; \else \draw[visible,c#2] (#2) circle[radius=R#2]; \fi \end{scope} \end{scope} } \begin{document} \foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{70}{\Angle} \begin{tikzpicture}[scale=1,tdplot_main_coords, declare function={RA=6;RB=8;}, cA/.style={red},cB/.style={blue}, visible/.style={draw,solid}, hidden/.style={draw,very thin,cheating dash}] \path[use as bounding box,tdplot_screen_coords] (-402pt,-305pt) rectangle (402pt,426pt); \path (3,2,8) coordinate (A) % radius R1 (3,-4,0) coordinate (B); % radius R \path[overlay] [3d coordinate={(myn)=(B)-(A)}, 3d coordinate={(nscreen)=(nscreenx,nscreeny,nscreenz)}, 3d coordinate={(ntest)=(myn)x(nscreen)}]; \pgfmathsetmacro{\myn}{TD("(myn)"))} \pgfmathsetmacro{\dtest}{sqrt(TD("(ntest)o(ntest)"))} \pgfmathtruncatemacro{\ltest}{(screendepth(\myn)>0?1:-1)} \ifdim\dtest pt<0.2pt % in this case the circles are on top of each other % so we need only to draw two circles \ifnum\ltest<0 \draw[tdplot_screen_coords,cB] (B) circle[radius=RB]; \draw[tdplot_screen_coords,cA] (A) circle[radius=RA]; \else \draw[tdplot_screen_coords,cA] (A) circle[radius=RA]; \draw[tdplot_screen_coords,cB] (B) circle[radius=RB]; \fi \else \pgfmathsetmacro{\myd}{sqrt(TD("(myn)o(myn)"))} \pgfmathsetmacro{\mygammaA}{acos((RB*RB+\myd*\myd-RA*RA)/(2*RB*\myd))} \pgfmathsetmacro{\mygammaB}{-acos((RA*RA+\myd*\myd-RB*RB)/(2*RA*\myd))} \pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")} \pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]} \pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]} \pgfmathsetmacro{\myn}{TD("(myn)")} \ifnum\ltest<0 % A in front of B \let\mygamma\mygammaA \DrawTwoCircles{A}{B} \else % B in front of A \let\mygamma\mygammaB \DrawTwoCircles{B}{A} \fi \foreach \p/\g/\t in {A/90/{A},B/-90/B} {\draw[fill=black] (\p) circle[radius=1.5pt]; \path (\p)+(\g:3mm) node{$\t$};} \fi \end{tikzpicture}} \end{document}

How about dashed line of circle and sphere? Can I get like this? ![ScreenHunter 960.png](/image?hash=5f76f585823edeb42448a7e0a12932be3574a35934b6b09e4032982c9a6188a8) ![ScreenHunter 961.png](/image?hash=ffd0c7893e50c53b80d64054130d7894b32719698623a196fe5d285af62e2cdb)

Here is the code you seem to be asking for. ``` \documentclass[tikz,border=2mm, 12 pt]{standalone} \usepackage{tikz-3dplot-circleofsphere} \usetikzlibrary{3dtools} \usetikzlibrary{decorations.pathreplacing} \tikzset{record final point on curve as/.style={postaction={decoration={show path construction, curveto code={ \path (\tikzinputsegmentlast) coordinate (#1); }},decorate}}, memorize hidden stretch/.code={\global\tikztdhashiddenstretchtrue}, declare function={maxangle(\a,\b)=ifthenelse(abs(\b-\a)<180,\b+360,\b);}} \makeatletter \tikzset{reuse path/.code={\pgfsyssoftpath@setcurrentpath{#1}}} \makeatother \newif\iftikztdhashiddenstretch \tikztdhashiddenstretchfalse \begin{document} \foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{70}{\Angle} \begin{tikzpicture}[scale=1,tdplot_main_coords, declare function={RA=6;RB=8;}] \path[use as bounding box,tdplot_screen_coords] (-402pt,-305pt) rectangle (402pt,426pt); \path (3,2,8) coordinate (A) % radius R1 (3,-4,0) coordinate (B); % radius R \path[overlay] [3d coordinate={(myn)=(B)-(A)}]; \pgfmathsetmacro{\myd}{sqrt(TD("(myn)o(myn)"))} \pgfmathsetmacro{\mygammaA}{acos((RB*RB+\myd*\myd-RA*RA)/(2*RB*\myd))} \pgfmathsetmacro{\mygammaB}{-acos((RA*RA+\myd*\myd-RB*RB)/(2*RA*\myd))} \pgfmathsetmacro{\myaxisangles}{axisangles("(myn)")} \pgfmathsetmacro{\myalpha}{{\myaxisangles}[0]} \pgfmathsetmacro{\mybeta}{{\myaxisangles}[1]} \pgfmathsetmacro{\myn}{TD("(myn)")} \pgfmathtruncatemacro{\ltest}{(screendepth(\myn)>0?1:-1)} \ifnum\ltest<0 \begin{scope}[shift={(B)}] \tikztdhashiddenstretchfalse \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux}, tdplotCsBack/.style={draw=none,record final point on curve as=aux', memorize hidden stretch}]{RB}{\myalpha}{\mybeta}{\mygammaB} \begin{scope}[tdplot_screen_coords,draw=red] \iftikztdhashiddenstretch \draw[clip] let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$), \n1={atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in [reuse path=\pathB] -- (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB]; \fi %\fill[ball color=red,opacity=0.6] (B) circle[radius=RB]; \draw[red] (B) circle[radius=RB]; \end{scope} \end{scope} \begin{scope}[shift={(A)}] \tikztdhashiddenstretchfalse \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux}, tdplotCsBack/.style={draw=none,record final point on curve as=aux', memorize hidden stretch}]{RA}{\myalpha}{\mybeta}{\mygammaA} \begin{scope}[tdplot_screen_coords,draw=blue] \iftikztdhashiddenstretch \draw[clip] let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$), \n1={360+atan2(\y1,\x1)},\n2={maxangle(\n1,atan2(\y2,\x2))} in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA]; \fi %\fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA]; \draw (A) circle[radius=RA]; \end{scope} \end{scope} \else \begin{scope}[shift={(A)}] \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathA,record final point on curve as=aux}, tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RA}{\myalpha}{\mybeta}{\mygammaA} \begin{scope}[tdplot_screen_coords,draw=blue] \draw[clip] let \p1=($(aux)-(A)$),\p2=($(aux')-(A)$), \n1={360+atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} in [reuse path=\pathA] (\n1:RA) arc[start angle=\n1,end angle=\n2,radius=RA]; %\fill[ball color=green!50, opacity=1.0] (A) circle[radius=RA]; \draw (A) circle[radius=RA]; \end{scope} \end{scope} \begin{scope}[shift={(B)}] \tdplotCsDrawCircle[tdplotCsFront/.style={draw=none,save path=\pathB,record final point on curve as=aux}, tdplotCsBack/.style={draw=none,record final point on curve as=aux'}]{RB}{\myalpha}{\mybeta}{\mygammaB} \begin{scope}[tdplot_screen_coords,draw=red] \draw[clip] let \p1=($(aux)-(B)$),\p2=($(aux')-(B)$), \n1={atan2(\y1,\x1)},\n2={360+atan2(\y2,\x2)} in [reuse path=\pathB] (\n1:RB) arc[start angle=\n1,end angle=\n2,radius=RB]; %\fill[ball color=red,opacity=0.6] \draw (B) circle[radius=RB]; \end{scope} \end{scope} \fi \foreach \p/\g in {A/90,B/-90} {\draw[fill=black] (\p) circle[radius=1.5pt]; \path (\p)+(\g:3mm) node{$\p$};} \end{tikzpicture}} \end{document} ```

Why? It is not supposed to yield the correct contour for the sphere that is further away but only cut the closer one appropriately, if that's what you mean. (One could cut the further away one, too, but this would be quite some effort.)

1 Answer