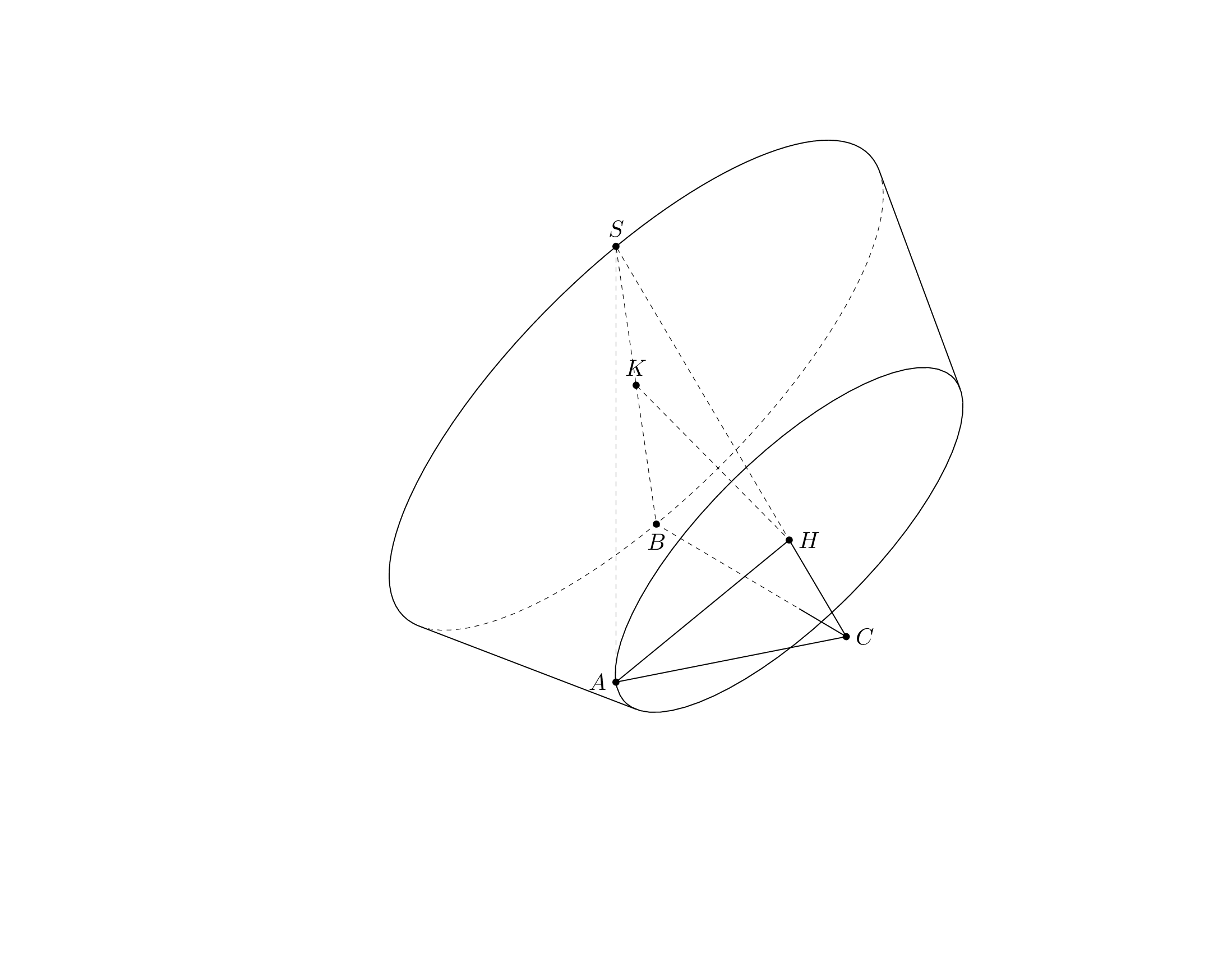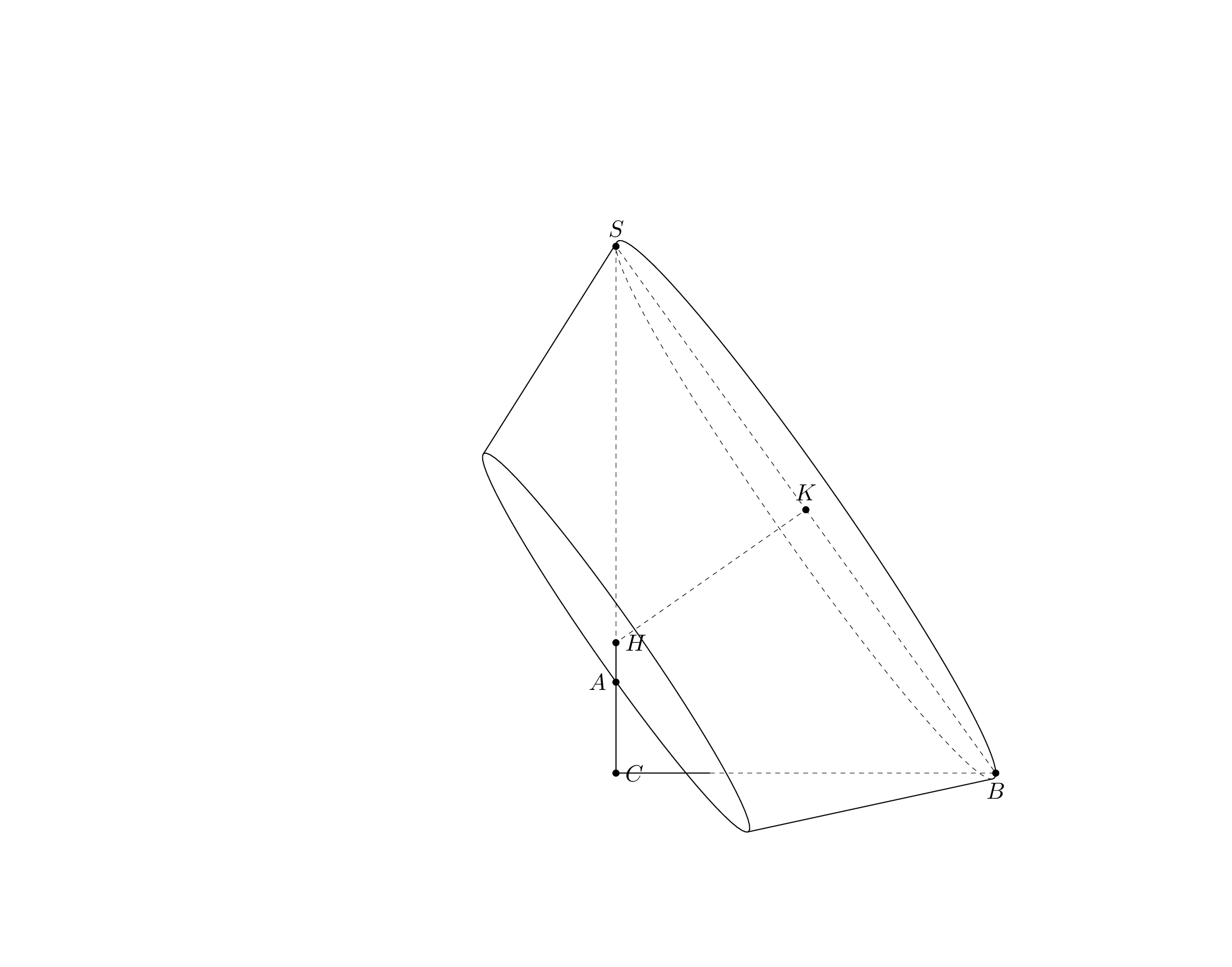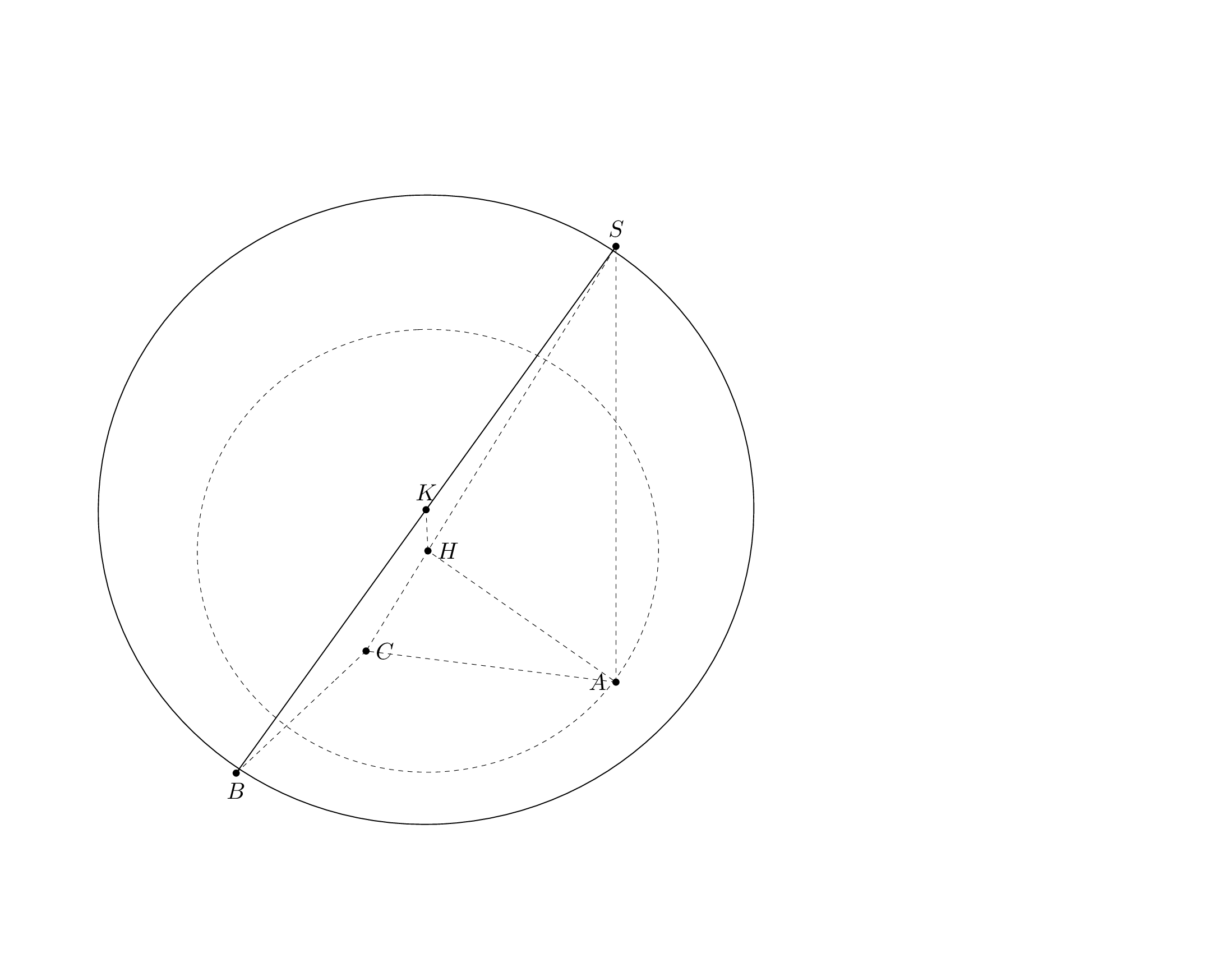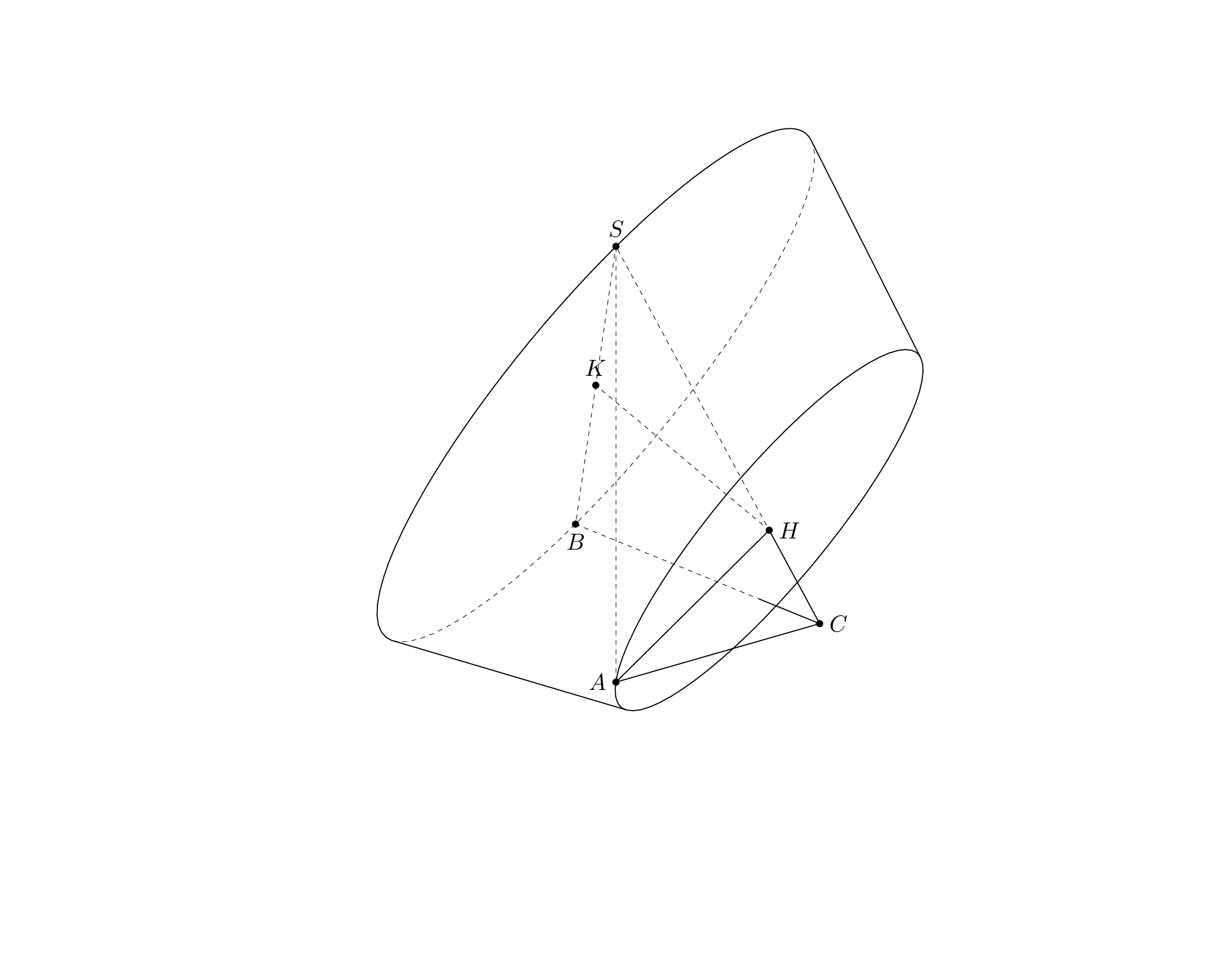
This is what I was able to do within the time I have now. First of all, here is a `pic` for the frustum, which does the dashed lines for this one correctly, hopefully. (If not, this is a solvable problem, I think.) 

```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot} 
\usetikzlibrary{3dtools}
\usepackage{tikz-3dplot-circleofsphere}
% https://tex.stackexchange.com/a/59168
\tikzset{reverseclip/.style={overlay,insert path={[reset cm]
			(-16383.99999pt,-16383.99999pt) |-
			(16383.99999pt,16383.99999pt)|- cycle}},
		 reverseclip'/.style={overlay,insert path={[reset cm]
			(-16383.99999pt,-16383.99999pt) -|
			(16383.99999pt,16383.99999pt)-| cycle}}}
\tikzset{pics/3d/frustum/.style={code={
			\tikzset{3d/frustum/.cd,#1}
			\def\pv##1{\pgfkeysvalueof{/tikz/3d/frustum/##1}}%
			\pgfmathsetmacro{\myH}{(\pv{R}*\pv{h}/(\pv{R}-\pv{r}))}%
			\pgfmathsetmacro{\sdtip}{screendepth(0,0,\myH)}%
			\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\myH*\myH-\sdtip*\sdtip))}
			%\typeout{H=\myH,angle=\aspectangle}
			\path[overlay] (0,0,\myH) coordinate (-tip)
			(0,0,\pv{h}) coordinate (-upper base);
			\begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}]
				\pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{R}/\myH)<1}
				\ifnum\itest=1
				 \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{R}/\myH)}
				 \ifdim\sdtip pt>0pt
				  \path[/tikz/3d/frustum/hidden] (\alphacrit:\pv{R}) arc[start angle=\alphacrit,end
				  angle=-\alphacrit,radius=\pv{R}];
				  \path[/tikz/3d/frustum/visible] ($(-upper base)+(\alphacrit:\pv{r})$)
				  --(\alphacrit:\pv{R}) 
				  arc[start angle=\alphacrit,end  angle=360-\alphacrit,radius=\pv{R}]
				  -- ($(-upper base)+(360-\alphacrit:\pv{r})$);
				  \path[/tikz/3d/frustum/visible] (-upper base) circle[radius=\pv{r}];
				 \else %\typeout{\sdtip<0}
				  \path[/tikz/3d/frustum/visible] circle[radius=\pv{R}];
				  \begin{scope}
				   \clip circle[radius=\pv{R}];
				   \path[/tikz/3d/frustum/hidden] ($(-upper base)+(\alphacrit:\pv{r})$)
				   --(\alphacrit:\pv{R}) 
				   ($(-upper base)+(360-\alphacrit:\pv{r})$)
				   --(360-\alphacrit:\pv{R});
				   \path[/tikz/3d/frustum/hidden] (-upper base) circle[radius=\pv{r}];
				  \end{scope}
				  % enlarge the bounding box
				  \path ($(-upper base)+(\alphacrit:\pv{r})$)
				  --(\alphacrit:\pv{R}) 
				  ($(-upper base)+(360-\alphacrit:\pv{r})$)
				  --(360-\alphacrit:\pv{R});
				  \path (-upper base) circle[radius=\pv{r}];
				  \begin{scope}
 				   \clip circle[radius=\pv{R}] [reverseclip'];
				   \path[/tikz/3d/frustum/visible] ($(-upper base)+(\alphacrit:\pv{r})$)
				   --(\alphacrit:\pv{R}) 
				   ($(-upper base)+(360-\alphacrit:\pv{r})$)
				   --(360-\alphacrit:\pv{R});
				   \path[/tikz/3d/frustum/visible] (-upper base) circle[radius=\pv{r}];
				  \end{scope}
				 \fi
				\else
				 \path[/tikz/3d/frustum/visible] circle[radius=\pv{R}];	 
				\fi
			\end{scope}
	}},
	3d/frustum/.cd,R/.initial=2,r/.initial=1,h/.initial=1,
	visible/.style={draw,solid},
	hidden/.style={draw,very thin,cheating dash}}
\begin{document} 
\foreach \Angle in {5,15,...,355}
	{\tdplotsetmaincoords{70}{\Angle}
	\begin{tikzpicture}[tdplot_main_coords,scale=1,line cap=butt,
		line join=round,declare function={a=7;R=a/2; angC =-20;h=a;},
		tdplotCsBack/.style={cheating dash},
		visible/.style={draw,solid},
		hidden/.style={draw,very thin,cheating dash}]
		\path[use as bounding box,tdplot_screen_coords]
		 (-9,-4) rectangle (9,10);
		\path
		(0,0,0) coordinate (A)
		(0,a,0)  coordinate (B)
		({ R*cos(angC)}, {a/2 + R*sin(angC)},0) coordinate (C)
		(0,0,h) coordinate (S)
		%[3d coordinate={(O)=0.5*(A)+0.5*(C)}];
		; 
		\path[3d/line through={(S) and (B) named lSB}];
		\path[3d/line through={(S) and (C) named lSC}];
		\path[3d/project={(A) on lSC}] coordinate (H);
		\path[3d/project={(H) on lSB}] coordinate (K);	
		\path[overlay,3d coordinate={(K')=(H)-(K)x(S)-(K)},
		3d coordinate={(K'')=(K)+(K')},
		3d coordinate={(N)=(H)-(K)}];
		\path[3d/define orthonormal dreibein={A={(K)},B={(S)},C={(K'')}}];
		\pgfmathsetmacro{\R}{sqrt(TD("(K)-(S)o(K)-(S)")}
		\pgfmathsetmacro{\r}{sqrt(TD("(A)-(H)o(A)-(H)")}
		\pgfmathsetmacro{\h}{sqrt(TD("(K)-(H)o(K)-(H)")}
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
			\path (K) pic{3d/frustum={R=\R,r=\r,h=\h}};
			\fill (-upper base) circle[radius=1pt];
		\end{scope}
		\tikzset{3d/.cd,
		plane with normal={(N) through (H) named pU},
		line through={(B) and (C) named lBC}}
		\path[3d/intersection of={lBC with pU}] coordinate (B');
		%
		\pgfmathsetmacro{\myN}{TD("(N)")}
		\pgfmathsetmacro{\ltest}{screendepth(\myN)}
		\ifdim\ltest pt<0pt
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
		  \clip (H) circle[radius=\r];
		  \draw[hidden] (A) -- (C) -- (H) -- cycle (C)--(B')  ;
		\end{scope}
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
		  \clip (H) circle[radius=\r] [reverseclip'];
		  \draw[visible] (A) -- (C) -- (H) -- cycle (C)--(B')  ;
		\end{scope}
		 \draw[hidden]  (B) -- (B') 
		  (A) -- (S) -- (H) -- (K) -- (S) ;   	
		 \draw[visible] (S) -- (K) -- (B);
		\else
		 \draw[visible] (A) -- (C) -- (H) -- cycle
		  (C)--(B')  ;
		 \draw[hidden]  (K) --  (B) -- (B') 
		  (A) -- (S) -- (H) -- (K) -- (S) ;   	
		\fi 
		\foreach \v/\position in 
		{B/below,C/right,A/left,S/above,K/above,H/right} {\draw[draw =black, fill=black] (\v) circle (1.3pt) node [\position=0.2mm] {$\v$}; 
		} 		
	\end{tikzpicture}} 
\end{document}
```
![ani.gif](/image?hash=a797aeb4c8193c91d7eb18f994bd01dc553a8826085f94b32e13946f59eeeeba)

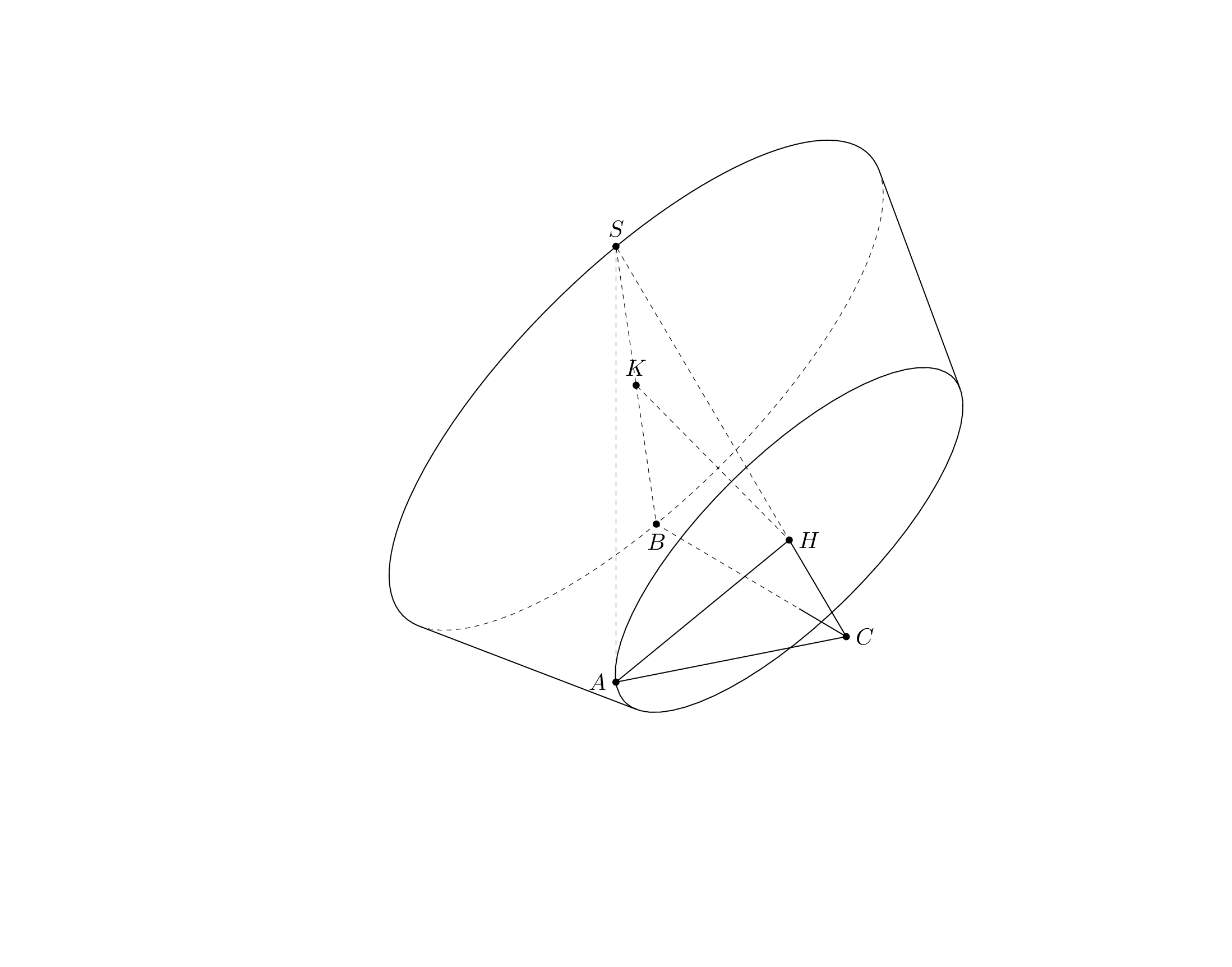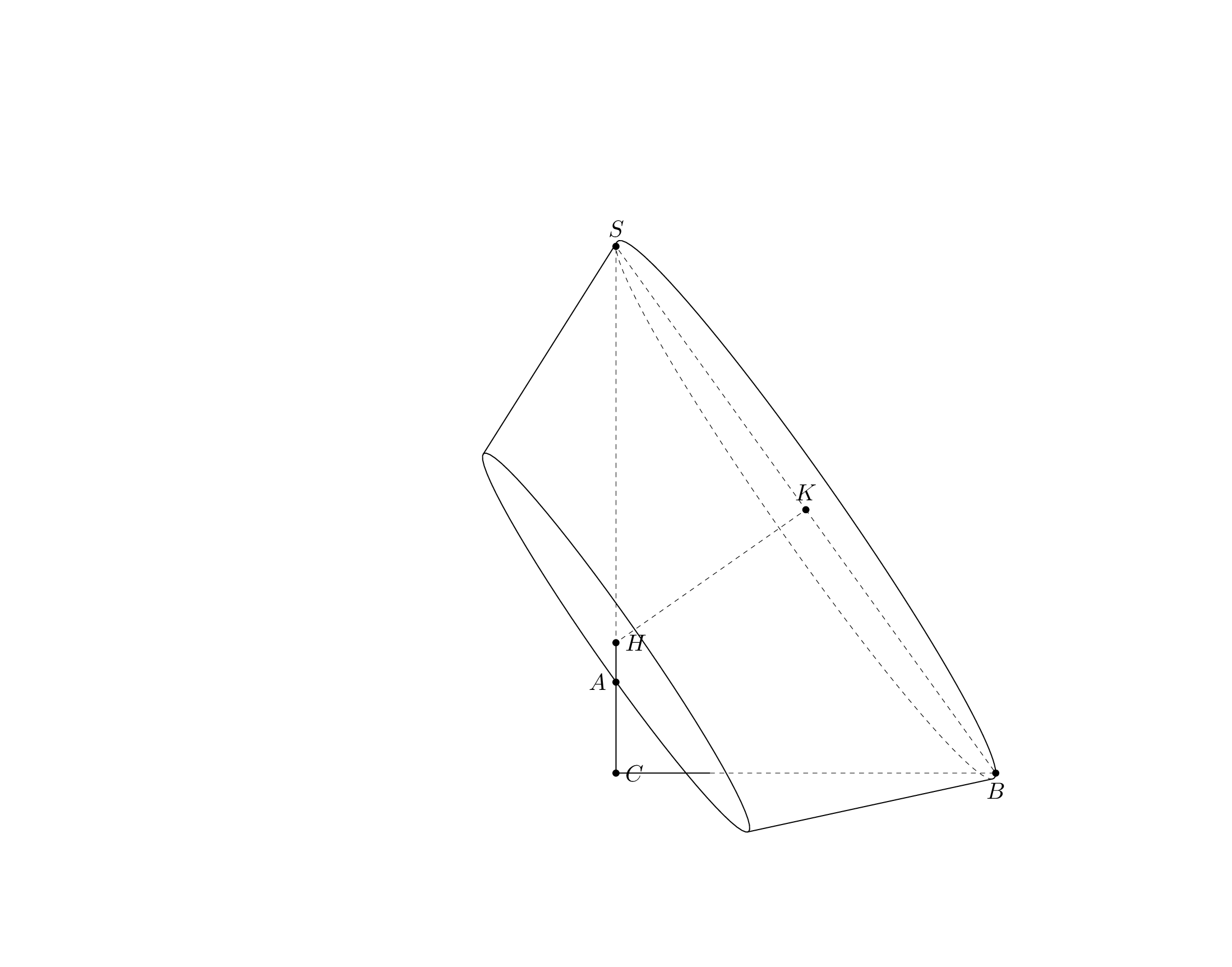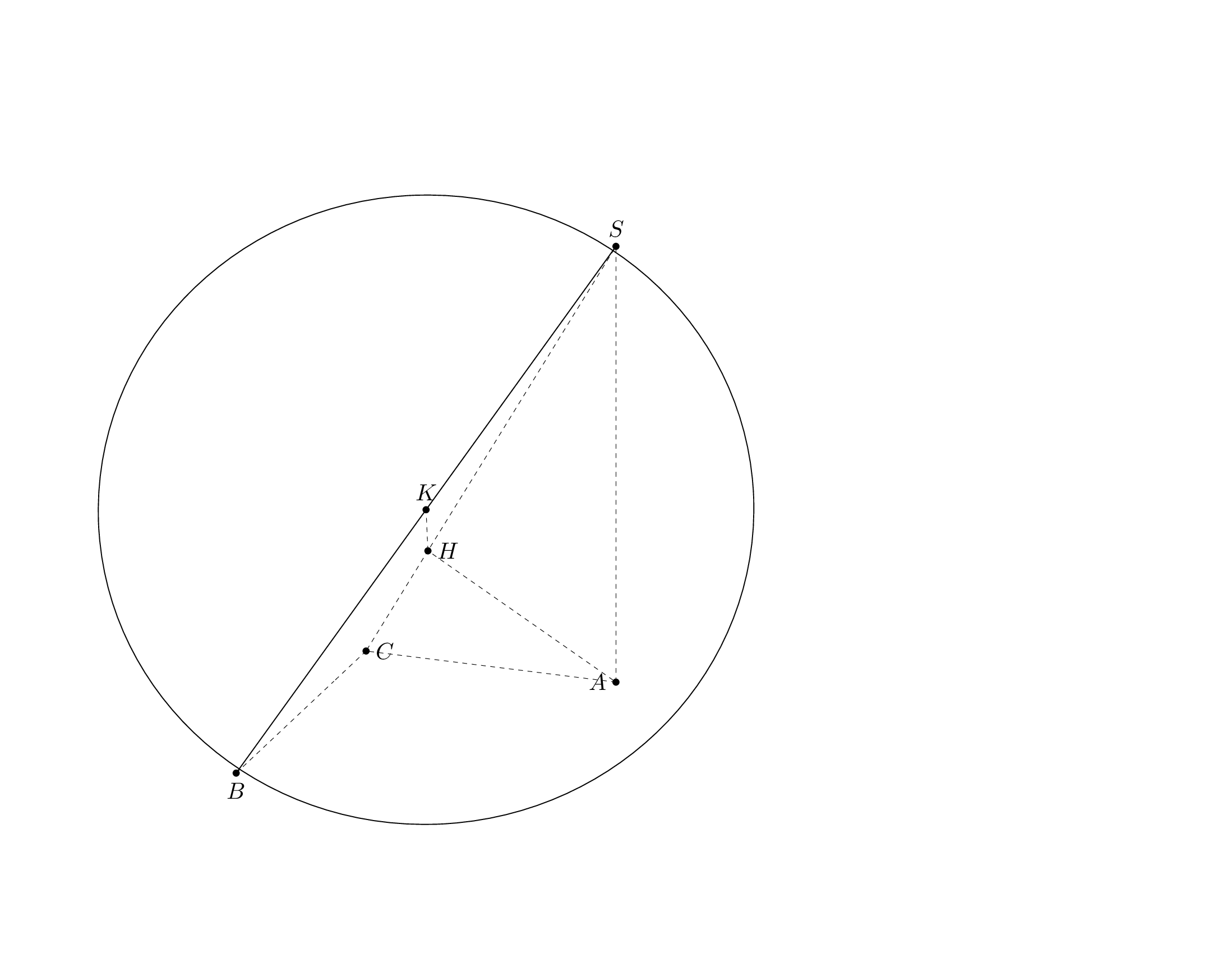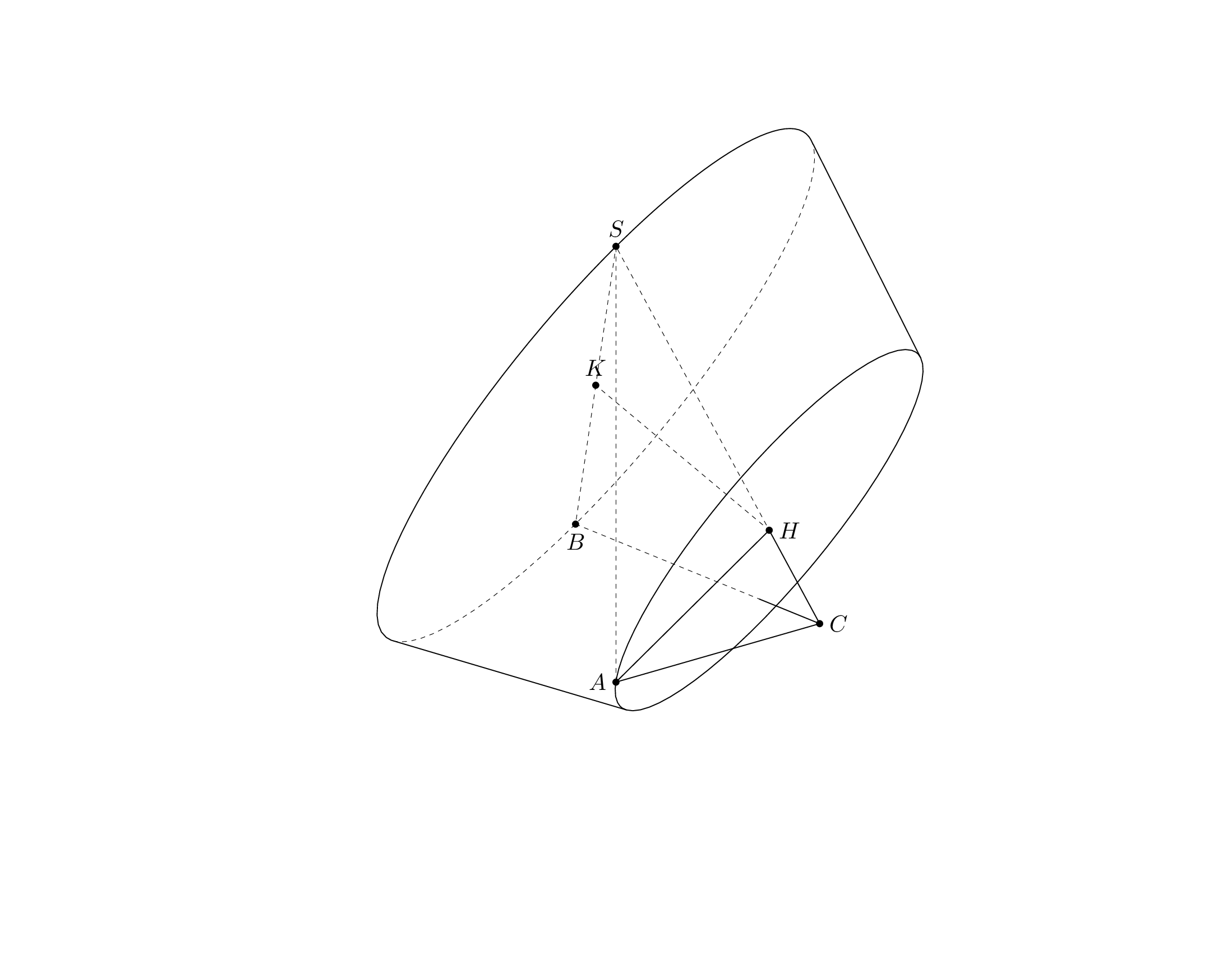
Per request I added the `frustum` to the [`3dtools` library](https://github.com/marmotghost/tikz-3dtools). It is slightly different since it shares some keys with other 3d pics, see [the manual](https://github.com/marmotghost/tikz-3dtools/blob/master/3DToolsManual.pdf). Once I have more time I will add a better cylinder.
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot} 
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\usepackage{tikz-3dplot-circleofsphere}
\begin{document} 
\foreach \Angle in {5,15,...,355}
	{\tdplotsetmaincoords{70}{\Angle}
	\begin{tikzpicture}[tdplot_main_coords,scale=1,line cap=butt,
		line join=round,declare function={a=7;R=a/2; angC =-20;h=a;},
		tdplotCsBack/.style={cheating dash},
		visible/.style={draw,solid},
		hidden/.style={draw,very thin,cheating dash}]
		\path[use as bounding box,tdplot_screen_coords]
		 (-9,-4) rectangle (9,10);
		\path
		(0,0,0) coordinate (A)
		(0,a,0)  coordinate (B)
		({ R*cos(angC)}, {a/2 + R*sin(angC)},0) coordinate (C)
		(0,0,h) coordinate (S)
		%[3d coordinate={(O)=0.5*(A)+0.5*(C)}];
		; 
		\path[3d/line through={(S) and (B) named lSB}];
		\path[3d/line through={(S) and (C) named lSC}];
		\path[3d/project={(A) on lSC}] coordinate (H);
		\path[3d/project={(H) on lSB}] coordinate (K);	
		\path[overlay,3d coordinate={(K')=(H)-(K)x(S)-(K)},
		3d coordinate={(K'')=(K)+(K')},
		3d coordinate={(N)=(H)-(K)}];
		\path[3d/define orthonormal dreibein={A={(K)},B={(S)},C={(K'')}}];
		\pgfmathsetmacro{\R}{sqrt(TD("(K)-(S)o(K)-(S)")}
		\pgfmathsetmacro{\r}{sqrt(TD("(A)-(H)o(A)-(H)")}
		\pgfmathsetmacro{\h}{sqrt(TD("(K)-(H)o(K)-(H)")}
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
			\path (K) pic{3d/frustum={R=\R,r=\r,h=\h}};
			\fill (-upper base) circle[radius=1pt];
		\end{scope}
		\tikzset{3d/.cd,
		plane with normal={(N) through (H) named pU},
		line through={(B) and (C) named lBC}}
		\path[3d/intersection of={lBC with pU}] coordinate (B');
		%
		\pgfmathsetmacro{\myN}{TD("(N)")}
		\pgfmathsetmacro{\ltest}{screendepth(\myN)}
		\ifdim\ltest pt<0pt
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
		  \clip (H) circle[radius=\r];
		  \draw[hidden] (A) -- (C) -- (H) -- cycle (C)--(B')  ;
		\end{scope}
		\begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
		  \clip (H) circle[radius=\r] [generous outside path'];
		  \draw[visible] (A) -- (C) -- (H) -- cycle (C)--(B')  ;
		\end{scope}
		 \draw[hidden]  (B) -- (B') 
		  (A) -- (S) -- (H) -- (K) -- (S) ;   	
		 \draw[visible] (S) -- (K) -- (B);
		\else
		 \draw[visible] (A) -- (C) -- (H) -- cycle
		  (C)--(B')  ;
		 \draw[hidden]  (K) --  (B) -- (B') 
		  (A) -- (S) -- (H) -- (K) -- (S) ;   	
		\fi 
		\foreach \v/\position in 
		{B/below,C/right,A/left,S/above,K/above,H/right} {\draw[draw =black, fill=black] (\v) circle (1.3pt) node [\position=0.2mm] {$\v$}; 
		} 		
	\end{tikzpicture}} 
\end{document}
```
![ani.gif](/image?hash=e3c7a6c51b29ca8668c6521ccb42bf00eec9719c892fe15beee44b01d3f96875)