Polygon is intersection of a plane and a pyramid. - TeX

TopAnswers TeX

Meta

Databases

TeX

Code Golf

APL

C++

.net

db<>fiddle

Java

*nix

PHP

PowerShell

Python

Rust

टेक्-मराठी

Typst

Web Client Dev

Web Server Dev

Polygon is intersection of a plane and a pyramid.

add tag

Anonymous 1123

Let be given a tetrahedron `COAB`. `M`, `N` be two points lies on segments `CO`, `CA`; `P` is inside triagle `OAB`. I want to find intersection of the plane `MNP` and tetrahedron `COAB` like this picture
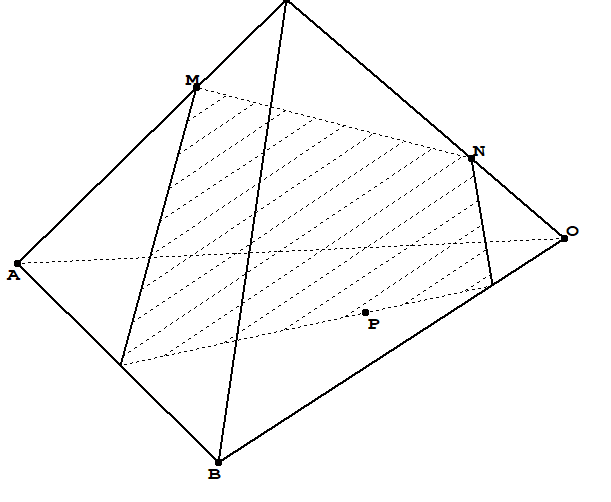
![ScreenHunter 892.png](/image?hash=ce35621b85961e5d61af94d882f34c62d242ef21ffa25d59122bf3f2f25b8f30) 
I tried
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usepackage{fouriernc}
\usetikzlibrary{patterns.meta}
\usetikzlibrary{3dtools,intersections,calc}
\begin{document}
	\tdplotsetmaincoords{70}{80}
	\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round,declare function={a = 1/3;b = 2/3;}]
		\path
		(0,0,0) coordinate (O)
		(0,5,0) coordinate (A)
		(0,3,-3) coordinate (B) 
		(3/2,3,5) coordinate (C)
		[3d coordinate = {(M) = b*(O) - b*(C) + (C)}, 
		3d coordinate = {(N) = a*(A)  - a *(C) + (C)},
		3d coordinate = {(P) = 0.33333*(A)  +  0.3333333*(B) + 0.3333*(O)}] ;
		\path[3d/line through={(O) and (A) named lOA}];
			\path[3d/line through={(O) and (B) named lOB}];
		\path[3d/line through={(A) and (B) named lAB}];
		\path[3d/plane through=(M) and (N) and (P) named pMNP];
		\path[3d/intersection of={lOA with pMNP}] coordinate (Q);
		\path[3d/intersection of={lAB with pMNP}] coordinate (R);
		\path[3d/intersection of={lOB with pMNP}] coordinate (S);
		\foreach \p in {O,A,B,C,M,N,P,Q,R,S}
		\draw[fill=black] (\p) circle (1pt);
				\foreach \p/\g in {O/90,A/90,B/90,C/90,M/90,N/90,P/90,Q/30,R/90,S/90}
		\path (\p)+(\g:3mm) node{$\p$};
		\draw (C) -- (O) -- (B) -- (A) -- cycle (C) - - (B) (M) -- (S) (R) -- (N);
		\draw[dashed] (O) -- (A);
		\draw[pattern={Lines[angle=45]}]  (M) -- (N) -- (R) -- (S) -- cycle;
	\end{tikzpicture}
\end{document} 
```
How to choose the option of the point `P` randomly inside the triale `OAB` (to get a nice view) and how to get dashed lines `MN` and `SR`?

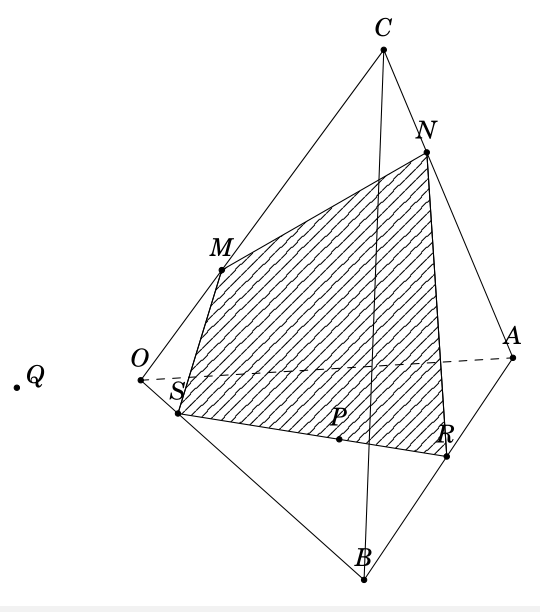
![ScreenHunter 893.png](/image?hash=30171290539e597495ae3e8fee775684d5c2b3c81d6fe21913f7604da818c79d)

PS. When I used `declare function={a = 1/2;b = 1/2;}`, the line `OA` is parallel to the plane `MNP`. I still get the point `Q`.
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usepackage{fouriernc}
\usetikzlibrary{patterns.meta}
\usetikzlibrary{3dtools,intersections,calc}
\begin{document}
	\tdplotsetmaincoords{70}{80}
	\begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round,declare function={a = 1/2;b = 1/2;}]
		\path
		(0,0,0) coordinate (O)
		(0,5,0) coordinate (A)
		(0,3,-3) coordinate (B) 
		(3/2,3,5) coordinate (C)
		[3d coordinate = {(M) = b*(O) - b*(C) + (C)}, 
		3d coordinate = {(N) = a*(A)  - a *(C) + (C)},
		3d coordinate = {(P) = 0.33333*(A)  +  0.3333333*(B) + 0.3333*(O)}] ;
		\path[3d/line through={(O) and (A) named lOA}];
			\path[3d/line through={(O) and (B) named lOB}];
		\path[3d/line through={(A) and (B) named lAB}];
		\path[3d/plane through=(M) and (N) and (P) named pMNP];
		\path[3d/intersection of={lOA with pMNP}] coordinate (Q);
		\path[3d/intersection of={lAB with pMNP}] coordinate (R);
		\path[3d/intersection of={lOB with pMNP}] coordinate (S);
		\foreach \p in {O,A,B,C,M,N,P,Q,R,S}
		\draw[fill=black] (\p) circle (1pt);
				\foreach \p/\g in {O/90,A/90,B/90,C/90,M/90,N/90,P/90,Q/30,R/90,S/90}
		\path (\p)+(\g:3mm) node{$\p$};
		\draw (C) -- (O) -- (B) -- (A) -- cycle (C) - - (B) (M) -- (S) (R) -- (N);
		\draw[dashed] (O) -- (A);
		\draw[pattern={Lines[angle=45]}]  (M) -- (N) -- (R) -- (S) -- cycle;
	\end{tikzpicture}
\end{document} ```

Top Answer

user 3.14159

You already did all the hard work. All I did was to randomize the position of `P`. To see how that works, consider first a parallelogram spanned by `(e1)=(A)-(O)` and `(e2)=(B)-(O)`. A random point is then given by `(P)=(O)+rA*(e1)+rB*(e2)`. For a triangle we need to mirror any point with `rA+rB>1` at the line `(A)--(B)`. 
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usepackage{fouriernc}
\usetikzlibrary{patterns.meta}
\usetikzlibrary{3dtools,intersections,calc}
\begin{document}
\foreach \X in {1,...,20}
{\tdplotsetmaincoords{70}{80}
\begin{tikzpicture}[scale=1,tdplot_main_coords,line join=round, 
	line cap=round,declare function={a=1/3;b=2/3;}]
	\pgfmathsetseed{\X}
	\pgfmathsetmacro{\rndA}{rnd}
	\pgfmathsetmacro{\rndB}{rnd}
	\pgfmathtruncatemacro{\itest}{(\rndA+\rndB>1)}
	\ifnum\itest=1
	 \edef\tmp{\rndA}
	 \pgfmathsetmacro{\rndA}{1-\rndB}
	 \pgfmathsetmacro{\rndB}{1-\tmp}
	\fi
	\path
	(0,0,0) coordinate (O)
	(0,5,0) coordinate (A)
	(0,3,-3) coordinate (B) 
	(3/2,3,5) coordinate (C)
	[3d coordinate={(M)=b*(O) - b*(C) + (C)}, 
	3d coordinate={(N)=a*(A)  - a *(C) + (C)},
	3d coordinate={(P)=(O)+\rndA*(A)-\rndA*(O)+\rndB*(B)-\rndB*(O)}] ;
	\path[3d/line through={(O) and (A) named lOA}];
	\path[3d/line through={(O) and (B) named lOB}];
	\path[3d/line through={(A) and (B) named lAB}];
	\path[3d/plane through=(M) and (N) and (P) named pMNP];
	\path[3d/intersection of={lOA with pMNP}] coordinate (Q);
	\path[3d/intersection of={lAB with pMNP}] coordinate (R);
	\path[3d/intersection of={lOB with pMNP}] coordinate (S);
	\foreach \p in {O,A,B,C,M,N,P,Q,R,S}
	\draw[fill=black] (\p) circle (1pt);
			\foreach \p/\g in {O/90,A/90,B/90,C/90,M/90,N/90,P/90,Q/30,R/90,S/90}
	\path (\p)+(\g:3mm) node{$\p$};
	\draw (C) -- (O) -- (B) -- (A) -- cycle (C) - - (B) (M) -- (S) (R) -- (N);
	\draw[dashed] (O) -- (A);
	\path[pattern={Lines[angle=45]}]  (M) -- (N) -- (R) -- (S) -- cycle;
	\path[dashed] (M) edge (N) (S) edge (R);
\end{tikzpicture}}
\end{document} 
```
![ani.gif](/image?hash=24f1f7b60e35225104422eabdf1c9f2c361b74e94d01c7c98fd74da6ad52ce01)

BTW, I was updating the `3dtools` library for the cone (but am not yet done), so there is a chance the above does not work with the older version (but I do not think so). If this happens, please let me know, then I will upload an intermediate version to GitHub.

I think the simplest possibility would be to use a `3d/polyhedron`, and to just use `fill=none`. But let's do these tests ourselves. All we need to do is to compute the outward-pointing normals on the surfaces, and to then use the sign of its screen depth to decide the visibility of the boundaries and edges embedded in the planes. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{patterns.meta} \usetikzlibrary{3dtools,intersections,calc} \begin{document} \foreach \Angle in {5,10,...,355} {\tdplotsetmaincoords{60}{\Angle} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={a = 5;b = 8;h=5;}] \path (0,0,0) coordinate (A) (a,0,0) coordinate (B) (a,b,0) coordinate (C) (0,b,0) coordinate (D) (0,0,h) coordinate (S) [3d coordinate = {(M) = 0.5*(C) + 0.5*(D)}, 3d coordinate = {(Q) = 0.333*(A) + 0.333*(D) + 0.333*(S)}, 3d coordinate = {(P) = 0.333*(A) + 0.333*(B) + 0.333*(S)}] ; \path[3d/plane through=(M) and (P) and (Q) named pMPQ]; \path[3d/line through={(S) and (A) named lSA}]; \path[3d/line through={(S) and (B) named lSB}]; \path[3d/line through={(S) and (C) named lSC}]; \path[3d/line through={(S) and (D) named lSD}]; \path[3d/line through={(B) and (C) named lBC}]; \path[3d/intersection of={lSA with pMPQ}] coordinate (E); \path[3d/intersection of={lSB with pMPQ}] coordinate (F); \path[3d/intersection of={lSC with pMPQ}] coordinate (G); \path[3d/intersection of={lSD with pMPQ}] coordinate (H); \path[3d/intersection of={lBC with pMPQ}] coordinate (K); \foreach \p in {A,B,C,D,M,P,Q,E,F,G,H,S,K} {\draw[fill=black] (\p) circle (1pt);} \foreach \p/\g in {A/90,B/90,C/90,D/90,M/90,P/90,Q/90,E/90,F/0,G/0,H/0,S/0,K/0} {\path (\p)+(\g:3mm) node{$\p$};} \path[pattern={Lines[angle=45]}] (E) -- (F) -- (K) -- (M) -- (H) -- cycle; \path[dashed] (K) edge (M); \foreach \X/\Y in {(B)-(C)x(B)-(S)/(B)--(C)--(S)--cycle (K)edge(F), (A)-(B)x(B)-(S)/(A)--(B)--(S)--cycle (E)edge(F), (D)-(A)x(A)-(S)/(A)--(D)--(S)--cycle (E)edge(H), (C)-(D)x(D)-(S)/(C)--(D)--(S)--cycle (M)edge(H) } {\pgfmathsetmacro{\myn}{TD("\X")} \pgfmathtruncatemacro{\itest}{(screendepth(\myn)>0?1:0)} \ifnum\itest>0 \draw[3d/visible] \Y; \else \draw[3d/hidden] \Y; \fi } \path (current bounding box.north west) node[below right]{$Angle=\Angle^\circ$}; \end{tikzpicture}} \end{document} ```

@marmot, re: [your answer](#a1712), Please help me to draw dashed lines automatically in this code. I do not know how to put `\pgfmathtruncatemacro{\itest}`. My code ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{patterns.meta} \usetikzlibrary{3dtools,intersections,calc} \begin{document} \foreach \Angle in {5,10,...,355} {\tdplotsetmaincoords{60}{\Angle} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round, declare function={a = 5;b = 8;h=5;}] \path (0,0,0) coordinate (A) (a,0,0) coordinate (B) (a,b,0) coordinate (C) (0,b,0) coordinate (D) (0,0,h) coordinate (S) [3d coordinate = {(M) = 0.5*(C) + 0.5*(D)}, 3d coordinate = {(Q) = 0.333*(A) + 0.333*(D) + 0.333*(S)}, 3d coordinate = {(P) = 0.333*(A) + 0.333*(B) + 0.333*(S)}] ; \path[3d/plane through=(M) and (P) and (Q) named pMPQ]; \path[3d/line through={(S) and (A) named lSA}]; \path[3d/line through={(S) and (B) named lSB}]; \path[3d/line through={(S) and (C) named lSC}]; \path[3d/line through={(S) and (D) named lSD}]; \path[3d/line through={(B) and (C) named lBC}]; \path[3d/intersection of={lSA with pMPQ}] coordinate (E); \path[3d/intersection of={lSB with pMPQ}] coordinate (F); \path[3d/intersection of={lSC with pMPQ}] coordinate (G); \path[3d/intersection of={lSD with pMPQ}] coordinate (H); \path[3d/intersection of={lBC with pMPQ}] coordinate (K); \foreach \p in {A,B,C,D,M,P,Q,E,F,G,H,S,K} \draw[fill=black] (\p) circle (1pt); \foreach \p/\g in {A/90,B/90,C/90,D/90,M/90,P/90,Q/90,E/90,F/0,G/0,H/0,S/0,K/0} \path (\p)+(\g:3mm) node{$\p$}; \path[pattern={Lines[angle=45]}] (E) -- (F) -- (K) -- (M) -- (H) -- cycle; \path[dashed] (E) edge (F) (K) edge (M) (H) edge (E); \path[solid] (M) edge (H) (F) edge (K); \draw [dashed] (S) -- (A) (A) -- (B) (A) -- (D); \draw (S) -- (B) -- (C) -- (D) -- (S) (S) -- (C); \path (current bounding box.north west) node[below right]{$Angle=\Angle^\circ$}; \end{tikzpicture}} \end{document} ```

Yes, this works. Maybe one day I have the passion to improve the parser. There is always a risk of breaking things. In an ideal world one could set up something like `tikzmath`. I had a look into this but there are many obstacles. For instance, one cannot add `fpu` easily but for 3d operations we need it often.

It is the same issue as previously. The parser is not too sophisticated. When it sees a `(` it thinks it is a coordinate. So you cannot have `(1-k)*k`. Once you fix that, it works. ```` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usepackage{fouriernc} \usetikzlibrary{patterns.meta} \usetikzlibrary{3dtools,intersections,calc} \begin{document} \tdplotsetmaincoords{70}{80} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round,declare function={a = 1/3;b = 2/3;k=1/3;t=2/5; kp=k*(1-k);}] \path (0,0,0) coordinate (O) (0,5,0) coordinate (A) (0,3,-2) coordinate (B) (3,3,5) coordinate (C) [3d coordinate = {(M) = b*(O) - b*(C) + (C)}, 3d coordinate = {(N) = a*(A) - a *(C) + (C)}, 3d coordinate = {(H) =k*(A) + kp*(B)}]; \pgfmathsetmacro{\mybarycenter}{barycenter("(A),(B),(O)")} \path (\mybarycenter) coordinate (P); \path[3d/line through={(O) and (A) named lOA}]; \path[3d/line through={(O) and (B) named lOB}]; \path[3d/line through={(A) and (B) named lAB}]; \path[3d/plane through=(M) and (N) and (P) named pMNP]; \path[3d/intersection of={lOA with pMNP}] coordinate (Q); \path[3d/intersection of={lAB with pMNP}] coordinate (R); \path[3d/intersection of={lOB with pMNP}] coordinate (S); \foreach \p in {O,A,B,C,M,N,P,Q,R,S} \draw[fill=black] (\p) circle (1pt); \foreach \p/\g in {O/90,A/90,B/90,C/90,M/90,N/90,P/90,Q/30,R/90,S/90} \path (\p)+(\g:3mm) node{$\p$}; \draw (C) -- (O) -- (B) -- (A) -- cycle (C) - - (B) ; \draw[dashed] (O) -- (A); \path[pattern={Lines[angle=45]}] (M) -- (N) -- (R) -- (S) -- cycle; \path[dashed] (M) edge (N) (S) edge (R); \path[solid] (M) edge (S) (N) edge (R); \path pic[red,dashed]{3d incircle={% A={(A)},B={(B)},C={(O)},center name=I}}; \path pic[blue]{3d incircle={% A={(O)},B={(B)},C={(C)},center name=J}}; \path pic[green]{3d incircle={% A={(A)},B={(O)},C={(C)},center name=T}}; \path pic[thick,orange]{3d incircle={% A={(A)},B={(B)},C={(C)},center name=X}}; \end{tikzpicture} \end{document} ```

Full code ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usepackage{fouriernc} \usetikzlibrary{patterns.meta} \usetikzlibrary{3dtools,intersections,calc} \begin{document} \tdplotsetmaincoords{70}{80} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join = round, line cap = round,declare function={a = 1/3;b = 2/3;k=1/3;t=2/5;}] \path (0,0,0) coordinate (O) (0,5,0) coordinate (A) (0,3,-2) coordinate (B) (3,3,5) coordinate (C) [3d coordinate = {(M) = b*(O) - b*(C) + (C)}, 3d coordinate = {(N) = a*(A) - a *(C) + (C)}, 3d coordinate = {(H) =k*(A) + (1-k)*k*(B)}]; \pgfmathsetmacro{\mybarycenter}{barycenter("(A),(B),(O)")} \path (\mybarycenter) coordinate (P); \path[3d/line through={(O) and (A) named lOA}]; \path[3d/line through={(O) and (B) named lOB}]; \path[3d/line through={(A) and (B) named lAB}]; \path[3d/plane through=(M) and (N) and (P) named pMNP]; \path[3d/intersection of={lOA with pMNP}] coordinate (Q); \path[3d/intersection of={lAB with pMNP}] coordinate (R); \path[3d/intersection of={lOB with pMNP}] coordinate (S); \foreach \p in {O,A,B,C,M,N,P,Q,R,S} \draw[fill=black] (\p) circle (1pt); \foreach \p/\g in {O/90,A/90,B/90,C/90,M/90,N/90,P/90,Q/30,R/90,S/90} \path (\p)+(\g:3mm) node{$\p$}; \draw (C) -- (O) -- (B) -- (A) -- cycle (C) - - (B) ; \draw[dashed] (O) -- (A); \path[pattern={Lines[angle=45]}] (M) -- (N) -- (R) -- (S) -- cycle; \path[dashed] (M) edge (N) (S) edge (R); \path[solid] (M) edge (S) (N) edge (R); \path pic[red,dashed]{3d incircle={% A={(A)},B={(B)},C={(O)},center name=I}}; \path pic[blue]{3d incircle={% A={(O)},B={(B)},C={(C)},center name=J}}; \path pic[green]{3d incircle={% A={(A)},B={(O)},C={(C)},center name=T}}; \path pic[thick,orange]{3d incircle={% A={(A)},B={(B)},C={(C)},center name=X}}; \end{tikzpicture}\end{document} ```

I added ``` \ifnum\month>10\relax \typeout{Hibernation season has just started.}% \fi \ifnum\month<5\relax \typeout{Hibernation season has not yet ended.}% \fi \ifnum\month=2\relax \ifnum\day=2 \typeout{Yay! Groundhog Day!}% \fi \fi ``` In a way this makes use of the fact that there are (to my knowledge) no marmots on the southern hemisphere.

Or just look up how `halloweenmath` is doing it. ``` \DeclareOption{boo-10-31}{% \ifnum\month=10 \ifnum\day=31 \let \@HwM@opt@say@BOO \@HwM@say@BOO \else \let \@HwM@opt@say@BOO \@empty \fi \else \let \@HwM@opt@say@BOO \@empty \fi } ``` This looks straightforward enough.

I was using TL2020. Do you use the latest version of [3dtools](https://github.com/marmotghost/tikz-3dtools)? It contains `\typeout{The plane and line do not intersect within the uncertainties.}`. Maybe `\typeout` is not the right command but on my Mac it types it out to the console.

They are almost in. Note that, like the circumcenter, the orthocenter nor may not be inside the triangle. In the following code, `I` is the circumcenter, `M` is the barycenter and `Q` is the orthocenter. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} \begin{document} \tdplotsetmaincoords{70}{80} \begin{tikzpicture}[scale=1,tdplot_main_coords,line join=round, line cap=round,c/.style={circle,inner sep=1.2pt,fill}] \draw (0,0,0) coordinate (O) (0,5,0) coordinate (A) -- (0,3,3) coordinate (B) -- (3/2,1,1) coordinate (C) -- cycle; \path[3d/circumcircle center] coordinate (I); \pgfmathsetmacro{\mybarycenter}{barycenter("(A),(B),(C)")} \path (\mybarycenter) coordinate (M) [3d coordinate={(Q)=-2*(I)+(A)+(B)+(C)}]; \path foreach \p in {O,A,B,C,I,M,Q} {(\p) node[c,label=above:{$\p$}]{}}; \end{tikzpicture} \end{document} ``` ![Screen Shot 2020-11-01 at 9.35.04 PM.png](/image?hash=d1b81719e3e09cd7475638e2b4dc2758992d78d798cf2786a3ee0b920176113b)

@Anonymous, re: [your question](#question), a quick comment: for `a=1/2;b=1/2;` I get the message > The plane and line do not intersect within the uncertainties. and the code returns the origin, i.e. `Q` is at `O`.

1 Answer