Is this code true about a cube is insribed a cylinder?
tikz add tag
Anonymous 1123 
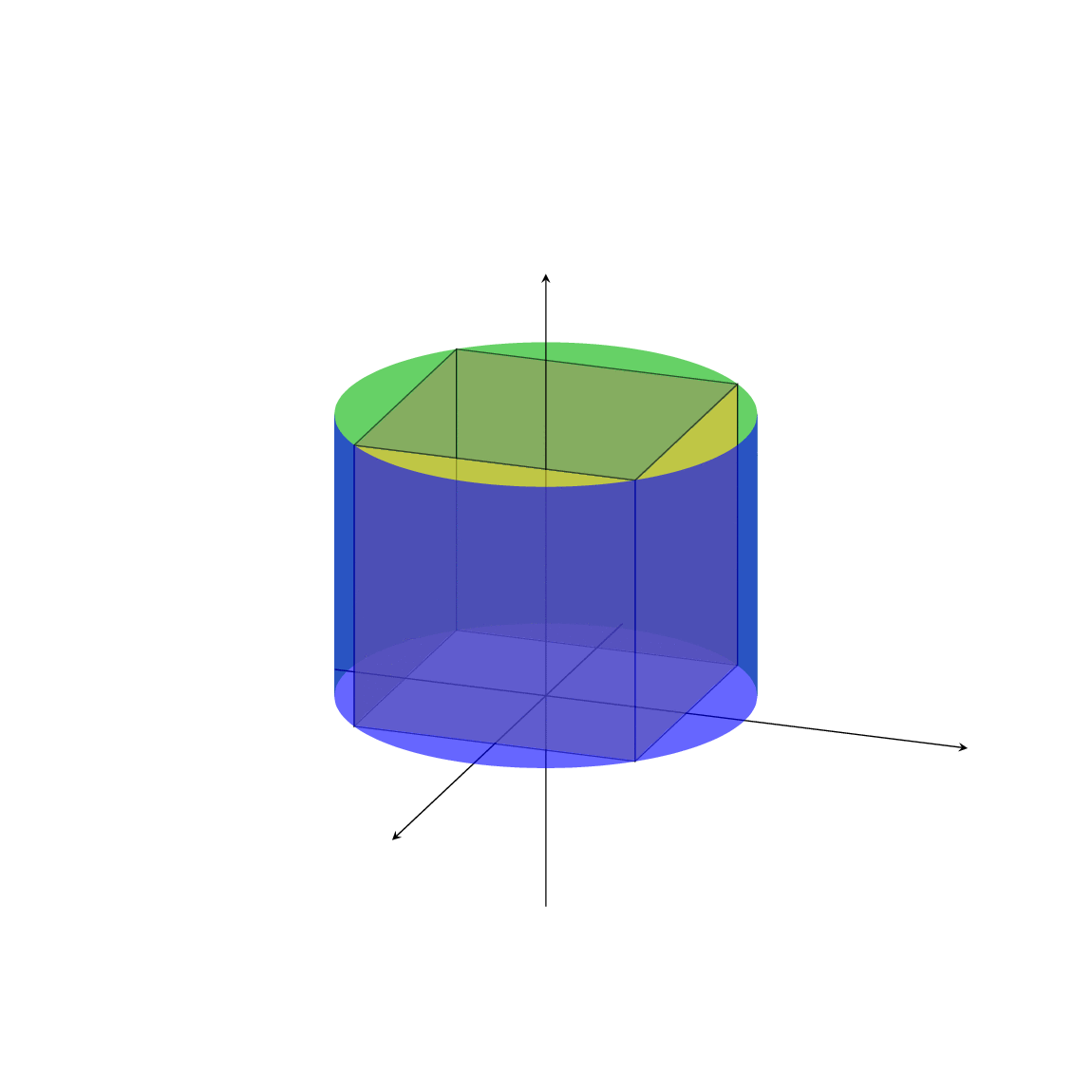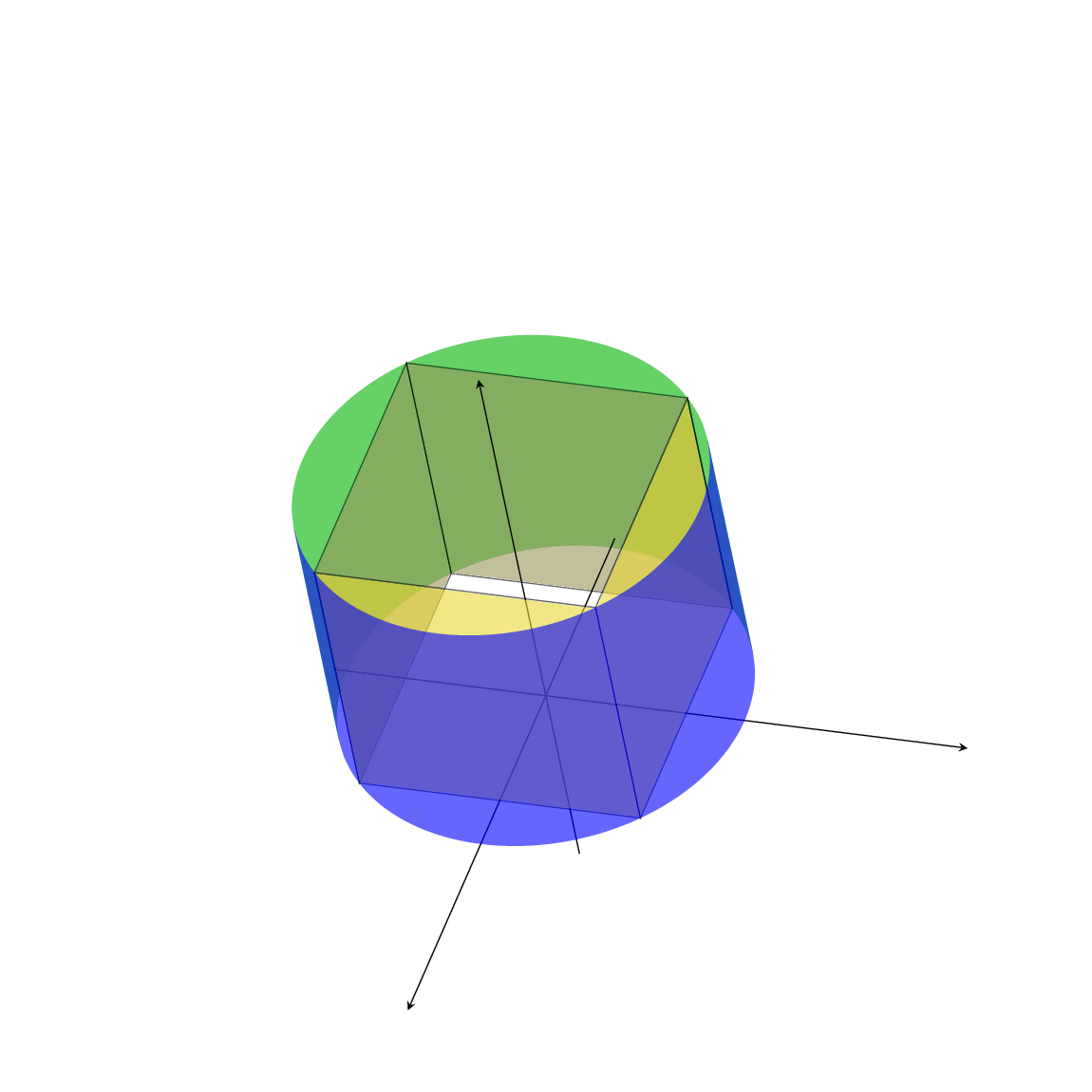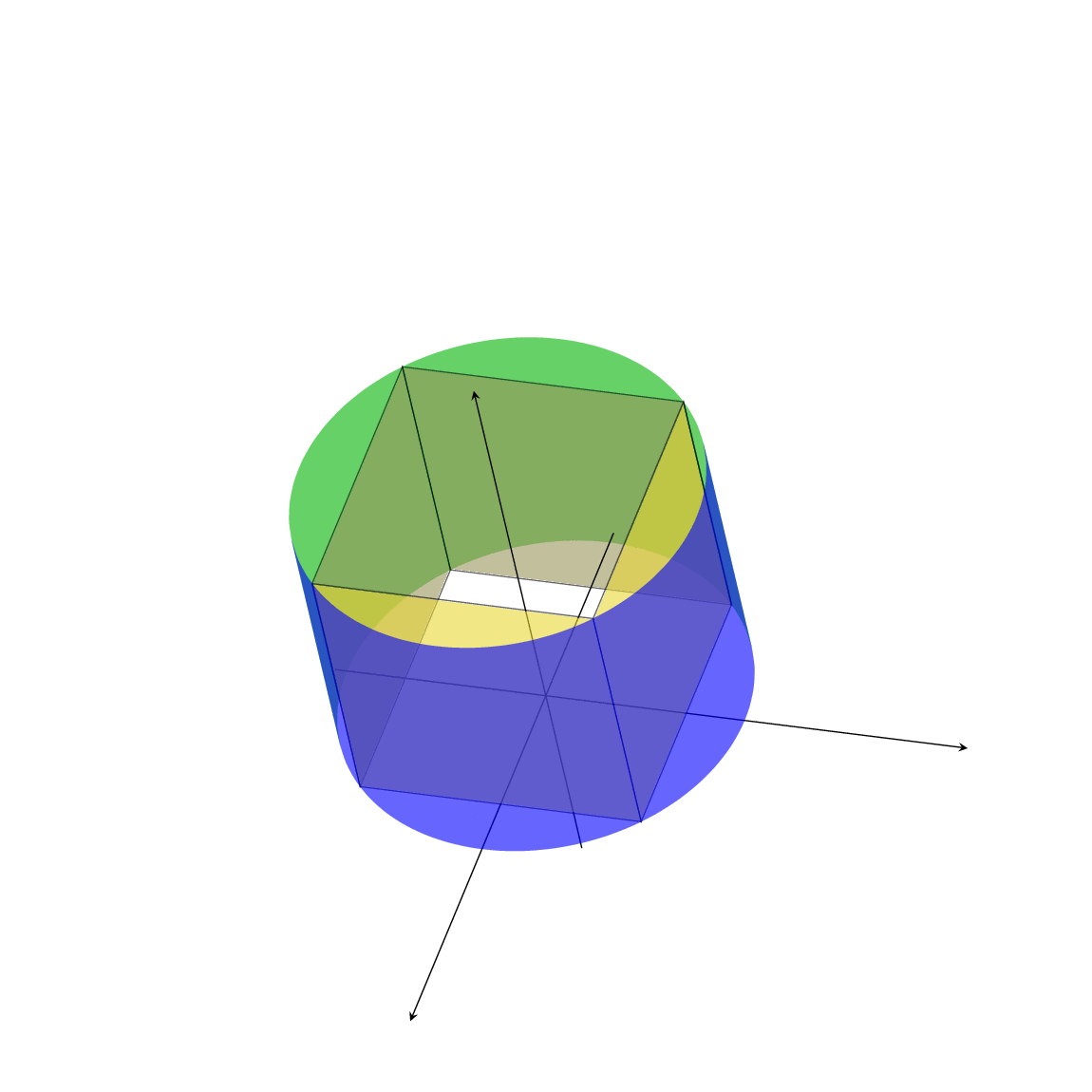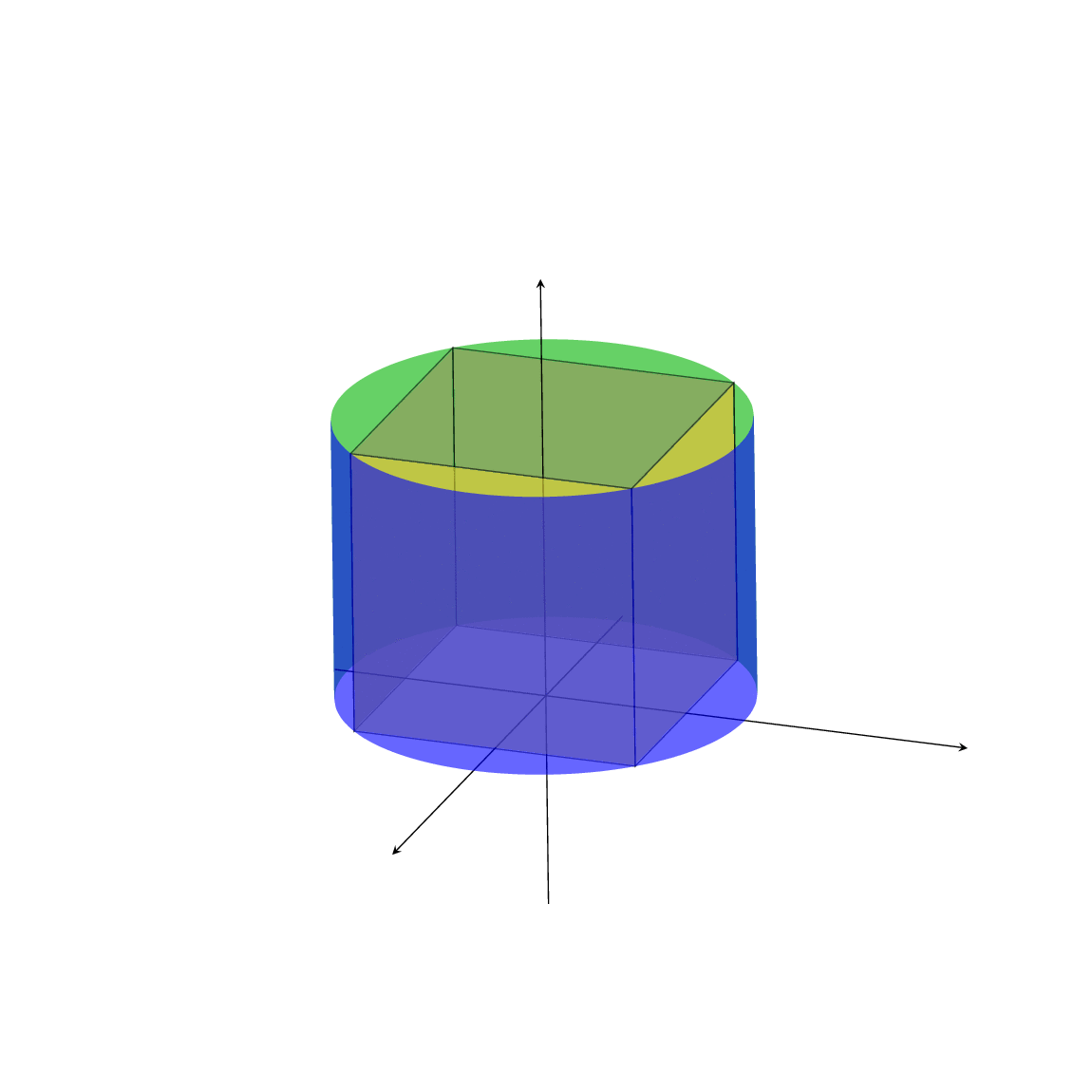
This is not my code, I copied at [here](https://www.facebook.com/groups/toanvalatex/) I do not understand all code. I do not see the author uses `\tdplotmainphi` or `\tdplotmaintheta` to draw cylinder. Is this code true?
```
\documentclass[tikz,border=5mm]{standalone}
%\usepackage{tikz}
\usepackage{tikz-3dplot}
\usepackage{ifthen}
\usetikzlibrary{shadows,calc,fadings,shadings}
\pagecolor{yellow!35}
\begin{document}
	\foreach \m in{80,79,...,31,30,31,...,80}{
		\ifthenelse{\m>30}{
			\def\l{70}
			\begin{tikzpicture}
				\tdplotsetmaincoords{\m}{70}
				\pgfmathsetmacro{\k}{\l+180}
				\clip (-6,-5)rectangle(10,10);
				\begin{scope}[line join=bevel,tdplot_main_coords]
					\clip(0,0,0)circle(9cm);
					\draw[cyan](0,0,4)circle(4);
					\tikzset{cylinder/.pic={
							\fill [samples=100,green, fill opacity = 3/5,domain=0:360]plot ({4*cos(\x)},{4*sin(\x)},0);
							\fill[orange](-4,0,0)--(0,4,0)--(4,0,0)--(4,0,0)--(0,-4,0);
						}
					}
					\path(0,0,0)pic{cylinder};
					\fill[upper right=cyan, upper left =green,lower left = cyan,lower right =green,opacity=2/5]plot [samples=100,domain={180+\k}:{360+\k}]({4*cos(\x)},{4*sin(\x)},0)--plot [samples=100,domain={360+\k}:{\k+180}]({4*cos(\x)},{4*sin(\x)},4);
					\draw[red](0,-4,0)--(0,4,0);
					\draw[red](0,4,0)--(0,8,0);
					\draw[red](-4,0,0)--(4,0,0);
					\fill[violet,opacity=0.5](-4,0,0)--(0,4,0)--(0,4,4)--(-4,0,4)--cycle;
					\draw[blue,->](0,0,4)--(0,0,8);
					\fill[red,opacity=3/4](4,0,0)--(0,4,0)--(0,4,4)--(4,0,4)--cycle;
					\fill[green,opacity=3/4](4,0,0)--(0,-4,0)--(0,-4,4)--(4,0,4)--cycle;
					\fill[yellow,opacity=3/4](0,-4,0)--(0,-4,4)--(-4,0,4)--(-4,0,0)--cycle;
					\fill[blue,opacity=3/5]plot [samples=100,domain={\k}:{180+\k}]({4*cos(\x)},{4*sin(\x)},0)--plot [samples=100,domain={180+\k}:{\k}]({4*cos(\x)},{4*sin(\x)},4);
					\draw[green](0,0,0)--(0,0,4);
					\draw[green](-4,0,4)--(4,0,4);
					\draw[green](0,-4,4)--(0,4,4)(0,0,4)circle(2pt);
					\draw[red,->](4,0,0)--(8,0,0);
					\draw[red,->](0,4,0)--(0,8,0);
				\end{scope}
		\end{tikzpicture}}
		{
			\foreach \l in{70,71,...,149,150,149,...,70}{
				\begin{tikzpicture}
					\tdplotsetmaincoords{30}{\l}
					\pgfmathsetmacro{\k}{\l+180}
					\clip (-6,-5)rectangle(10,10);
					\begin{scope}[line join=bevel,tdplot_main_coords]
						\draw[cyan](0,0,4)circle(4);
						\tikzset{cylinder/.pic={
								\fill [samples=100,green, fill opacity = 3/5,domain=0:360]plot ({4*cos(\x)},{4*sin(\x)},0);
								\fill[orange](-4,0,0)--(0,4,0)--(4,0,0)--(4,0,0)--(0,-4,0);
							}
						}
						\path(0,0,0)pic{cylinder};
						\fill[upper right=cyan, upper left =green,lower left = cyan,lower right =green,opacity=2/5]plot [samples=100,domain={180+\k}:{360+\k}]({4*cos(\x)},{4*sin(\x)},0)--plot [samples=100,domain={360+\k}:{\k+180}]({4*cos(\x)},{4*sin(\x)},4);
						\draw[red](0,-4,0)--(0,4,0);
						\draw[red](0,4,0)--(0,8,0);
						\draw[red](-4,0,0)--(4,0,0);
						\fill[violet,opacity=0.5](-4,0,0)--(0,4,0)--(0,4,4)--(-4,0,4)--cycle;
						\draw[blue,->](0,0,4)--(0,0,8);
						\fill[red,opacity=3/4](4,0,0)--(0,4,0)--(0,4,4)--(4,0,4)--cycle;
						\fill[green,opacity=3/4](4,0,0)--(0,-4,0)--(0,-4,4)--(4,0,4)--cycle;
						\fill[yellow,opacity=3/4](0,-4,0)--(0,-4,4)--(-4,0,4)--(-4,0,0)--cycle;
						\fill[blue,opacity=3/5]plot [samples=100,domain={\k}:{180+\k}]({4*cos(\x)},{4*sin(\x)},0)--plot [samples=100,domain={180+\k}:{\k}]({4*cos(\x)},{4*sin(\x)},4);
						\draw[green](0,0,0)--(0,0,4);
						\draw[green](-4,0,4)--(4,0,4);
						\draw[green](0,-4,4)--(0,4,4)(0,0,4)circle(2pt);
						\draw[red,->](4,0,0)--(8,0,0);
						\draw[red,->](0,4,0)--(0,8,0);
					\end{scope}
			\end{tikzpicture}}
		}
	}
\end{document}
```
Top Answer
user 3.14159 
As mentioned in the comments, the code does use `\tdplotmainphi`. However, this is actually not necessary. This answer comes with a pic that draws a cyclinder with an arbitrary axis. It also can be rotated by using rotated coordinates. It does not use `\tdplotmainphi` or `\tdplotmaintheta`. It does not rely on the specific way you installed your 3d view. The same statement applies to the polyhedron. So in order to know whether or not a code is correct it is generally not suffcient to check whether it uses certain macros.
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\tikzset{pics/3d/cylinder/.style={code={
 \tikzset{3d/cylinder/.cd,#1}
 \def\pv##1{\pgfkeysvalueof{/tikz/3d/cylinder/##1}}%
 \pgfmathsetmacro{\axisnorm}{TD("\pv{axis}o\pv{axis}")}%
 \ifdim\axisnorm pt<0.01pt\relax
  \typeout{Axis too short.}%
 \else
  \pgfmathsetmacro{\cylinderx}{TD("\pv{axis}x(nscreenx,nscreeny,nscreenz)")}%
  \pgfmathsetmacro{\normcylinderx}{TD("(\cylinderx)o(\cylinderx)")}%
  \ifdim\normcylinderx pt<0.005pt\relax
   % cylinder axis rather parallel to normal on screen
  \else
   \pgfmathsetmacro{\normcylinderx}{1/sqrt(\normcylinderx)}%
   \pgfmathsetmacro{\cylinderx}{TD("\normcylinderx*(\cylinderx)")}%
   \pgfmathsetmacro{\cylindery}{TD("\pv{axis}x(\cylinderx)")}%	 
   \pgfmathtruncatemacro{\itest}{screendepth(\cylindery)<0}%
   \ifnum\itest=1
    \pgfmathsetmacro{\cylindery}{TD("-1*(\cylindery)")}%
   \fi
   \pgfmathsetmacro{\axisnorm}{1/sqrt(\axisnorm)}
   \pgfmathsetmacro{\cylinderz}{TD("\axisnorm*\pv{axis}")}%
   \path[overlay] (\cylinderx) coordinate (cylinderx)
    (\cylindery) coordinate (cylindery)
	(\cylinderz) coordinate (cylinderz);
   \begin{scope}[x={(cylinderx)},y={(cylindery)},z={(cylinderz)}]
	\begin{pgfonlayer}{\pgfkeysvalueof{/tikz/3d/cylinder/back layer}}
	 \path[3d/cylinder/back]
	  plot[variable=\t,domain=-180:0,smooth] 
	  ({\pv{r}*cos(\t)},{\pv{r}*sin(\t)},0)
	  -- plot[variable=\t,domain=0:-180,smooth] 
	  ({\pv{r}*cos(\t)},{\pv{r}*sin(\t)},\pv{h}) -- cycle;
	\end{pgfonlayer}
	\begin{pgfonlayer}{\pgfkeysvalueof{/tikz/3d/cylinder/fore layer}}
	 \path[3d/cylinder/fore]
	  plot[variable=\t,domain=180:0,smooth] 
	  ({\pv{r}*cos(\t)},{\pv{r}*sin(\t)},0)
	  -- plot[variable=\t,domain=0:180,smooth] 
	  ({\pv{r}*cos(\t)},{\pv{r}*sin(\t)},\pv{h}) -- cycle;
	\end{pgfonlayer}
   \end{scope}	
  \fi
 \fi
	}},
	3d/cylinder/.cd,r/.initial=1,h/.initial=1,
	axis/.initial={(0,0,1)},
	back/.style={fill=green!70!black},
	fore/.style={fill=blue},
	back layer/.initial={main},
	fore layer/.initial={main}
	}

\begin{document}
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfdeclarelayer{behind}  
\pgfsetlayers{behind,background,main,foreground}
\foreach \Angle in {0,2,...,40,38,36,...,2}
{\tdplotsetmaincoords{70}{110}
\begin{tikzpicture}[tdplot_main_coords,
	declare function={a=2;h=4;}]
 \path[tdplot_screen_coords,use as bounding box]
 		(-7,-5) rectangle (7,9);
 \tdplotsetrotatedcoords{0}{\Angle}{0}
 \begin{scope}[tdplot_rotated_coords]	
 \path[opacity=0.5] pic{3d/cylinder={r={a*sqrt(2)},h=h,axis={(0,0,1)},
 	fore layer=foreground,back layer=behind,
	back/.style={fill=green!70!black,opacity=0.6},
	fore/.style={fill=blue,opacity=0.6}}};
 \path (-a,-a,0)  coordinate (A)
  (a,-a,0)  coordinate (B)
  (a,a,0)  coordinate (C)
  (-a,a,0)  coordinate (D)
  (-a,-a,h)  coordinate (A')
  (a,-a,h)  coordinate (B')
  (a,a,h)  coordinate (C')
  (-a,a,h)  coordinate (D')
  (0,0,h/2) coordinate (I);
 \draw[-stealth] (-3,0,0) -- (6,0,0);
 \draw[-stealth] (0,-3,0) -- (0,6,0);
 \draw[-stealth] (0,0,-3) -- (0,0,6);
  \tikzset{3d/polyhedron/.cd,O={(I)},
  	   fore/.style={opacity=0.6},fore layer=main,
  	   back/.style={opacity=0.6},back layer=background,
 	   draw face with corners={{(A)},{(B)},{(B')},{(A')}},
 	   draw face with corners={{(B)},{(C)},{(C')},{(B')}},
 	   draw face with corners={{(C)},{(D)},{(D')},{(C')}},
 	   draw face with corners={{(D)},{(A)},{(A')},{(D')}},
 };
 \end{scope}
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=ba2b5f8a7edd2fc82933d2a267ec87ee171df61392c2f6f2436cadf51505fbcd)
comments
transcript

Enter question or answer id or url (and optionally further answer ids/urls from the same question) from

Separate each id/url with a space. No need to list your own answers; they will be imported automatically.