Anonymous 1123
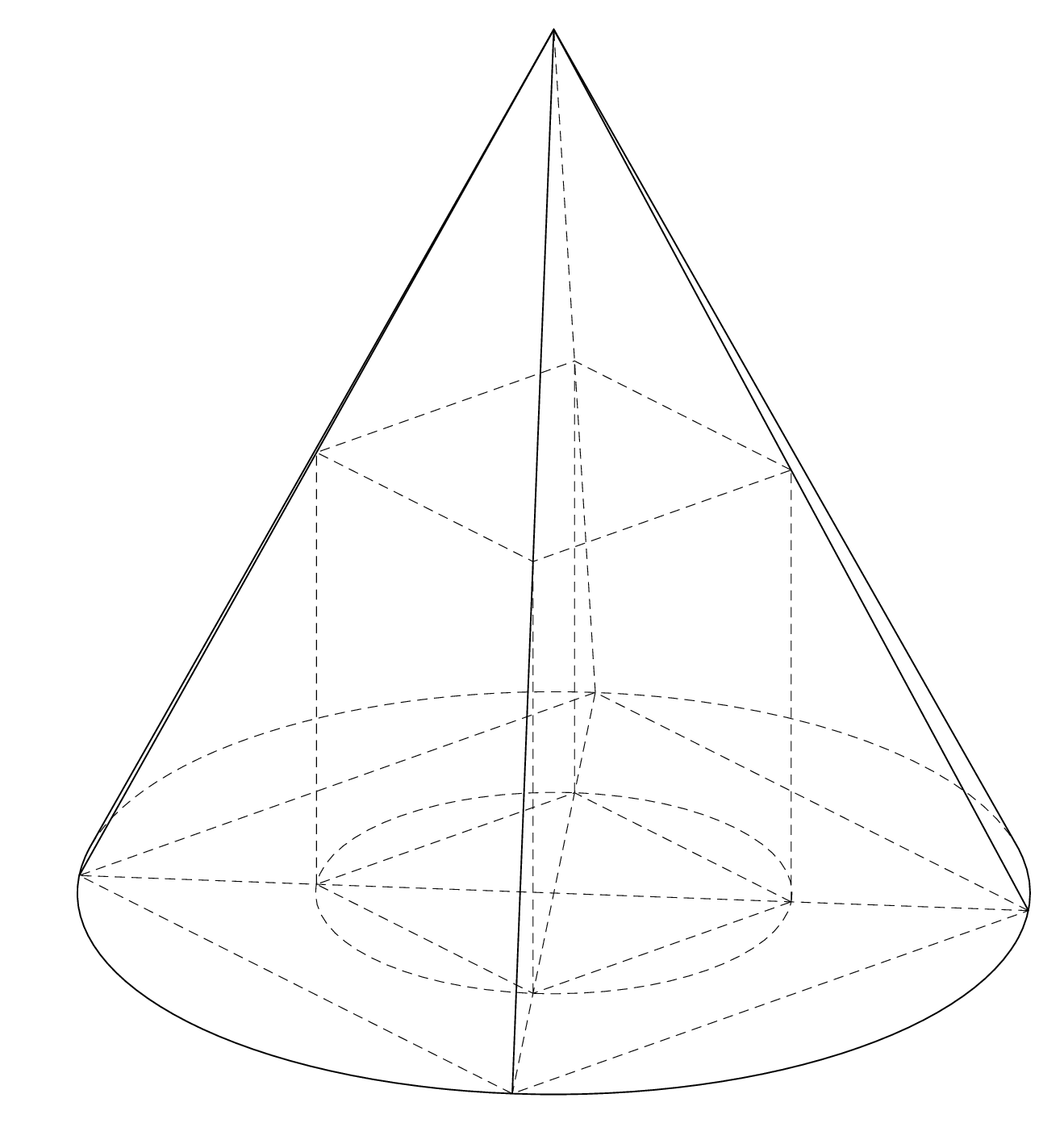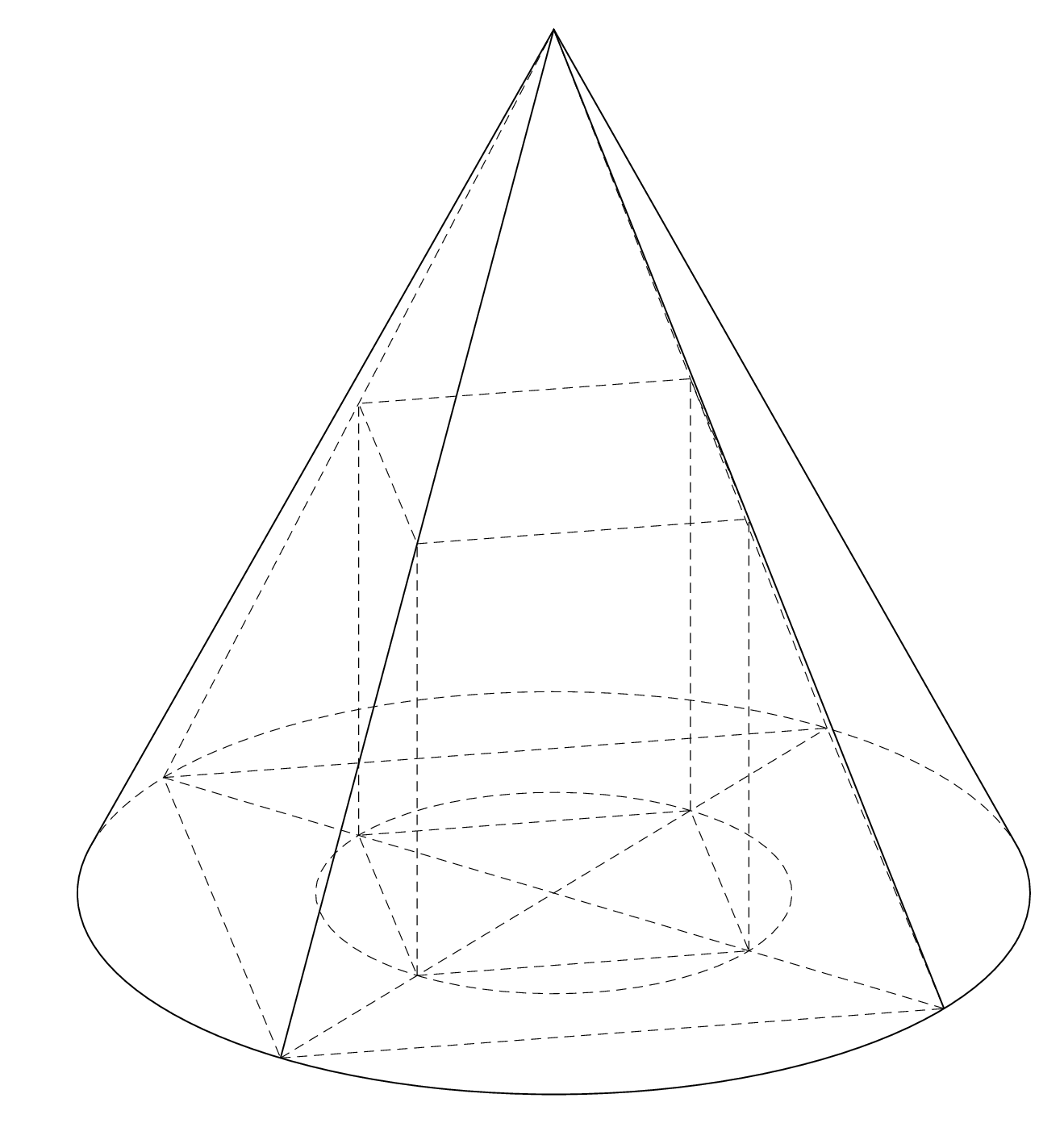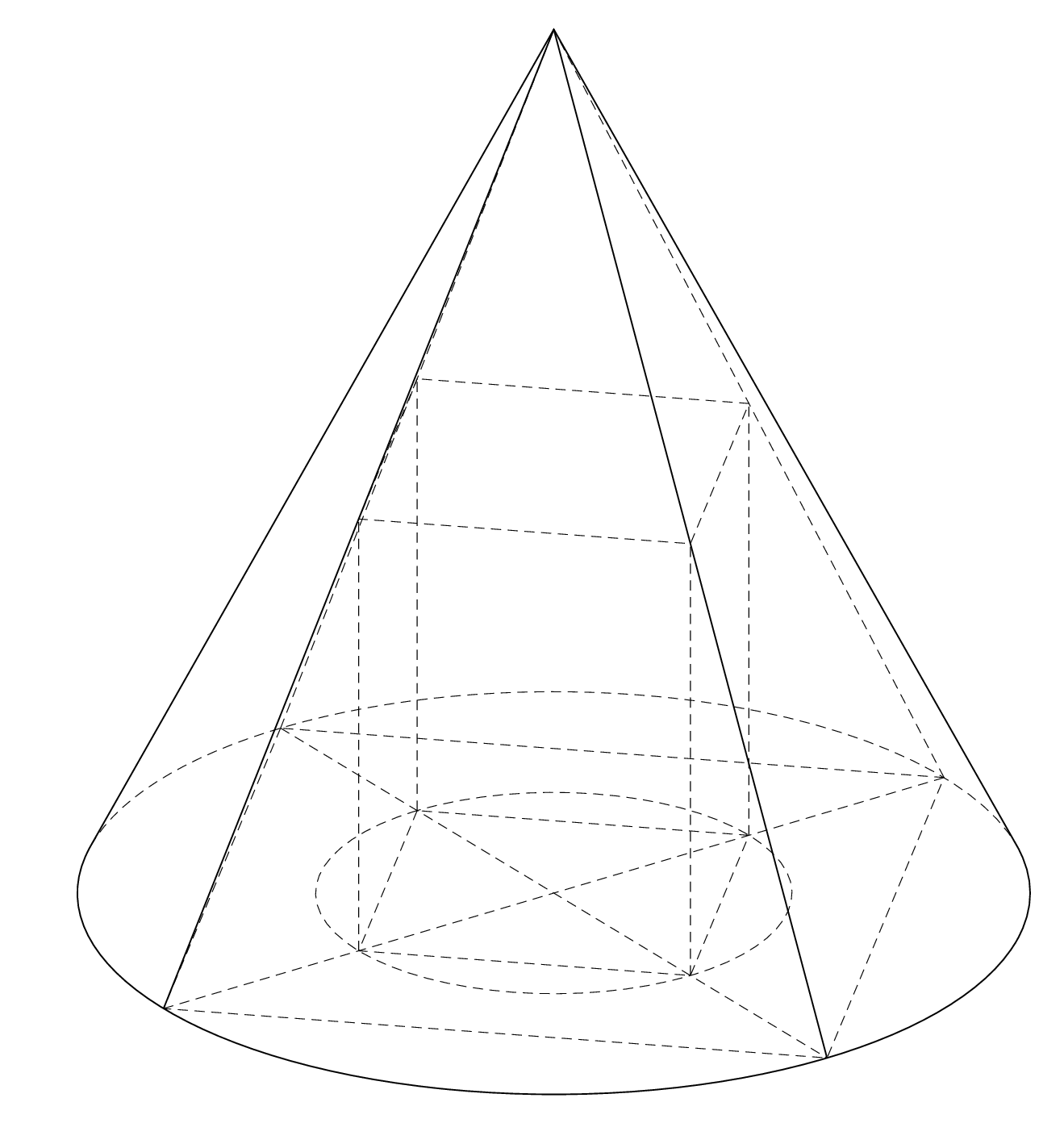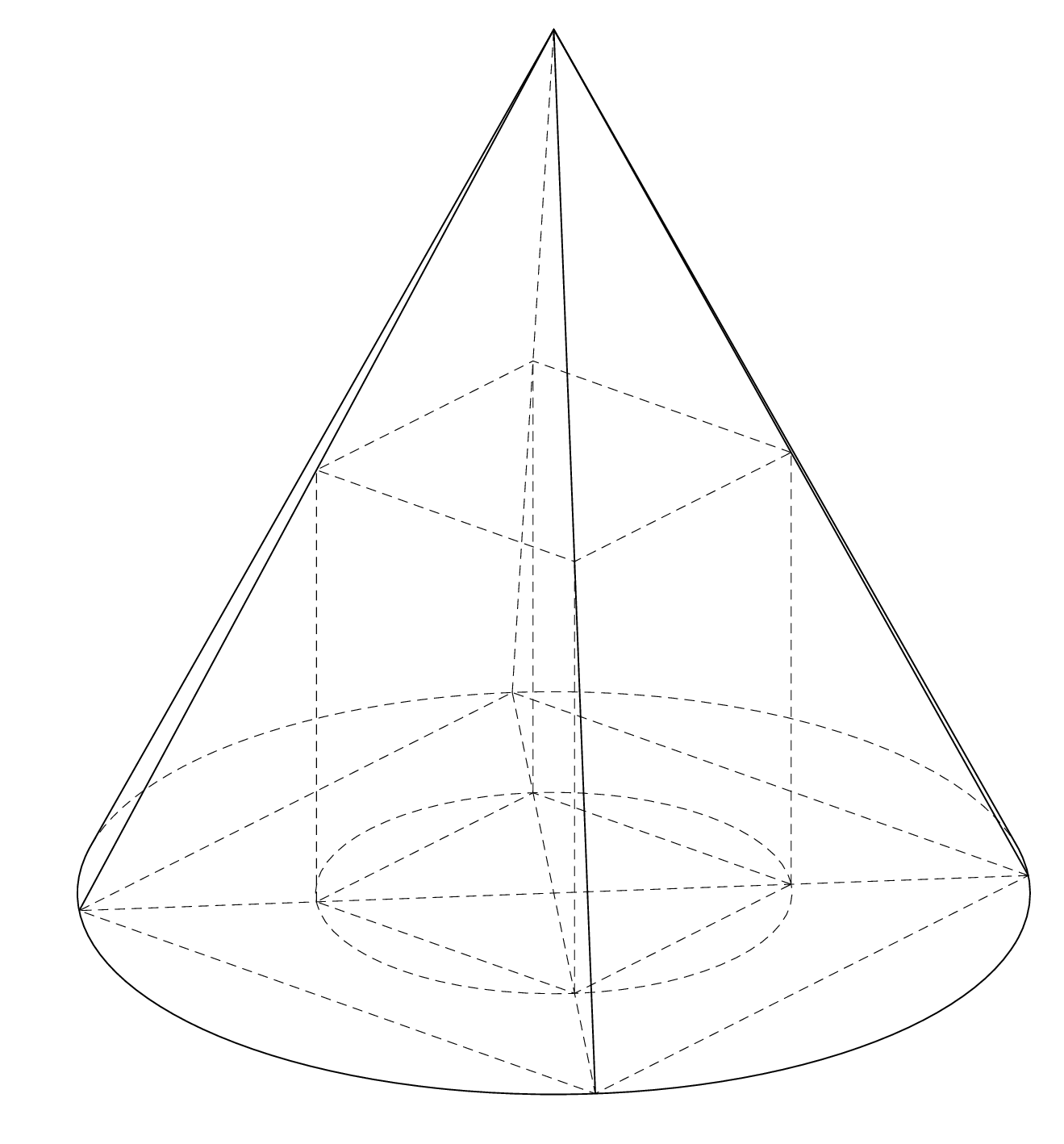
I am trying to draw a rectangular parallelepiped is inscribed in a right circular cone. My code
```
\documentclass[border=2mm,12pt,tikz]{standalone}
\usepackage{fouriernc}
\usepackage{tikz-3dplot}
\usetikzlibrary{calc,backgrounds}
\begin{document}
%polar coordinates of visibility
\pgfmathsetmacro\th{65}
\pgfmathsetmacro\az{110}
\tdplotsetmaincoords{\th}{\az}
%parameters of the cone
\pgfmathsetmacro\R{5} %radius of base
\pgfmathsetmacro\v{2*\R} %hight of cone
\pgfmathsetmacro\a{3}
\pgfmathsetmacro\b{4}
\pgfmathsetmacro\r{{1/2*sqrt(\a*\a+\b*\b)}}
\pgfmathsetmacro\h{(\R-\r)*\v/\R}
\begin{tikzpicture} [scale=0.8, tdplot_main_coords]
\begin{scope}[canvas is xy plane at z=0]
\path
coordinate (O) at (0,0)
coordinate (A) at (\R,0)
coordinate (B) at (0,\R)
coordinate (C) at (-\R,0)
coordinate (D) at (0,-\R,0)
coordinate (M) at (\r,0)
coordinate (N) at (0,\r)
coordinate (P) at (-\r,0)
coordinate (Q) at (0,-\r);
\end{scope}
\begin{scope}[canvas is xy plane at z=\h]
\path coordinate (M') at (\r,0)
coordinate (N') at (0,\r)
coordinate (P') at (-\r,0)
coordinate (Q') at (0,-\r)
;
\end{scope}
\coordinate (S) at (0,0,\v);
\foreach \v/\position in {O/below,A/below, B/right, C/below, D/left, S/above} {\draw[draw =black, fill=black] (\v) circle (1.5pt) node [\position=0.2mm] {$\v$};
}
\foreach \X in {A,B} \draw[thick] (\X) -- (S);
\foreach \X in {M,N,P,Q} \draw[dashed] (\X) -- (\X');
\draw[dashed] (A) -- (B) -- (C) -- (D) -- cycle
(M) -- (N) -- (P) -- (Q) -- cycle
(M') -- (N') -- (P') -- (Q') -- cycle
(A) -- (C) (B) -- (D)
(S)--(O) (S)-- (C);
\foreach \Y in {M, N, P, Q, M', N', P', Q'}
\fill (\Y) circle[radius=1.1pt];
\begin{scope}[canvas is xy plane at z=0]
\draw[dashed] (O) circle[radius=\r];
\end{scope}
\pgfmathsetmacro\cott{{cot(\th)}}
\pgfmathsetmacro\fraction{\R*\cott/\v}
\pgfmathsetmacro\fraction{\fraction<1 ? \fraction : 1}
\pgfmathsetmacro\angle{{acos(\fraction)}}
% % angles for transformed lines
\pgfmathsetmacro\PhiOne{180+(\az-90)+\angle}
\pgfmathsetmacro\PhiTwo{180+(\az-90)-\angle}
% % coordinates for transformed surface lines
\pgfmathsetmacro\sinPhiOne{{sin(\PhiOne)}}
\pgfmathsetmacro\cosPhiOne{{cos(\PhiOne)}}
\pgfmathsetmacro\sinPhiTwo{{sin(\PhiTwo)}}
\pgfmathsetmacro\cosPhiTwo{{cos(\PhiTwo)}}
% % angles for original surface lines
\pgfmathsetmacro\sinazp{{sin(\az-90)}}
\pgfmathsetmacro\cosazp{{cos(\az-90)}}
\pgfmathsetmacro\sinazm{{sin(90-\az)}}
\pgfmathsetmacro\cosazm{{cos(90-\az)}}
% % draw basis circle
\tdplotdrawarc[tdplot_main_coords,thick]{(O)}{\R}{\PhiOne}{360+\PhiTwo}{anchor=north}{}
\tdplotdrawarc[tdplot_main_coords,dashed]{(O)}{\R}{\PhiTwo}{\PhiOne}{anchor=north}{}
% % displaying tranformed surface of the cone (rotated)
\draw[thick] (0,0,\v) -- (\R*\cosPhiOne,\R*\sinPhiOne,0);
\draw[thick] (0,0,\v) -- (\R*\cosPhiTwo,\R*\sinPhiTwo,0);
\end{tikzpicture}
\end{document}
```
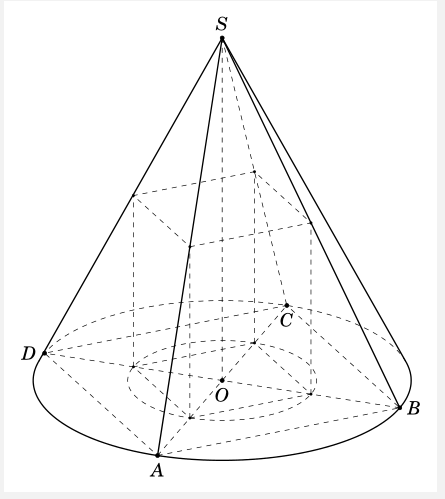
How to draw this picture by another way?