How to draw rectangular parallelepiped inside a pyramid? - TeX

TopAnswers TeX

Top Answer

user 3.14159

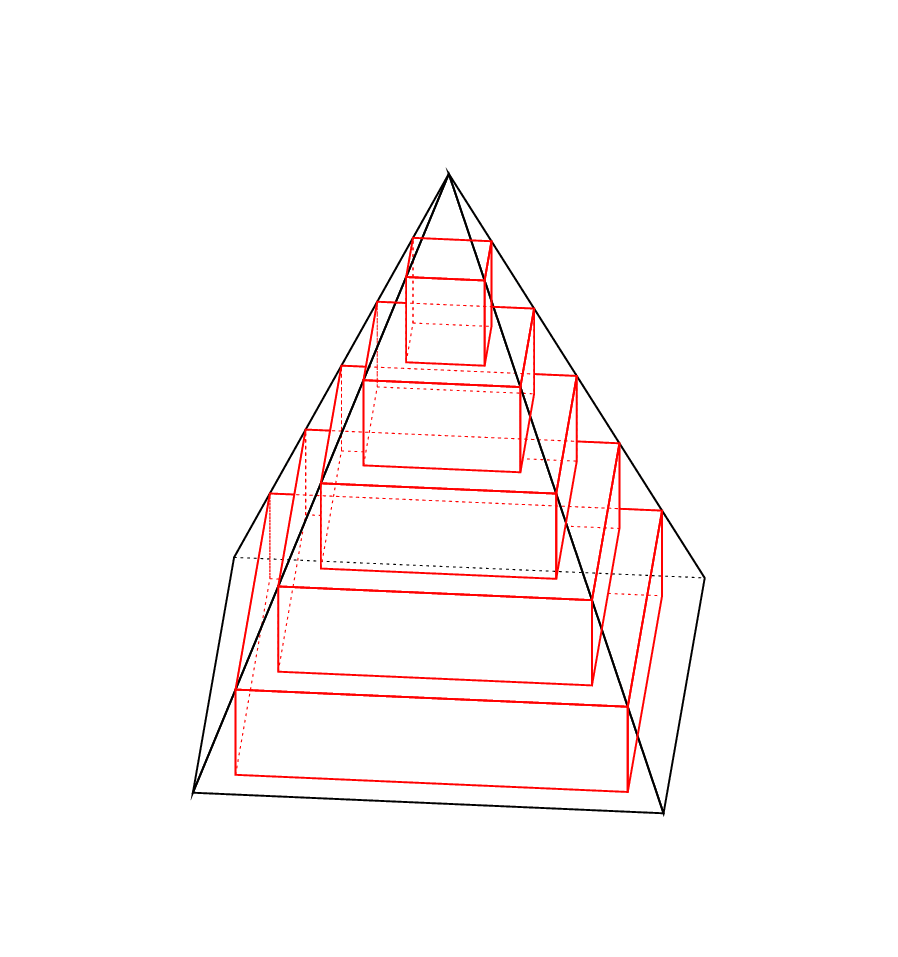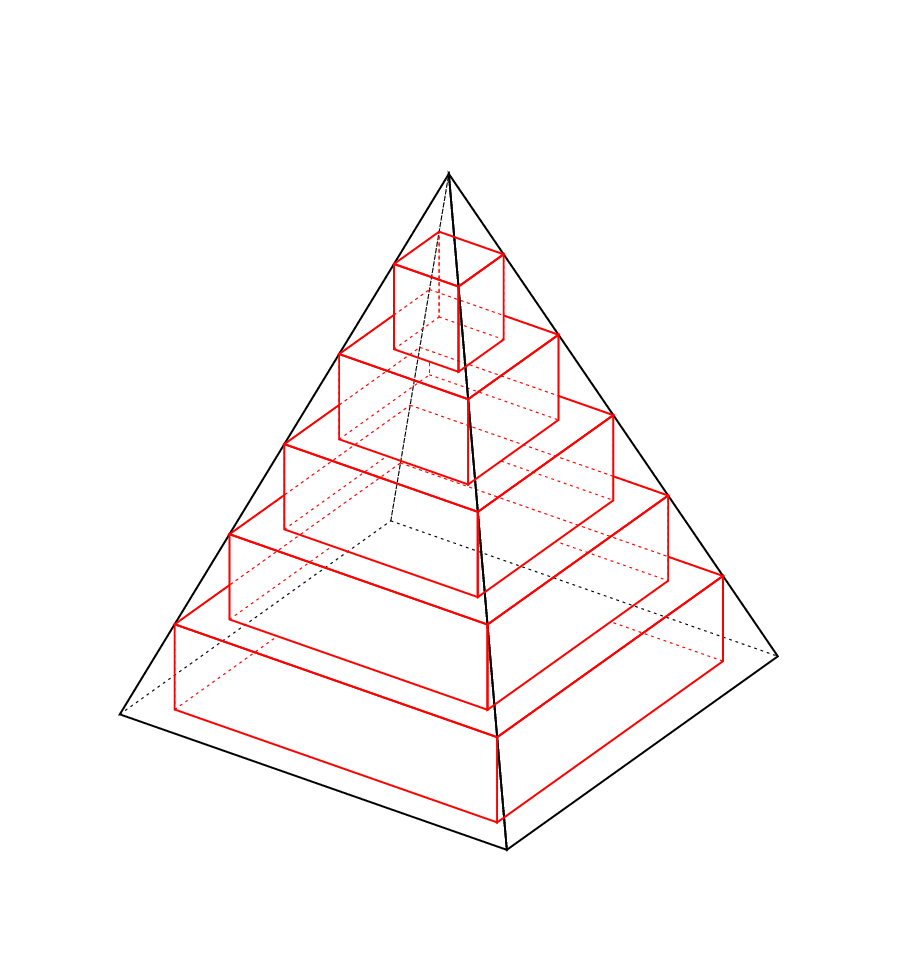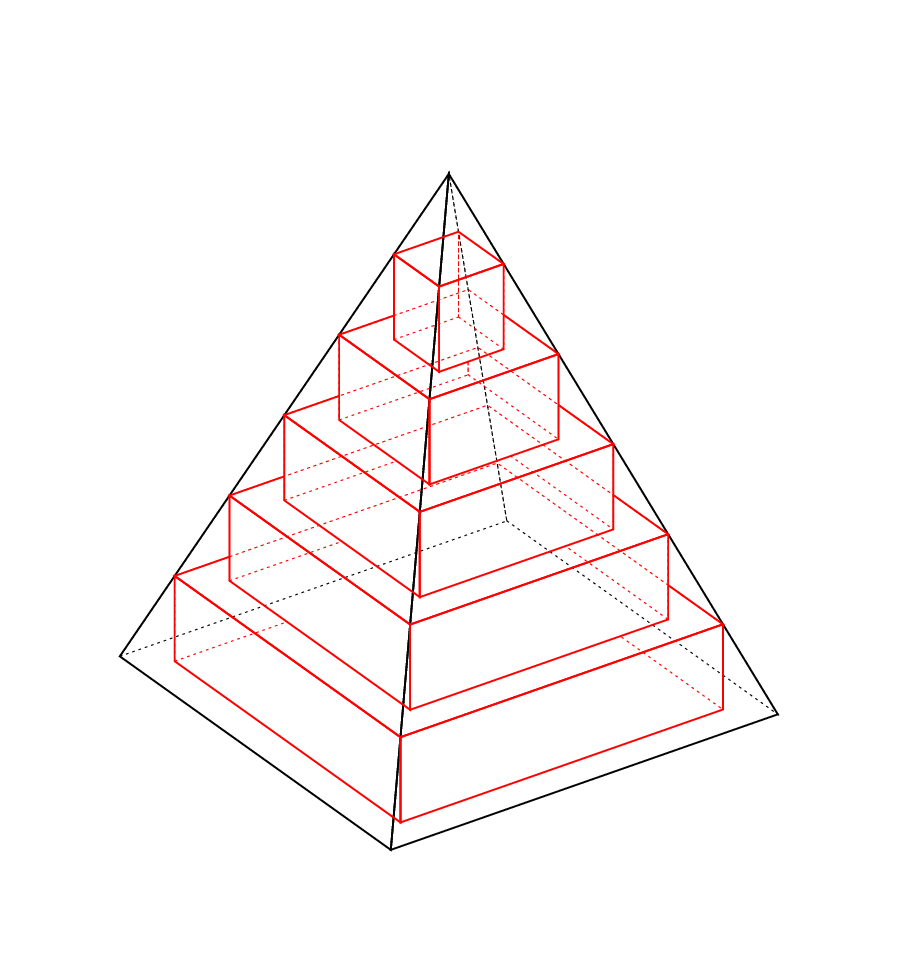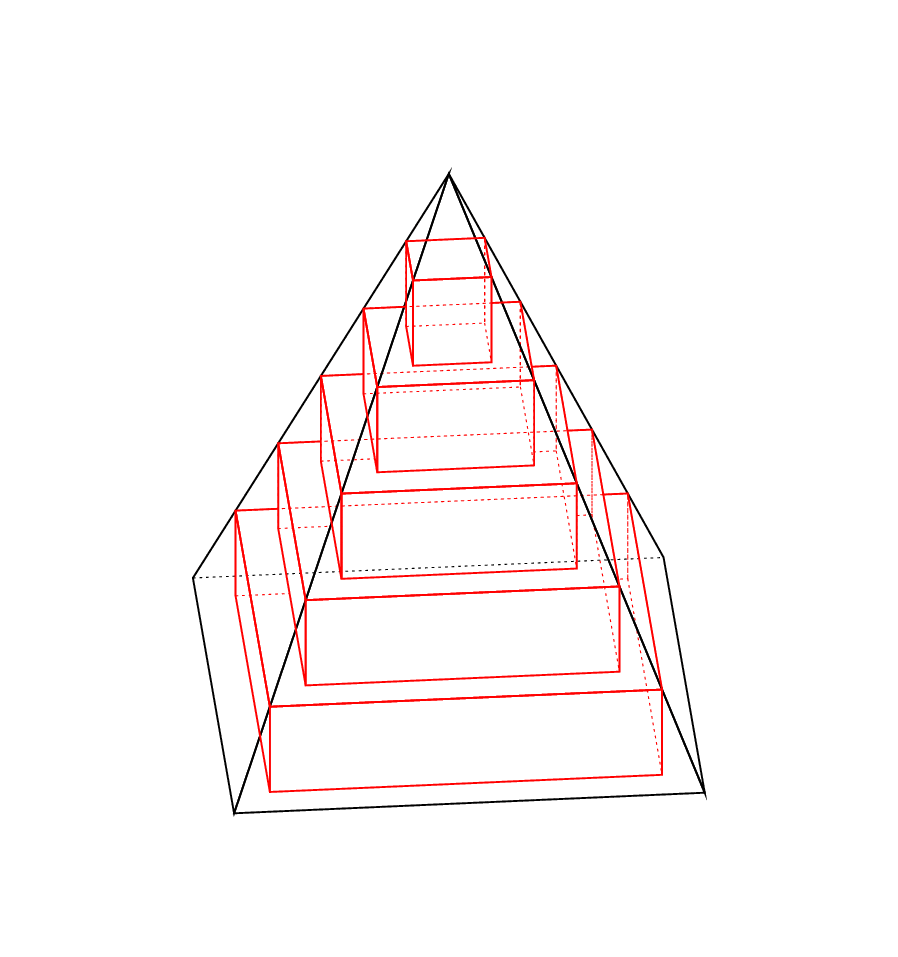
Ususally it is rather hard to check whether a line gets blocked by another object. In this case one can make things work with some reversed clips. This should give you the correct picture as long as you do not change the view angle `theta` too much.

```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
% https://tex.stackexchange.com/a/59168
\tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) rectangle (12383.99999pt,12383.99999pt)}}}
\begin{document}
\begin{tikzpicture}[declare function={a=2;h=5;}]
 \begin{scope}[3d/install view={phi=70,psi=0,theta=70}]
  \path (-a,-a,0) coordinate (A) (-a,a,0) coordinate (B)
   (a,a,0) coordinate (C) (a,-a,0) coordinate (D)
   (0,0,h) coordinate (T) (0,0,h/2) coordinate (I);
  \tikzset{3d/polyhedron/.cd,O={(I)},fore/.style={fill=none},
  	draw face with corners={{(A)},{(B)},{(T)}},
	draw face with corners={{(B)},{(C)},{(T)}},
	draw face with corners={{(C)},{(D)},{(T)}},
	draw face with corners={{(D)},{(A)},{(T)}}} 
  \edef\Xmax{6}	
  \begin{scope}[3d/polyhedron/.cd,O={(I)},
   	fore/.style={fill=none,draw=red},back/.style={fill=none,draw=red,densely dashed}] 
   \foreach \X [count=\Y] in
   {\the\numexpr\Xmax-1,\the\numexpr\Xmax-2,...,1}	
   {\pgfmathsetmacro{\myx}{(\Xmax-(\X))*a/\Xmax}
	\pgfmathsetmacro{\myy}{h*(\X)/\Xmax}
	\pgfmathsetmacro{\myz}{h*(\X-1)/\Xmax}
	\path (-\myx,-\myx,\myz) coordinate (A0-\Y) (-\myx,\myx,\myz) coordinate (B0-\Y)
     (\myx,\myx,\myz) coordinate (C0-\Y) (\myx,-\myx,\myz) coordinate (D0-\Y)
	 (-\myx,-\myx,\myy) coordinate (A1-\Y) (-\myx,\myx,\myy) coordinate (B1-\Y)
     (\myx,\myx,\myy) coordinate (C1-\Y) (\myx,-\myx,\myy) coordinate (D1-\Y);
	\tikzset{3d/polyhedron/.cd,
  	 draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}},
	 draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}},
	 draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}},
	 draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}}}  
	\ifnum\Y=1
	 \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	\else
     \pgfmathtruncatemacro{\Z}{\Y-1}
	 \begin{scope}
	  \clip (A0-\Z) -- (B0-\Z) -- (B1-\Z) -- (A1-\Z) -- cycle [reverseclip];
	  \clip (B0-\Z) -- (C0-\Z) -- (C1-\Z) -- (C1-\Z) -- cycle [reverseclip];
	  \clip (C0-\Z) -- (D0-\Z) -- (D1-\Z) -- (C1-\Z) -- cycle [reverseclip];
	  \clip (D0-\Z) -- (A0-\Z) -- (A1-\Z) -- (D1-\Z) -- cycle [reverseclip];
	  \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	 \end{scope}
	\fi	  
   }
  \end{scope}
 \end{scope}
\end{tikzpicture}
\end{document}
```
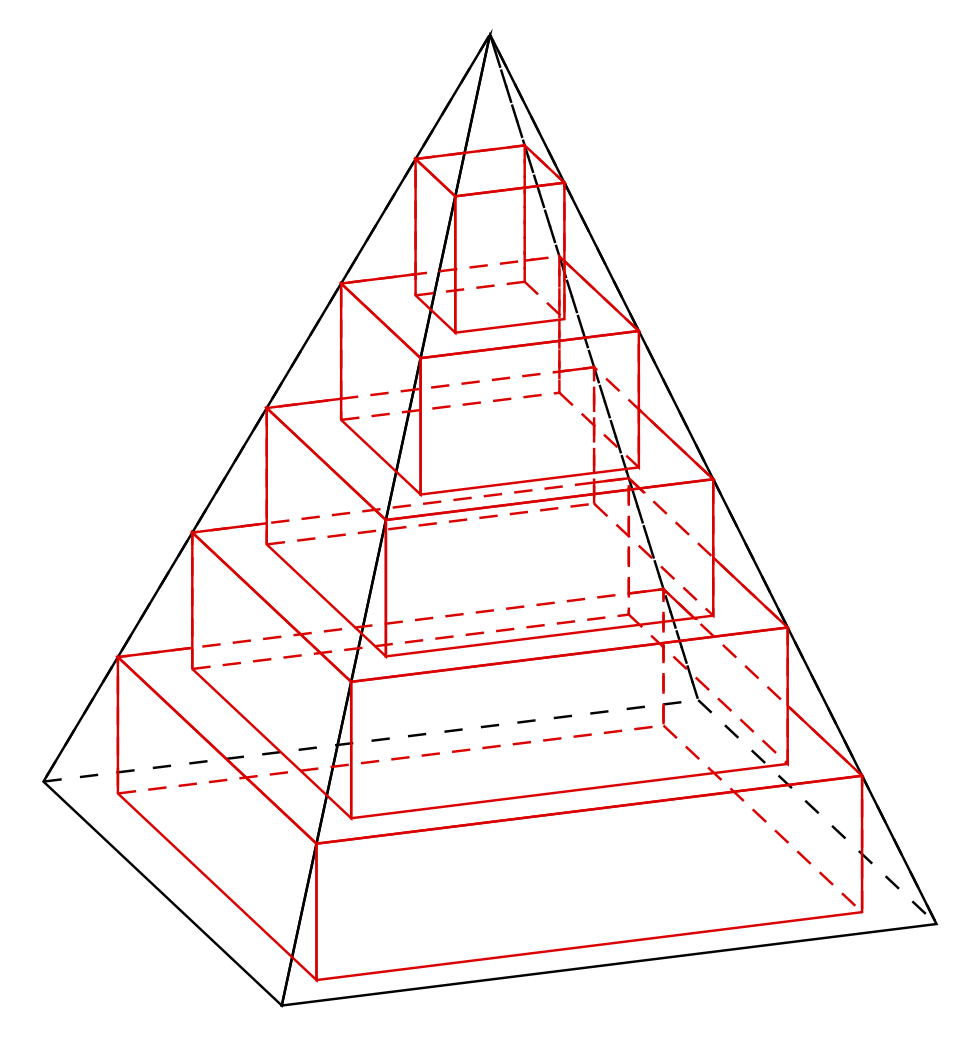
![Screen Shot 2020-10-17 at 9.40.01 AM.png](/image?hash=8d899a84076891faf5b2eb4dd022ebc9fdef28a08c1c8dbab59cb87862c44286)

The reverse clip method has glitches when one combines too many reverse clips and/or some contours have the "wrong" orientation. For this reason I added a style for the convex hull of points. After I was done, I realized that [solutions exist already](https://tex.stackexchange.com/questions/249860/compute-and-draw-a-convex-hull). I did not understand all strategies there but believe that I basically rediscovered [this strategy](https://tex.stackexchange.com/a/250354). At a given point I may add the style to the `3dtools` library because it may allow us to tackle many more cases than previously thought: just collect all faces that are drawn already and are in the foreground and use some clips and reverse clips to draw the solid or dashed lines further back. Of course one will still need reliable and simple methods to decide wheter a face is further back.

```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
% https://tex.stackexchange.com/a/59168
\tikzset{reverseclip/.style={overlay,insert
path={(-12383.99999pt,-12383.99999pt) -| (12383.99999pt,12383.99999pt) -| cycle}}}
\makeatletter
\pgfmathdeclarefunction{x2d}{1}{%
\begingroup%
\pgf@process{\pgfpointanchor{#1}{center}}%
\pgfmathparse{\pgf@x}%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%
\pgfmathdeclarefunction{y2d}{1}{%
\begingroup%
\pgf@process{\pgfpointanchor{#1}{center}}%
\pgfmathparse{\pgf@y}%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%

\tikzset{convex hull of/.code={% expects a list of points
\edef\pgfutil@tmpl{#1}% store the list for manipulations
\edef\pgfutil@tmpp{}% path to be constructed
\c@pgf@counta1%
\pgfutil@for\pgfutil@tmpa:={\pgfutil@tmpl}\do{%
\ifnum\c@pgf@counta=1\relax
\pgfmathsetmacro{\pgfutil@tmpb}{x2d("\pgfutil@tmpa")}% min
\edef\pgfutil@tmpd{\pgfutil@tmpa}% leftmost point
\else
\pgfmathsetmacro{\pgfutil@tmpc}{x2d("\pgfutil@tmpa")}% x coordinate
\ifdim\pgfutil@tmpc pt<\pgfutil@tmpb pt\relax
\edef\pgfutil@tmpb{\pgfutil@tmpc}% new min
\edef\pgfutil@tmpd{\pgfutil@tmpa}% new leftmost point
\fi
\fi
\advance\c@pgf@counta by1%
}
\edef\pgfutil@tmpp{(\pgfutil@tmpd)}%
\edef\pgfutil@tmpj{\pgfutil@tmpd}%
\edef\pgfutil@tmpe{90}% slope correction
\edef\pgfutil@tmpk{1}% first round flag
\loop
%\typeout{Removing  \pgfutil@tmpd}%
\edef\pgfutil@tmph{\noexpand\@removeelement{\pgfutil@tmpd}{\pgfutil@tmpl}{\noexpand\pgfutil@tmpl}}%
\pgfutil@tmph
%\typeout{List is now \pgfutil@tmpl}%
\c@pgf@countb1%
\pgfutil@for\pgfutil@tmpa:={\pgfutil@tmpl}\do{%
\pgfmathsetmacro{\pgfutil@tmpf}{Mod(atan2(y2d("\pgfutil@tmpa")-y2d("\pgfutil@tmpd"),
x2d("\pgfutil@tmpa")-x2d("\pgfutil@tmpd"))+\pgfutil@tmpe,360)}%
%\typeout{\the\c@pgf@countb: \pgfutil@tmpa\space has angle \pgfutil@tmpf.}%
\ifnum\c@pgf@countb=1\relax
\edef\pgfutil@tmpg{\pgfutil@tmpf}%
\edef\pgfutil@tmpi{\pgfutil@tmpa}%
\else
%\unless\ifdim\pgfutil@tmpf pt>180pt\relax
\ifdim\pgfutil@tmpf pt>\pgfutil@tmpg pt\relax
\edef\pgfutil@tmpg{\pgfutil@tmpf}%
\edef\pgfutil@tmpi{\pgfutil@tmpa}%
\fi
%\fi
\fi
\advance\c@pgf@countb by1%
}
%
\ifx\pgfutil@tmpi\pgfutil@tmpj\relax
\c@pgf@counta=2\relax
\else
\edef\pgfutil@tmpd{\pgfutil@tmpi}%
\edef\pgfutil@tmpp{\pgfutil@tmpp--(\pgfutil@tmpd)}%
\pgfmathsetmacro{\pgfutil@tmpe}{180+\pgfutil@tmpe-\pgfutil@tmpf}%
%\typeout{offset angle=\pgfutil@tmpe}%
\advance\c@pgf@counta by-1%
\fi
\ifnum\pgfutil@tmpk=1\relax
\edef\pgfutil@tmpl{\pgfutil@tmpl,\pgfutil@tmpj}% add the first point again
\edef\pgfutil@tmpk{0}%
\fi
\ifnum\c@pgf@counta>2\relax
\repeat
\edef\pgfutil@tmpp{\pgfutil@tmpp--cycle}%
\tikzset{insert path=\pgfutil@tmpp}%
}
}
\makeatother
\begin{document}
\begin{tikzpicture}[declare function={a=2;h=5;},
	3d/polyhedron/.cd,fore/.style={fill=none,draw,solid},
	back/.style={fill=none,draw,densely dashed}]
 \begin{scope}[3d/install view={phi=70,psi=0,theta=70},
 	3d/polyhedron/.cd,O={(I)},]
  \path (-a,-a,0) coordinate (A) (-a,a,0) coordinate (B)
   (a,a,0) coordinate (C) (a,-a,0) coordinate (D)
   (0,0,h) coordinate (T) (0,0,h/2) coordinate (I);
  \tikzset{3d/polyhedron/.cd,O={(I)},
  	draw face with corners={{(A)},{(B)},{(T)}},
	draw face with corners={{(B)},{(C)},{(T)}},
	draw face with corners={{(C)},{(D)},{(T)}},
	draw face with corners={{(D)},{(A)},{(T)}}} 
  \edef\Xmax{6}	
  \begin{scope}[3d/polyhedron/.cd,O={(I)},
   	fore/.append style={draw=red},
	back/.append style={draw=none}] 
   \foreach \X [count=\Y] in
   {\the\numexpr\Xmax-1,\the\numexpr\Xmax-2,...,1}	
   {\pgfmathsetmacro{\myx}{(\Xmax-(\X))*a/\Xmax}
	\pgfmathsetmacro{\myy}{h*(\X)/\Xmax}
	\pgfmathsetmacro{\myz}{h*(\X-1)/\Xmax}
	\path (-\myx,-\myx,\myz) coordinate (A0-\Y) (-\myx,\myx,\myz) coordinate (B0-\Y)
     (\myx,\myx,\myz) coordinate (C0-\Y) (\myx,-\myx,\myz) coordinate (D0-\Y)
	 (-\myx,-\myx,\myy) coordinate (A1-\Y) (-\myx,\myx,\myy) coordinate (B1-\Y)
     (\myx,\myx,\myy) coordinate (C1-\Y) (\myx,-\myx,\myy) coordinate (D1-\Y);
	\tikzset{3d/polyhedron/.cd,
  	 draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}},
	 draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}},
	 draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}},
	 draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}}}  
	\ifnum\Y=1
	 \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	\else
     \pgfmathtruncatemacro{\Z}{\Y-1}
	 \begin{scope}
	  \clip[convex hull of={A0-\Z,B0-\Z,C0-\Z,D0-\Z,A1-\Z,B1-\Z,C1-\Z,D1-\Z}] 
	  	[reverseclip];
	  \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	 \end{scope}
	\fi	  
   }
  \end{scope}
 \end{scope}
\end{tikzpicture}
\end{document}
```
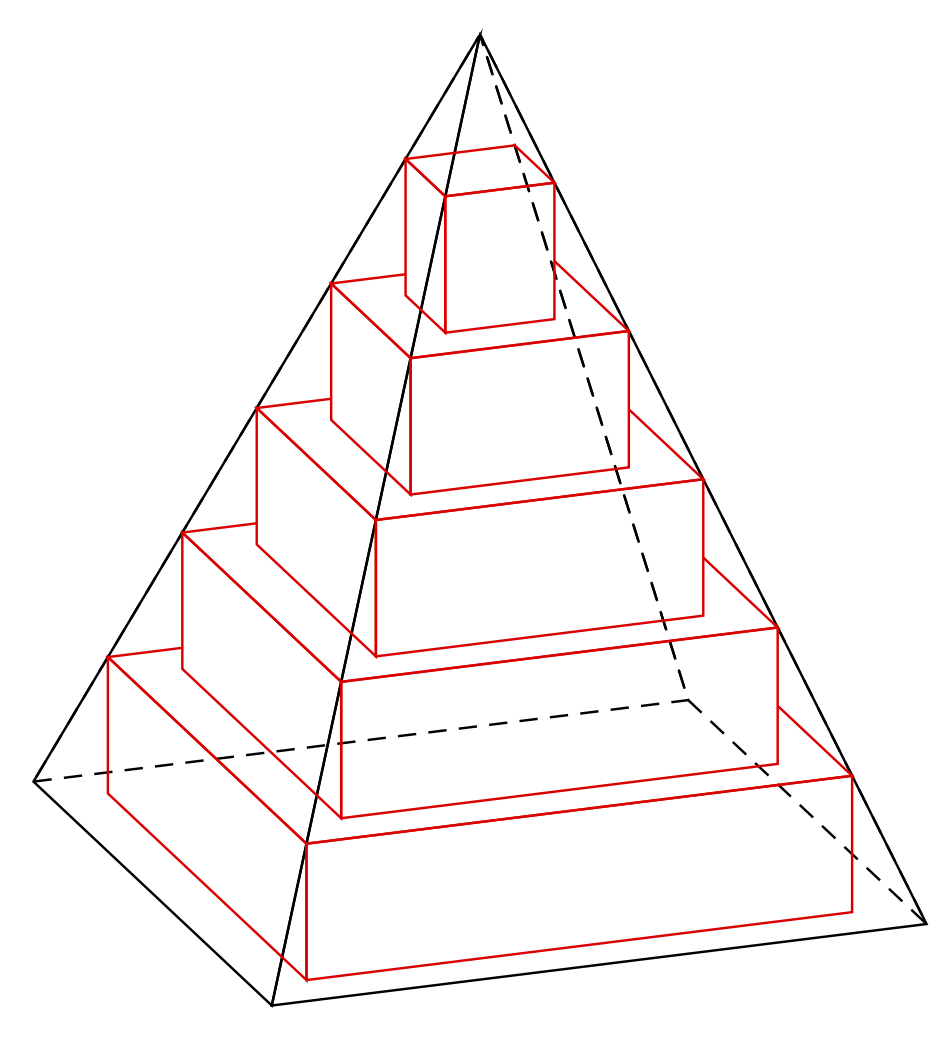
![Screen Shot 2020-10-17 at 10.16.44 AM.png](/image?hash=0247bbf4e505bb53231c27357865bc1631bf53cbd70f13e40cd351744c0636f9)

I added the `convex hull of` style to the [`3dtools` library](https://github.com/marmotghost/tikz-3dtools). The code can be shortened accordingly. 
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
% https://tex.stackexchange.com/a/59168
\tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) rectangle (12383.99999pt,12383.99999pt)}}}
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfdeclarelayer{behind}  
\pgfsetlayers{behind,background,main,foreground}
\begin{document}
\begin{tikzpicture}[declare function={a=2;h=5;},line cap=round,
	line join=round,
	3d/polyhedron/.cd,fore/.style={fill=none,draw,solid},
	back/.style={fill=none,draw,dash pattern=on 0.6pt off 1pt,very thin}]
 \begin{scope}[3d/install view={phi=70,psi=0,theta=70},
 	3d/polyhedron/.cd,O={(I)},]
  \path (-a,-a,0) coordinate (A) (-a,a,0) coordinate (B)
   (a,a,0) coordinate (C) (a,-a,0) coordinate (D)
   (0,0,h) coordinate (T) (0,0,h/2) coordinate (I);
  \tikzset{3d/polyhedron/.cd,O={(I)},fore layer=foreground,
  	back layer=behind,
  	draw face with corners={{(A)},{(B)},{(T)}},
	draw face with corners={{(B)},{(C)},{(T)}},
	draw face with corners={{(C)},{(D)},{(T)}},
	draw face with corners={{(D)},{(A)},{(T)}}} 
  \edef\Xmax{6}	
  \begin{scope}[3d/polyhedron/.cd,O={(I)},
   	fore/.append style={draw=red},
	back/.append style={draw=red}] 
   \foreach \X [count=\Y] in
   {\the\numexpr\Xmax-1,\the\numexpr\Xmax-2,...,1}	
   {\pgfmathsetmacro{\myx}{(\Xmax-(\X))*a/\Xmax}
	\pgfmathsetmacro{\myy}{h*(\X)/\Xmax}
	\pgfmathsetmacro{\myz}{h*(\X-1)/\Xmax}
	\path (-\myx,-\myx,\myz) coordinate (A0-\Y) (-\myx,\myx,\myz) coordinate (B0-\Y)
     (\myx,\myx,\myz) coordinate (C0-\Y) (\myx,-\myx,\myz) coordinate (D0-\Y)
	 (-\myx,-\myx,\myy) coordinate (A1-\Y) (-\myx,\myx,\myy) coordinate (B1-\Y)
     (\myx,\myx,\myy) coordinate (C1-\Y) (\myx,-\myx,\myy) coordinate (D1-\Y);
	\tikzset{3d/polyhedron/.cd,
  	 draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}},
	 draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}},
	 draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}},
	 draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}}}  
	\ifnum\Y=1
	 \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	\else
     \pgfmathtruncatemacro{\Z}{\Y-1}
	 \begin{scope}
	  \clip (A0-\Z) -- (D0-\Z) -- (C0-\Z) -- (C1-\Z) -- (B1-\Z)
	   -- (A1-\Z) -- cycle [reverseclip];
	  \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	 \end{scope}
	\fi	  
   }
  \end{scope}
 \end{scope}
\end{tikzpicture}
\end{document}
```
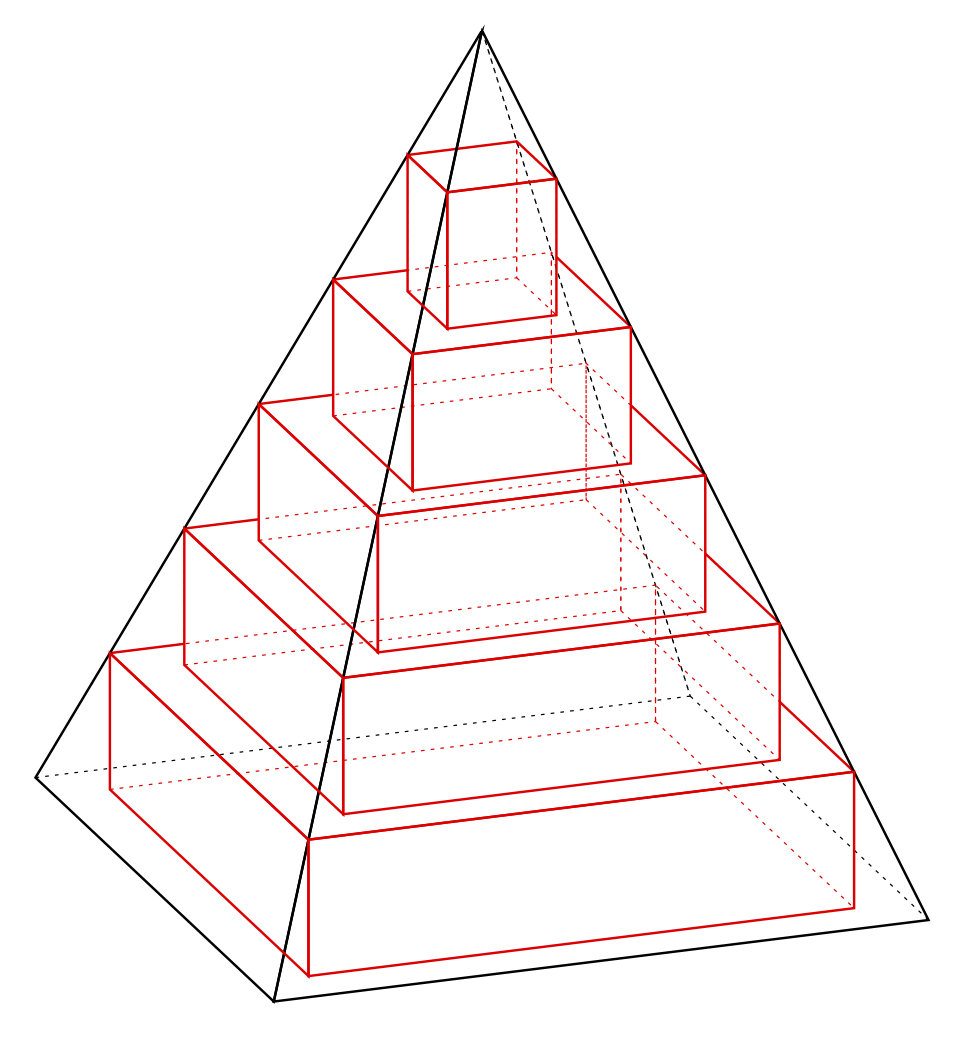
![Screen Shot 2020-10-17 at 10.49.59 PM.png](/image?hash=47cba1f6c4250a0ebd7e2348da5561b717cd6a7e9884bb263f925a609f21dd96)

Here is an animated version based on [this comment](https://topanswers.xyz/transcript?room=1472&id=77818#c77818).
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
% https://tex.stackexchange.com/a/59168
% Notice the change of orientation here, i.e. no rectangle
\tikzset{reverseclip/.style={overlay,insert
path={(-12383.99999pt,-12383.99999pt) -| (12383.99999pt,12383.99999pt) -| cycle}}}
\pgfdeclarelayer{background} 
\pgfdeclarelayer{foreground}
\pgfdeclarelayer{behind}  
\pgfsetlayers{behind,background,main,foreground}
\begin{document}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{60}{\Angle}
\begin{tikzpicture}[declare function={a=2;h=5;},line cap=round,
	line join=round,tdplot_main_coords,
	3d/polyhedron/.cd,fore/.style={fill=none,draw,solid},
	back/.style={fill=none,draw,dash pattern=on 0.6pt off 1pt,very thin}]
 \path[tdplot_screen_coords,use as bounding box] (-3.5,-2) rectangle (3.5,5.5);
 \begin{scope}[3d/polyhedron/.cd,O={(I)},]
  \path (-a,-a,0) coordinate (A) (-a,a,0) coordinate (B)
   (a,a,0) coordinate (C) (a,-a,0) coordinate (D)
   (0,0,h) coordinate (T) (0,0,h/2) coordinate (I);
  \tikzset{3d/polyhedron/.cd,O={(I)},fore layer=foreground,
  	back layer=behind,
  	draw face with corners={{(A)},{(B)},{(T)}},
	draw face with corners={{(B)},{(C)},{(T)}},
	draw face with corners={{(C)},{(D)},{(T)}},
	draw face with corners={{(D)},{(A)},{(T)}}} 
  \edef\Xmax{6}	
  \begin{scope}[3d/polyhedron/.cd,O={(I)},
   	fore/.append style={draw=red},
	back/.append style={draw=red}] 
   \foreach \X [count=\Y] in
   {\the\numexpr\Xmax-1,\the\numexpr\Xmax-2,...,1}	
   {\pgfmathsetmacro{\myx}{(\Xmax-(\X))*a/\Xmax}
	\pgfmathsetmacro{\myy}{h*(\X)/\Xmax}
	\pgfmathsetmacro{\myz}{h*(\X-1)/\Xmax}
	\path (-\myx,-\myx,\myz) coordinate (A0-\Y) (-\myx,\myx,\myz) coordinate (B0-\Y)
     (\myx,\myx,\myz) coordinate (C0-\Y) (\myx,-\myx,\myz) coordinate (D0-\Y)
	 (-\myx,-\myx,\myy) coordinate (A1-\Y) (-\myx,\myx,\myy) coordinate (B1-\Y)
     (\myx,\myx,\myy) coordinate (C1-\Y) (\myx,-\myx,\myy) coordinate (D1-\Y)
	 (0,0,0.5*\myy+0.5*\myz) coordinate (I-\Y);
	\ifnum\Y=1
	  \tikzset{3d/polyhedron/.cd,
	   draw face with corners={{(A1-\Y)},{(B1-\Y)},{(C1-\Y)},{(D1-\Y)}},
  	   draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}},
	   draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}},
	   draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}},
	   draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}}}  
	\else
     \pgfmathtruncatemacro{\Z}{\Y-1}
	 %\begin{scope}
	  \draw[red,dash pattern=on 0.6pt off 1pt,very thin] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle;
	  \tikzset{3d/polyhedron/.cd,O={(I-\Y)},
	   before hidden/.code={
	   \clip[convex hull of={A0-\Z,B0-\Z,C0-\Z,D0-\Z,A1-\Z,B1-\Z,C1-\Z,D1-\Z}] 
	  	[reverseclip];},
	   before visible/.code={\clip[convex hull of={A0-\Z,B0-\Z,C0-\Z,D0-\Z,A1-\Z,B1-\Z,C1-\Z,D1-\Z}] 
	  	[reverseclip];},
  	   draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}},
	   draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}},
	   draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}},
	   draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}},
	   draw face with corners={{(A1-\Y)},{(B1-\Y)},{(C1-\Y)},{(D1-\Y)}}}  
	 %\end{scope}
	\fi	  
   }
  \end{scope}
 \end{scope}
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=134aa19f5a8ae89c158e1ea593363cc6ee7e425eb182c4cef378fa456ebd5b64)

This yields a random coordinate in a triangle. However, the distribution may not be flat, i.e. not every point may be obtained with the same probability. ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{3dtools} \begin{document} \begin{tikzpicture}[3d/install view={theta=60,phi=110}] \path (0,0,0) coordinate (O) (2,3,0) coordinate (A) (-2,-5,0) coordinate (B) [/utils/exec=\pgfmathsetmacro{\myrndA}{rnd} \pgfmathsetmacro{\myrndB}{rnd*(1-\myrndA)}, 3d coordinate={(A-O)=(A)-(O)},% <- unnecessary if O is at origin 3d coordinate={(B-O)=(B)-(O)},% <- unnecessary if O is at origin 3d coordinate={(R_1)=\myrndA*(A-O)+\myrndB*(B-O)}]; \draw (O) -- (A) -- (B) -- cycle foreach \X in {O,A,B,R_1} {(\X) node[circle,inner sep=1pt,fill,label=below:$\X$]{}}; \end{tikzpicture} \end{document} ```

My code ```\documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{3dtools} \begin{document} \begin{tikzpicture}[3d/install view={theta=70,phi=110}] \path (0,0,0) coordinate (O) (1,3,5) coordinate (A) [/utils/exec=\pgfmathsetmacro{\myrnd}{rnd}, 3d coordinate={(R_1)=\myrnd*(A)}]; \path (2,-1,2) coordinate (B) [/utils/exec=\pgfmathsetmacro{\myrnd}{rnd}, 3d coordinate={(A-B)=(A)-(B)}, 3d coordinate={(R_2)=(B)+\myrnd*(A-B)}]; \draw (O) -- (A) (B) -- (A) foreach \X in {O,A,B,R_1,R_2} {(\X) node[circle,inner sep=1pt,fill,label=below:$\X$]{}}; \end{tikzpicture} \begin{tikzpicture} \path { (rnd*360:rnd*3) coordinate (M) node[circle,inner sep=1pt,fill,label={below:M}]{}}; \draw[convex hull of={O,A,B,M}]; \end{tikzpicture} \end{document} ```

I am reading in your manual ```\begin{tikzpicture} \path foreach \X in {1,...,10} { (rnd*360:rnd*3) coordinate (p\X) node[circle,inner sep=1pt,fill,label={below:$p_{\X}$}]{}}; \draw[convex hull of={p1,p2,p3,p4,p5,p6,p7,p8,p9,p10}]; \end{tikzpicture} ```

``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{3dtools} \begin{document} \begin{tikzpicture}[3d/install view={theta=70,phi=110}] \path (0,0,0) coordinate (O) (1,3,5) coordinate (A) [/utils/exec=\pgfmathsetmacro{\myrnd}{rnd}, 3d coordinate={(R_1)=\myrnd*(A)}]; \path (2,-1,2) coordinate (B) [/utils/exec=\pgfmathsetmacro{\myrnd}{rnd}, 3d coordinate={(A-B)=(A)-(B)}, 3d coordinate={(R_2)=(B)+\myrnd*(A-B)}]; \draw (O) -- (A) (B) -- (A) foreach \X in {O,A,B,R_1,R_2} {(\X) node[circle,inner sep=1pt,fill,label=below:$\X$]{}}; \end{tikzpicture} \end{document} ```

I added some "complete" dashes to the library, which do not suffer from the above-mentioned problem. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{fouriernc} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} % https://tex.stackexchange.com/a/59168 % Notice the change of orientation here, i.e. no rectangle \tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) -| (12383.99999pt,12383.99999pt) -| cycle}}} \begin{document} \foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{70}{\Angle} \begin{tikzpicture}[scale=1, tdplot_main_coords, line cap=round,line join=round, visible/.style={draw,thick,solid}, hidden/.style={draw,very thin,cheating dash}, 3d/polyhedron/.cd,fore/.style={fill=none,visible}, back/.style={fill=none,hidden,3d/polyhedron/complete dashes}] \pgfmathsetmacro\a{6} \pgfmathsetmacro\R{{\a*sqrt(2)/2}} %radius of base \pgfmathsetmacro\v{\R} % hight of pyramid \pgfmathsetmacro\b{{2*\v*\R/(sqrt(2)*\v+2*\R)}} %side of cube \pgfmathsetmacro\c{\b*sqrt(2)/2} \path[tdplot_screen_coords,use as bounding box] (-1.1*\a,-0.6*\a) rectangle (1.1*\a,0.6*\a+\R); \path (0,0,0) coordinate (O) (\R,0,0) coordinate (A) (0,\R,0) coordinate (B) (-\R,0,0) coordinate (C) (0,-\R,0) coordinate (D) (\c,0,0) coordinate (M) (0,\c,0) coordinate (N) (-\c,0,0) coordinate (P) (0,-\c,0) coordinate (Q); \path (\c,0,\b) coordinate (M') (0,\c,\b) coordinate (N') (-\c,0,\b) coordinate (P') (0,-\c,\b) coordinate (Q'); \path (0,0,\v) coordinate (S) (0,0,\b) coordinate (S') (0,0,\b/2) coordinate (I); \tikzset{3d/polyhedron/.cd,O={(I)}, draw face with corners={{(M')},{(N')},{(P')},{(Q')}}, draw face with corners={{(M')},{(N')},{(N)},{(M)}}, draw face with corners={{(N')},{(P')},{(P)},{(N)}}, draw face with corners={{(P')},{(Q')},{(Q)},{(P)}}, draw face with corners={{(Q')},{(M')},{(M)},{(Q)}}, draw face with corners={{(M)},{(N)},{(P)},{(Q)}}, draw face with corners={{(A)},{(B)},{(S)}}, draw face with corners={{(B)},{(C)},{(S)}}, draw face with corners={{(C)},{(D)},{(S)}}, draw face with corners={{(D)},{(A)},{(S)}}} \foreach \v/\position in {O/below,A/below, B/right, C/right, D/left, S/above} {\draw[draw =black, fill=black] (\v) circle (1.5pt) node [\position=0.2mm] {$\v$}; } \begin{scope} \draw[hidden] (A) -- (C); \draw[hidden] (B) -- (D); \draw[hidden] (S') -- (O); \draw[visible] (S') -- (S) foreach \X in {M,N,P,Q} {(S) -- (\X')}; \clip[convex hull of={M,N,P,Q,M',N',P',Q'}] [reverseclip]; \draw[visible] (A) -- (C) (B) -- (D) (A) -- (B) -- (C) -- (D) -- cycle foreach \X in {A,B,C,D} {(S) -- (\X)}; \end{scope} \foreach \Y in {M, N, P, Q, M', N', P', Q'} {\fill (\Y) circle[radius=1.2pt];} \end{tikzpicture}} \end{document} ``` ![ani.gif](/image?hash=89e97729ef03ff614724163791fab5ac5d2d36ce15e25c416188496a630b6c56)

And this is a slightly different interpretation of "repair". ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{fouriernc} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} % https://tex.stackexchange.com/a/59168 % Notice the change of orientation here, i.e. no rectangle \tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) -| (12383.99999pt,12383.99999pt) -| cycle}}} \begin{document} \foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{70}{\Angle} \begin{tikzpicture}[scale=1, tdplot_main_coords, line cap=round,line join=round, visible/.style={draw,thick,solid}, hidden/.style={draw,dash pattern=on 0.6pt off 1pt,very thin}, 3d/polyhedron/.cd,fore/.style={fill=none,visible}, back/.style={fill=none,hidden}] \pgfmathsetmacro\a{6} \pgfmathsetmacro\R{{\a*sqrt(2)/2}} %radius of base \pgfmathsetmacro\v{\R} % hight of pyramid \pgfmathsetmacro\b{{2*\v*\R/(sqrt(2)*\v+2*\R)}} %side of cube \pgfmathsetmacro\c{\b*sqrt(2)/2} \path[tdplot_screen_coords,use as bounding box] (-1.1*\a,-0.6*\a) rectangle (1.1*\a,0.6*\a+\R); \path (0,0,0) coordinate (O) (\R,0,0) coordinate (A) (0,\R,0) coordinate (B) (-\R,0,0) coordinate (C) (0,-\R,0) coordinate (D) (\c,0,0) coordinate (M) (0,\c,0) coordinate (N) (-\c,0,0) coordinate (P) (0,-\c,0) coordinate (Q); \path (\c,0,\b) coordinate (M') (0,\c,\b) coordinate (N') (-\c,0,\b) coordinate (P') (0,-\c,\b) coordinate (Q'); \path (0,0,\v) coordinate (S) (0,0,\b) coordinate (S') (0,0,\b/2) coordinate (I); \tikzset{3d/polyhedron/.cd,O={(I)}, draw face with corners={{(M')},{(N')},{(P')},{(Q')}}, draw face with corners={{(M')},{(N')},{(N)},{(M)}}, draw face with corners={{(N')},{(P')},{(P)},{(N)}}, draw face with corners={{(P')},{(Q')},{(Q)},{(P)}}, draw face with corners={{(Q')},{(M')},{(M)},{(Q)}}, draw face with corners={{(M)},{(N)},{(P)},{(Q)}}, draw face with corners={{(A)},{(B)},{(S)}}, draw face with corners={{(B)},{(C)},{(S)}}, draw face with corners={{(C)},{(D)},{(S)}}, draw face with corners={{(D)},{(A)},{(S)}}} \foreach \v/\position in {O/below,A/below, B/right, C/right, D/left, S/above} {\draw[draw =black, fill=black] (\v) circle (1.5pt) node [\position=0.2mm] {$\v$}; } \begin{scope} \draw[hidden] (A) -- (C) (B) -- (D) (S') -- (O); \draw[visible] (S') -- (S) foreach \X in {M,N,P,Q} {(S) -- (\X')}; \clip[convex hull of={M,N,P,Q,M',N',P',Q'}] [reverseclip]; \draw[visible] (A) -- (C) (B) -- (D) (A) -- (B) -- (C) -- (D) -- cycle foreach \X in {A,B,C,D} {(S) -- (\X)}; \end{scope} \foreach \Y in {M, N, P, Q, M', N', P', Q'} {\fill (\Y) circle[radius=1.2pt];} \end{tikzpicture}} \end{document} ``` ![ani.gif](/image?hash=508b4e49dc03d65c375cb7c15c0045db2abf4854c1ddc9a84003c2181ae44f3c)

P.S. I plan to create a dash style that continues to look good if you draw multiple dashed lines on top of each other. The problem is that the dash phases of the individual lines do not match up, so if you draw several dashed lines with different phases on top of each other the line will eventually become solid. I am aware of the problem but did not have the time and passion to work on a solution.

I do not know what repair means, but maybe you want something like this. Note that I converted all coordinates to become something that can be used with `3dtools`. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{fouriernc} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} % https://tex.stackexchange.com/a/59168 % Notice the change of orientation here, i.e. no rectangle \tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) -| (12383.99999pt,12383.99999pt) -| cycle}}} \begin{document} \tdplotsetmaincoords{70}{110} \begin{tikzpicture}[scale=1, tdplot_main_coords, line cap=round,line join=round, visible/.style={draw,thick,solid}, hidden/.style={draw,dash pattern=on 0.6pt off 1pt,very thin}, 3d/polyhedron/.cd,fore/.style={fill=none,visible}, back/.style={fill=none,hidden}] \pgfmathsetmacro\a{6} \pgfmathsetmacro\R{{\a*sqrt(2)/2}} %radius of base \pgfmathsetmacro\v{\R} % hight of pyramid \pgfmathsetmacro\b{{2*\v*\R/(sqrt(2)*\v+2*\R)}} %side of cube \pgfmathsetmacro\c{\b*sqrt(2)/2} \path (0,0,0) coordinate (O) (\R,0,0) coordinate (A) (0,\R,0) coordinate (B) (-\R,0,0) coordinate (C) (0,-\R,0) coordinate (D) (\c,0,0) coordinate (M) (0,\c,0) coordinate (N) (-\c,0,0) coordinate (P) (0,-\c,0) coordinate (Q); \path (\c,0,\b) coordinate (M') (0,\c,\b) coordinate (N') (-\c,0,\b) coordinate (P') (0,-\c,\b) coordinate (Q'); \path (0,0,\v) coordinate (S) (0,0,\b) coordinate (S') (0,0,\b/2) coordinate (I); \tikzset{3d/polyhedron/.cd,O={(I)}, draw face with corners={{(M')},{(N')},{(P')},{(Q')}}, draw face with corners={{(M')},{(N')},{(N)},{(M)}}, draw face with corners={{(N')},{(P')},{(P)},{(N)}}, draw face with corners={{(P')},{(Q')},{(Q)},{(P)}}, draw face with corners={{(Q')},{(M')},{(M)},{(Q)}}, draw face with corners={{(M)},{(N)},{(P)},{(Q)}}, draw face with corners={{(A)},{(B)},{(S)}}, draw face with corners={{(B)},{(C)},{(S)}}, draw face with corners={{(C)},{(D)},{(S)}}, draw face with corners={{(D)},{(A)},{(S)}}} \foreach \v/\position in {O/below,A/below, B/right, C/right, D/left, S/above} {\draw[draw =black, fill=black] (\v) circle (1.5pt) node [\position=0.2mm] {$\v$}; } \begin{scope} \draw[hidden] (A) -- (C) (B) -- (D); \draw[visible] foreach \X in {M,N,P,Q} {(S) -- (\X')}; \clip[convex hull of={M,N,P,Q,M',N',P',Q'}] [reverseclip]; \draw[visible] (A) -- (C) (B) -- (D); \end{scope} \foreach \Y in {M, N, P, Q, M', N', P', Q'} {\fill (\Y) circle[radius=1.2pt];} \end{tikzpicture} \end{document} ``` ![Screen Shot 2020-10-19 at 9.32.27 AM.png](/image?hash=5c27aeb1771cdc109119d12cf24041622adb65dd8d742ca003953426943d11d0)

@marmot, re: [your answer](#a1671), How can I use this answer to rapair this code? ```\documentclass[border=1mm,12pt,tikz]{standalone} \usepackage{fouriernc} \usepackage{tikz-3dplot} \usetikzlibrary{calc,backgrounds} \begin{document} \tdplotsetmaincoords{70}{110} \pgfmathsetmacro\a{6} \pgfmathsetmacro\R{{\a*sqrt(2)/2}} %radius of base \pgfmathsetmacro\v{\R} % hight of pyramid \pgfmathsetmacro\b{{2*\v*\R/(sqrt(2)*\v+2*\R)}} %side of cube \pgfmathsetmacro\c{\b*sqrt(2)/2} \begin{tikzpicture} [scale=1, tdplot_main_coords, axis/.style={blue,thick}] \begin{scope}[canvas is xy plane at z=0] \path coordinate (O) at (0,0) coordinate (A) at (\R,0) coordinate (B) at (0,\R) coordinate (C) at (-\R,0) coordinate (D) at (0,-\R) coordinate (M) at (\c,0) coordinate (N) at (0,\c) coordinate (P) at (-\c,0) coordinate (Q) at (0,-\c); \end{scope} \begin{scope}[canvas is xy plane at z=\b] \path coordinate (M') at (\c,0) coordinate (N') at (0,\c) coordinate (P') at (-\c,0) coordinate (Q') at (0,-\c) ; \end{scope} \coordinate (S) at (0,0,\v); \foreach \v/\position in {O/below,A/below, B/right, C/right, D/left, S/above} {\draw[draw =black, fill=black] (\v) circle (1.5pt) node [\position=0.2mm] {$\v$}; } \foreach \X in {A,B,D} \draw[thick] (\X) -- (S) (D) -- (A) -- (B); \foreach \X in {M,N,P,Q} \draw[dashed] (\X) -- (\X'); \draw[dashed] (M) -- (N) -- (P) -- (Q) -- cycle (M') -- (N') -- (P') -- (Q') -- cycle (A) -- (C) (B) -- (D) (S)--(O) (S)-- (C) (D) -- (C) -- (B) ; \foreach \Y in {M, N, P, Q, M', N', P', Q'} \fill (\Y) circle[radius=1.2pt]; \end{tikzpicture} \end{document} ```

There are a few issues. First of all, no document class. Second, since you seem to want to work with `tikz-3dplot`, you also need to install the view with `tdplot_main_coords`. Then you did not use the convex hull, but a code that, as I said, does not work for rotated views. Please note also that for the convex hulls one needs to reverse the orientation for `reverse clip`. Finally, since we work with layers, we need to use the `before visible` and `before hidden` hooks. This is because otherwise clip does not work (which is why I installed the hooks in the first place). I post the repaired code at the end on my answer.

@marmot, re: [your answer](#a1671), I used '''\foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{60}{\Angle}``` Full code ```\documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools % https://tex.stackexchange.com/a/59168 \tikzset{reverseclip/.style={overlay,insert path={(-12383.99999pt,-12383.99999pt) rectangle (12383.99999pt,12383.99999pt)}}} \pgfdeclarelayer{background} \pgfdeclarelayer{foreground} \pgfdeclarelayer{behind} \pgfsetlayers{behind,background,main,foreground} \begin{document} \foreach \Angle in {5,15,...,355} {\tdplotsetmaincoords{60}{\Angle} \begin{tikzpicture}[declare function={a=2;h=5;},line cap=round, line join=round, 3d/polyhedron/.cd,fore/.style={fill=none,draw,solid}, back/.style={fill=none,draw,dash pattern=on 0.6pt off 1pt,very thin}] \begin{scope}[3d/polyhedron/.cd,O={(I)},] \path (-a,-a,0) coordinate (A) (-a,a,0) coordinate (B) (a,a,0) coordinate (C) (a,-a,0) coordinate (D) (0,0,h) coordinate (T) (0,0,h/2) coordinate (I); \tikzset{3d/polyhedron/.cd,O={(I)},fore layer=foreground, back layer=behind, draw face with corners={{(A)},{(B)},{(T)}}, draw face with corners={{(B)},{(C)},{(T)}}, draw face with corners={{(C)},{(D)},{(T)}}, draw face with corners={{(D)},{(A)},{(T)}}} \edef\Xmax{6} \begin{scope}[3d/polyhedron/.cd,O={(I)}, fore/.append style={draw=red}, back/.append style={draw=red}] \foreach \X [count=\Y] in {\the\numexpr\Xmax-1,\the\numexpr\Xmax-2,...,1} {\pgfmathsetmacro{\myx}{(\Xmax-(\X))*a/\Xmax} \pgfmathsetmacro{\myy}{h*(\X)/\Xmax} \pgfmathsetmacro{\myz}{h*(\X-1)/\Xmax} \path (-\myx,-\myx,\myz) coordinate (A0-\Y) (-\myx,\myx,\myz) coordinate (B0-\Y) (\myx,\myx,\myz) coordinate (C0-\Y) (\myx,-\myx,\myz) coordinate (D0-\Y) (-\myx,-\myx,\myy) coordinate (A1-\Y) (-\myx,\myx,\myy) coordinate (B1-\Y) (\myx,\myx,\myy) coordinate (C1-\Y) (\myx,-\myx,\myy) coordinate (D1-\Y); \tikzset{3d/polyhedron/.cd, draw face with corners={{(A0-\Y)},{(B0-\Y)},{(B1-\Y)},{(A1-\Y)}}, draw face with corners={{(B0-\Y)},{(C0-\Y)},{(C1-\Y)},{(B1-\Y)}}, draw face with corners={{(C0-\Y)},{(D0-\Y)},{(D1-\Y)},{(C1-\Y)}}, draw face with corners={{(D0-\Y)},{(A0-\Y)},{(A1-\Y)},{(D1-\Y)}}} \ifnum\Y=1 \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle; \else \pgfmathtruncatemacro{\Z}{\Y-1} \begin{scope} \clip (A0-\Z) -- (D0-\Z) -- (C0-\Z) -- (C1-\Z) -- (B1-\Z) -- (A1-\Z) -- cycle [reverseclip]; \draw[red] (A1-\Y) -- (B1-\Y) -- (C1-\Y) -- (D1-\Y) -- cycle; \end{scope} \fi } \end{scope} \end{scope} \end{tikzpicture}} \end{document}```

1 Answer