Three-dimensional spiral - TeX

TopAnswers TeX

Top Answer

user 3.14159

You can just draw a parametric curve. I added such a curve to your code.
```
\documentclass[tikz,margin=3mm]{standalone}
\usetikzlibrary{3d,arrows.meta,bending}
\usepackage{siunitx}
\begin{document}
\begin{tikzpicture}[x=(-45:1.2),z=(45:1.2),declare function={r=1;s=1/600;}]
  \draw (0,0,0) -- (4,0,0) node[right] {$x$}
    (0,0,0) -- (0,3,0) node[above] {$y$}
    (0,0,2) -- (0,0,-2) node[left] {$z$};
  \begin{scope}[canvas is xy plane at z=0]
    \draw[thick,red,->] (0,0) -- (80:2) node[above right] {$\mathbf{v}$};
    \draw (.4,0) arc (0:80:.4);
    \coordinate (x) at (30:.2);
  \end{scope}
  \draw (x) -- ++ (-.5,0) node[left] {\ang{85.0}};
  \draw[thick,green!50!black,->] (1,0,-1) -- (3,0,-1)
    node[midway,below left] {$\mathbf{B}$};
  \draw (1,0,2) -- (1,0,3) (2,0,2) -- (2,0,3);
  \draw[<->] (1,0,2.5) -- (2,0,2.5) node[midway,below left] {$p$};
  \foreach \X in {0,...,4}
  {\ifnum\X=4
    \draw[orange,thick,dashed] 
     plot[variable=\t,domain=180:270,smooth,samples=5]
     (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \else
    \draw[orange,thick,dashed] 
     plot[variable=\t,domain=180:360,smooth,samples=9]
     (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \fi
   \draw[orange,thick,-{Stealth[bend,length=3mm,width=1.5mm]}]
    plot[variable=\t,domain=0:90,smooth,samples=5]
	(s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \draw[orange,thick] plot[variable=\t,domain=0:180,smooth,samples=9]
  (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});}
\end{tikzpicture}
\end{document}
```
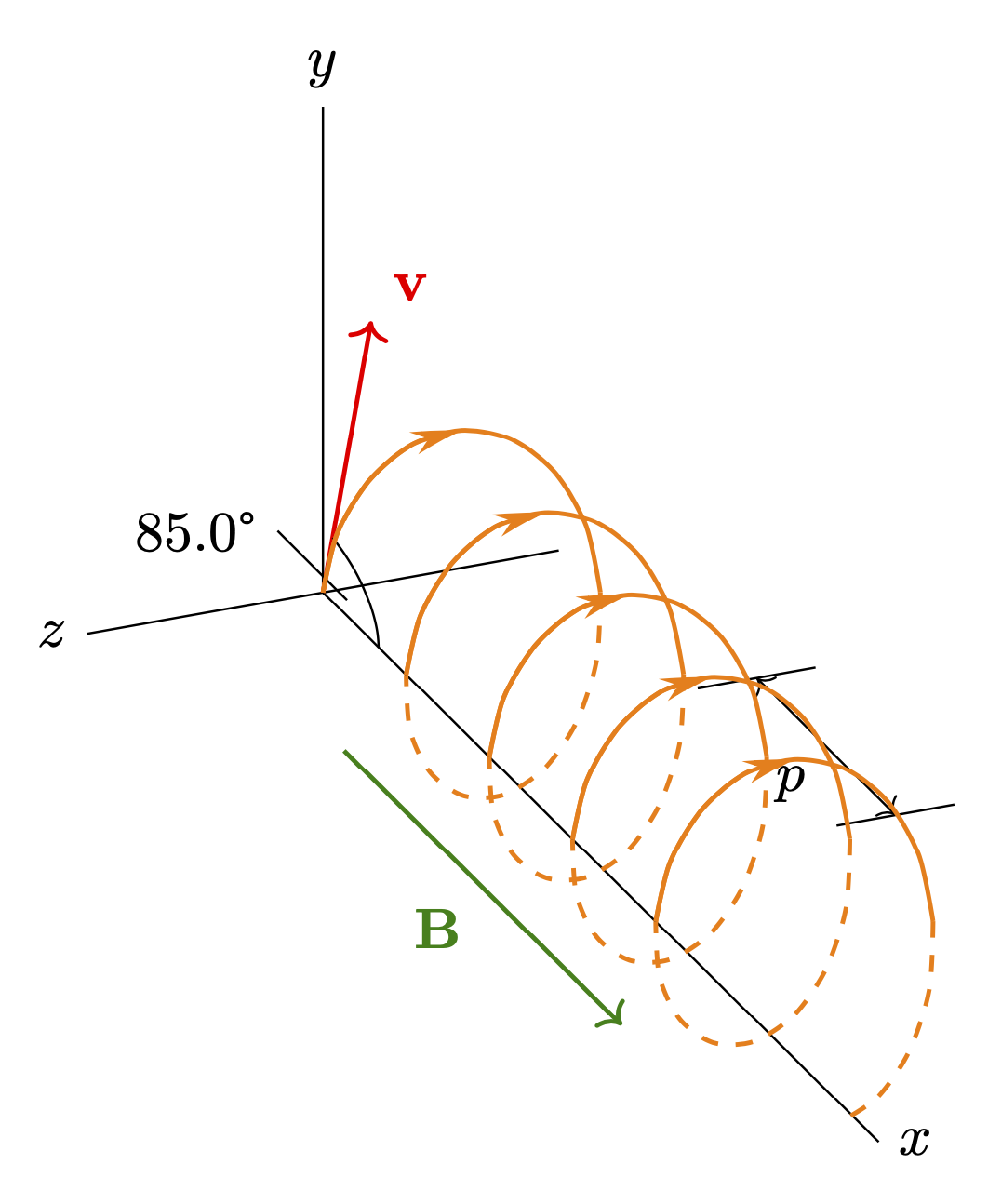
![Screen Shot 2020-10-14 at 8.43.44 AM.png](/image?hash=d669cc57df6778ea68ce68e12f9174280cadbe596050b93d1eaa27ad5fe932ba)

If you install an orthographic projection, you get something like
```
\documentclass[tikz,margin=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3d,arrows.meta,bending}
\usepackage{siunitx}
\begin{document}
\tdplotsetmaincoords{60}{70}
\begin{tikzpicture}[tdplot_main_coords,declare function={r=1;s=1/600;}]
 \path (0,0,1) coordinate (ey) (1,0,0) coordinate (ex) (0,1,0) coordinate (ez);
 \begin{scope}[x={(ex)},y={(ey)},z={(ez)}]
  \draw (0,0,0) -- (4,0,0) node[right] {$x$}
    (0,0,0) -- (0,3,0) node[above] {$y$}
    (0,0,2) -- (0,0,-2) node[left] {$z$};
  \begin{scope}[canvas is xy plane at z=0]
    \draw[thick,red,->] (0,0) -- (80:2) node[above right] {$\mathbf{v}$};
    \draw (.4,0) arc (0:80:.4);
    \coordinate (x) at (30:.2);
  \end{scope}
  \draw (x) -- ++ (-.5,0) node[left] {\ang{85.0}};
  \draw[thick,green!50!black,->] (1,0,-1) -- (3,0,-1)
    node[midway,below left] {$\mathbf{B}$};
  \draw (1,0,2) -- (1,0,3) (2,0,2) -- (2,0,3);
  \draw[<->] (1,0,2.5) -- (2,0,2.5) node[midway,below left] {$p$};
  \foreach \X in {0,...,4}
  {\ifnum\X=4
    \draw[orange,thick,dashed] 
     plot[variable=\t,domain=180:270,smooth,samples=5]
     (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \else
    \draw[orange,thick,dashed] 
     plot[variable=\t,domain=180:360,smooth,samples=9]
     (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \fi
   \draw[orange,thick,-{Stealth[bend,length=3mm,width=1.5mm]}]
    plot[variable=\t,domain=0:90,smooth,samples=5]
	(s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});
   \draw[orange,thick] plot[variable=\t,domain=0:180,smooth,samples=9]
  (s*\X*360+s*\t,{r*sin(\t)},{r-r*cos(\t)});}
 \end{scope}
\end{tikzpicture}
\end{document}
```
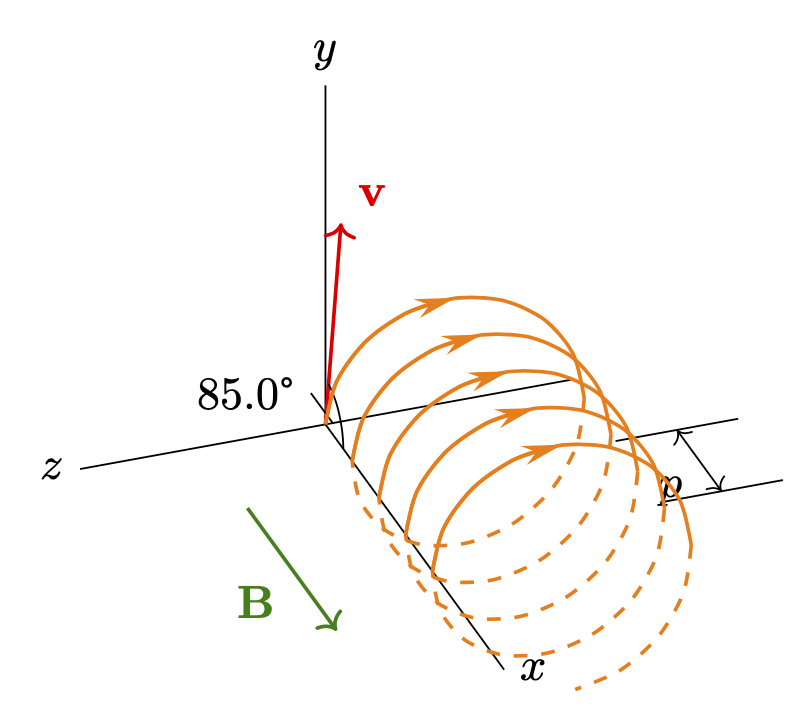
![Screen Shot 2020-10-14 at 9.01.12 AM.png](/image?hash=72e43e734aa1ba506c9da769653e445a9335636dc812bc1bd06466b9bbfba350)

You can adjust the parameters of `\tdplotsetmaincoords{60}{70}` to change the view. Note that your coordinate system has an unconventional orientation in that the orthogonal transformation that installs the view has determinant -1. In other words, in your picture the righthanded rather the lefthanded particles participate in the weak interactions. As illustrated [here](https://xkcd.com/2364/)

![Screen Shot 2020-10-14 at 9.04.56 AM.png](/image?hash=5ea13d3e3e30d69cc335cf0ccb462b90782d475f76e36b0b320b4ca47167c35b)

this may have unpleasant consequences. :smile_cat:

Well, I think this is what they believe to be true, and there are some reasons why that is. So it is an opinion, and rather than other opinions that people throw at each other on that site, there are even some arguments that support this opinion. At the same time, it is completely pointless in my opinion to make such comments, If you really want to go that route, you'd have to post at each PSTricks code that there is no reason to still use PSTricks. There are even more supporting arguments for this, but still users have the right to play with PSTricks. (Of course, when we are talking about the users who just translate an existing Ti*k*Z answer into PSTricks and post "their" code without attribution this is a bit different, but this also happens a lot.)

@marmot, re: [your answer](#a1660), another command of Black Mild from [here](https://tex.stackexchange.com/questions/575546/how-to-add-grid-and-define-z-domain-for-3d-plotting) ![ScreenHunter 1027.png](/image?hash=721ec7d284445ae3e66054757d54e383efbcad5100dc22cc219b5c3c75943aff),

Yes, this is a nice code. Asymptote has several nice commands to cut curves and surfaces. In some sense, though, this solution is also not completely automatic because one has to cut the circle into its visible and hidden pieces by hand. (The `fillbetween` library of pgfplots also has some means to decompose curves into their intersection segments, but I think that as of now these tools are somewhat less powerful and less precise than their `asymptote` and `metapost` counterparts.)

An answer [here](https://tex.stackexchange.com/questions/481283/intersection-of-a-sphere-and-a-plane-knowing-equations/569030#569030) about intersection of a plane and a sphere, where the cross section boundary is split automatically into the front and the back curves.

I have `asymptote` or `Asympote` installed. However, my installation does not have the `macros3D.asy` file. It does have all the other libraries which you load with `import`. I also checked that it is not contained in the archive on https://sourceforge.net/projects/asymptote/ (I think). You can find the official libraries at https://github.com/vectorgraphics/asymptote/tree/master/base.

I copy a code at here. This is not my code ```settings.render=0; import three; import math; import solids; import macros3D; size(5cm); currentprojection=orthographic(.7,0,0.5); defaultpen(fontsize(8pt)); dotfactor =3; pen An=linetype("5 5"); real r=2, ang=40, h=2.5; triple S=h*Z, A=0*X,C=r/Cos(ang)*Y, B=(r*Sin(ang),r*Cos(ang),0); draw(S--A^^S--B^^S--C); draw(A--C,An); draw(A--B--C); real kB = intersect(S,B,(B-S),A); triple H = (1-kB)*S+kB*B; dot(H,red); //---- Dung hinh chieu cua A len SC real kC = intersect(S,C,(C-S),A); triple K = (1-kC)*S+kC*C; dot(K,blue); draw(A--K,An); draw(H--K); draw(A--H); real bkGoc=2.5; drawrightangle(H,A,S,radius=bkGoc*mm); drawrightangle(K,A,S,radius=bkGoc*mm); drawrightangle(B,C,A,radius=bkGoc*mm); drawrightangle(A,B,S,radius=bkGoc*mm); triple I=C/2+H/2,J=A/2+K/2; real ra=abs(C-H)/2,rb=abs(A-K)/2; path3 p=B--C--H--cycle, q=A--H--K--cycle, ca=circle(I,ra,normal(p)), cb=circle(J,rb,normal(q)); draw(ca); path p1=cut(project(cb),project(A--S--K),1).before, p2=cut(project(cb),project(A--S--K),2).after, p=cut(cut(project(cb),project(A--S--K),1).after, project(A--S--K),1).before; //----------------------------- draw(invert(p1,Z,O),blue); draw(invert(p2,Z,O),red); draw(invert(p,Z,O),An+green); dot("$A$",A,dir(180));dot("$B$",B,dir(-90)); dot("$C$",C,dir(0)); dot("$S$",S,dir(90)); dot("$H$",H,dir(0)); dot("$K$",K,1.7*dir(64));```

That's very interesting! I think g.kov is an expert. If you look at the code, the dashed lines are drawn by hand, i.e. the user has to put `hidLine` and `visLine` by hand. So in this sense it is not completely off if one draws things with Ti*k*Z. So yes, I agree, it seems to be the case that one will need to write an algorithm if one wants to do this automatically. I do not think that this is very easy. In general, lines can be partially hidden and partially visible...

```import three; // 3D module import math; currentprojection=orthographic(camera=(55,144,80), up=(0,0,1),target=(0,0,0),zoom=1,center=true); size(300); size3(300,300,300); triple intersectionpoint(triple a,triple b,triple c,triple d){ real u=((d.x-c.x)*a.y+(c.y-d.y)*a.x+c.x*d.y-d.x*c.y)/ ((d.y-c.y)*b.x+(c.x-d.x)*b.y+(d.x-c.x)*a.y+(c.y-d.y)*a.x); return a*(1.0-u)+b*u; } triple A,B,C,D,EE,II,H,K,M,NN,O,SS; // S,E and N has special meaning in asy: // as South, East and North or (0,-1), (1,0) and (0,1) // and I is a sqrt(-1)=(0,1) real a=40; // side of the square; real h=50; // height, h=AS real d=sqrt(2)/2*a; // half of the diagonal O=(0,0,0); C=(0,d,0); B=(d,0,0); A=(0,-d,0); D=(-d,0,0); SS=A+(0,0,h); M=0.5(SS+A); II=0.5(SS+D); NN=intersectionpoint(SS,(SS+A-B),C,II); real phi=atan(h/a); real u=a*cos(phi)/sqrt(a^2+h^2); EE=D*(1-u)+SS*u; K=EE+B-A; real psi=atan(h/d); real u=d*cos(psi)/sqrt(d^2+h^2); H=O*(1-u)+SS*u; pair Q=intersectionpoint(project(NN--B),project(SS--D)); pen dashed=linetype(new real[] {5,5}); // set up dashed pattern pen visLine=darkblue+0.8pt; pen hidLine=lightblue+dashed+0.8pt; void Dot(...triple[] v){ dotfactor=8; for(int i=0;i<v.length;++i){ dot(project(v[i]),UnFill); } } void Draw3(guide3 g, pen p=currentpen){ draw(project(g),p); } void labelP(string s,triple t,pair p=(0,0)){ label("$"+s+"$",project(t),p); } Draw3(B--A--D,hidLine); Draw3(H--A--SS,hidLine); Draw3(M--II,hidLine); Draw3(EE--A--C,hidLine); Draw3(B--D,hidLine); Draw3(SS--O,hidLine); Draw3(SS--B--C--SS--D--C,visLine); Draw3(SS--NN--C,visLine); Draw3(EE--K--B,visLine); Draw3(NN--K,visLine); draw(project(NN)--Q,visLine); draw(project(B)--Q,hidLine); Dot(A,B,C,D,EE,H,II,K,M,NN,O,SS); labelP("A",A,NW); labelP("B",B,SW); labelP("C",C,E); labelP("D",D,NE); labelP("E",EE,NE); labelP("H",H,NE); labelP("I",II,NE); labelP("K",K,SE); labelP("M",M,W); labelP("N",NN,W); labelP("O",O,S); labelP("S",SS,NW);```

An example about asymptote. I think, we must construc functions to draw the hidden lines dashed automatically. [here](https://tex.stackexchange.com/questions/108612/how-to-draw-this-pyramid-with-tex).

I am not at all fluent in asymptote, so I think that there are better users to ask. As I am not very experienced, you should take the following statement with a grain of salt: I am not aware of any built-in feature in `asymptote` that allows the user to draw the hidden lines dashed *automatically*. However, there are asymptote experts who are able to do so, see e.g. http://www.mathematicalgemstones.com/maria/images.php. It would actually be great if such experts could contribute to this site, they seem to have an immense knowledge that they could share....

I actually have to correct myself: it seems to be not too difficult to project the texts on the triangle. ``` \documentclass[varwidth]{standalone} \usepackage{asymptote} \begin{document} \begin{asy} settings.outformat="pdf"; settings.prc=false; settings.render=0; import three; import labelpath3;//Note labelpath3 requires cyclic paths import fontsize; unitsize(1cm); size(8cm,0); currentprojection=orthographic(2,1,0.8); triple v1=(4,0,0), v2=(0,6,0), p0=(-2,-3,0); path3 pl=plane(v1,v2,p0); transform3 proj=planeproject(pl); triple pA=(1,2,4), pB=proj*pA, pC=p0+.2*v1+.2*v2, vnP=unit(cross(v1,v2)), pD=rotate(90,pC,pC+vnP)*pB; draw(surface(pl),orange); draw(Label("$\vec{v_1}$"),p0--p0+v1,1bp+blue,Arrow3(size=8)); draw(Label("$\vec{v_2}$"),p0--p0+v2,N,1bp+blue,Arrow3(size=8)); label(project("abc",v1,v2,p0+(.5,.5,0))); draw(surface(pA--pB--pC--cycle),opacity(.5)+gray,1bp+.8blue); label(project("abc",v1,v2,p0+(.5,.5,0))); dot("$A$",pA); dot("$B$",pB); dot("$C$",pC,dir(pC-pB)); triple pBpC=pC-pB,pBpA=pA-pB; label(project("abc",pBpC,pBpA,pC+(.5,.5,0))); dot("$p_0$",p0,NW); pen p=fontsize(3mm)+yellow; path3 tri=pA--pB--pC--cycle; path3 trip=pA--pC--pB--cycle; string str1="$B-A$", str2="$C-B$", str3="$C-A$"; draw(labelpath(str1,subpath(tri,0.7,0.3),angle=90,optional=rotate(270,X)*Y), p,yellow); draw(labelpath(str2,subpath(tri,1.7,1.3),angle=90,optional=rotate(270,X)*Y), p,yellow); draw(labelpath(str3,subpath(tri,2.3,2.7),angle=270,optional=rotate(270,X)*Y), p,yellow); shipout(bbox(2mm,Fill(white))); \end{asy} \end{document} ``` ![Screen Shot 2020-10-15 at 11.34.17 AM.png](/image?hash=b9386d6acbd703b3601e3749dc86e0e1e5e3b95c6f735375cb51c2dba7da9c0b) This example is not at all streamlined. However, what I failed to do is to project an external graphics. (The error message gives a hint what one could look at, but it is probably fair to say that as of now the projection of external graphics is easier with Ti*k*Z. )

As far as I know it becomes even more complicated if one wants to project an external graphics on a plane with `asymptote`. Please note that I do not say it is impossible but this question seems to stick around without any simple answer. It could well be that there is a simple solution, but I did not really see one so far.

More broadly, you can argue that for any of the packages Ti*k*Z and `pgfplots` there are external alternatives such as Mathematica or `asymptote` that allow you to generate the graphics more easily (but not necessarily if you want vector graphics). But nevertheless ti can make sense to use Ti*k*Z or `pgfplots` because you can control the graphics from within the LaTeX documents. One example is a beamer presentation in which you uncover a graph step by step. So I think that users need to make a choice that is convenient for them. This is basically one of the virtues of these Q & A sites: you may receive different answers to a give question, and this allows users to gauge which strategy suits them most. Hence I'd be interested to see `asymptote` alternatives to such questions, maybe you can persuade Black Mild to provide some.

It depends on what you want to do. `asymptote` has many 3D features built in. So you do not need to program them. However, it is an external tool, so you need to compile externally. Also there are some things that seem to be easier with Ti*k*Z such as projecting something on a plane. I am convinced that `asymptote` can do that, but I am not aware of a built-in way that does it. This is an example for which the situation is reversed, you would need to program yourself in asymptote that is already built into some standard package of Ti*k*Z. Some long time ago I tried to embed an external graphics in a 3d `asymptote` picture, and asked a question. This question did not get answered even though I awarded a large bounty. This seems to be another case of something that can be done more easily with Ti*k*Z. Yet you will find more examples of situations that can be done more easily with `asymptote`.

It is true in the sense that it does not have a built-in 3d engine. And it does, as far as I know, no built-in means to verify if a point is inside or outside of a shape, so one needs to write the function by oneself. Other tools may have this functionality built in. So far I completely agree. What I do not know is how "real 3D" is defined.

@marmot, re: [your answer](#a1660), [here](https://tex.stackexchange.com/questions/566807/how-to-plot-3d-convex-hull-using-tikz-pgf/566817#566817), Black Mild said "TikZ is not real 3D. For simple 3D figures, you can calculate yourself and ask TikZ to draw. A bit better way is using tikz-3d-plot, but it is far from real 3D. For example, in your question, to find a convex hull of 5 points, you need a procedure/function to check whether 5th point is inside the tetrahedron of the remaing 4 points or not. That is very very hard job. Computation ability of TikZ/LaTeX is quite limited! " Is this true?

1 Answer