I had some code for the circumcicle center on my computer, it is likely that it is from an answer and parts of the code come from the corresponding question. Yet I did not really find them. Anyway, here it is.
```
\documentclass[border = 3mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}
\tikzset{circumcenter/.code n args={3}{%
\path[overlay] (#1) coordinate (@a) (#2) coordinate (@b) (#3) coordinate (@c)
($(@b)!.5!(@c)$) coordinate (#1-prime)
($(@a)!.5!(@c)$) coordinate (#2-prime)
($(@a)!.5!(@b)$) coordinate (#3-prime)
($(#1-prime)!1cm!90:(@b)$) coordinate (@aaux)
($(#3-prime)!1cm!90:(@b)$) coordinate (@caux);
\tikzset{insert path={(intersection cs:first line={(#3-prime)--(@caux)},
second line={(#1-prime)--(@aaux)})}}
}}
\begin{document}
\begin{tikzpicture}[scale=1,declare function={a=5;b=12;c=10;}]
\coordinate (A) at (0,0);
\coordinate (B) at (c,0);
\coordinate (C) at ({(pow(b,2) + pow(c,2) - pow(a,2))/(2*c)},{sqrt((a+b-c) *(a-b+c) *(-a+b+c)* (a+b+c))/(2*c)});
\path[circumcenter={A}{B}{C}] coordinate (I);
\foreach \p/\g in {A/180,C/90,B/-90,I/90}
{\draw[fill=black] (\p) circle[radius=1.5pt];
\path (\p)+(\g:3mm) node{$\p$};}
\draw[thick] let \p1=($(A)-(I)$),\n1={veclen(\x1,\y1)} in (I) circle[radius=\n1];
\draw[blue] (A) -- (B) -- (C) -- cycle;
\end{tikzpicture}
\end{document}
```
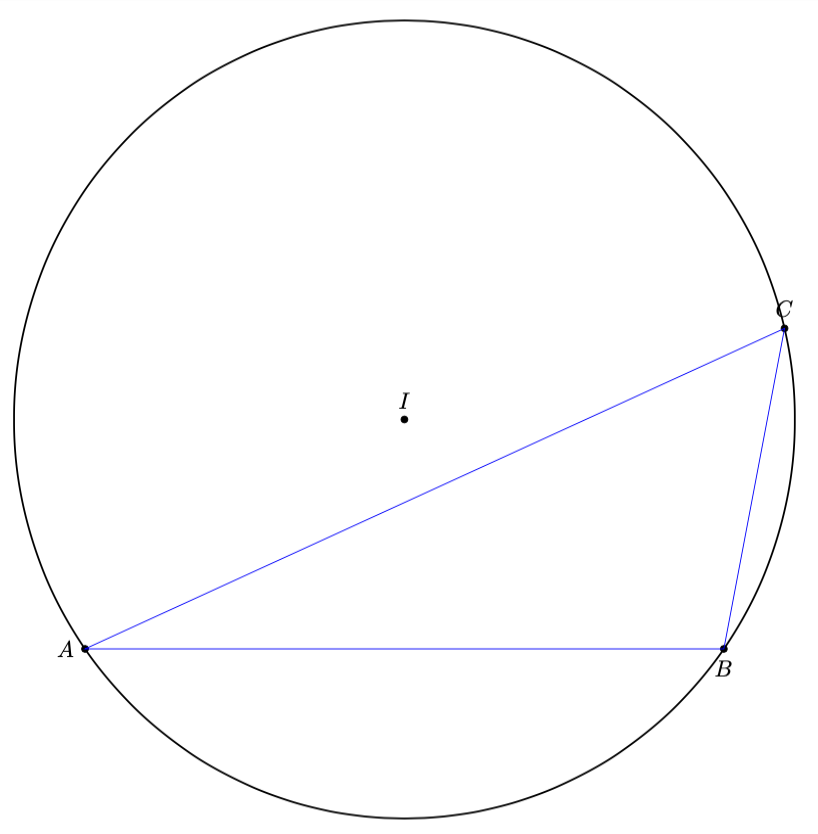
**ADDENDUM**: Here is a code that determines the triangle for three parameters, which can either be three sides, two sides and one angle or one side and two angles. It does yield the above triangle, though rotated.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{angles,calc}
\tikzset{pics/triangle/.style={code={
\tikzset{triangle pars/.cd,#1}%
\def\pv##1{\pgfkeysvalueof{/tikz/triangle pars/##1}}%
\edef\lstsides{"a","b","c"}%
\edef\lstangles{"A","B","C"}%
\def\tmpundef{undef}%
\edef\temp{\pv{a}}%
\ifx\temp\tmpundef
\edef\nsides{0}%
\else
\edef\nsides{1}%
\edef\firstside{0}%
\fi
\edef\temp{\pv{b}}%
\ifx\temp\tmpundef
\else
\edef\nsides{\the\numexpr\nsides+1}%
\ifnum\nsides=1
\edef\firstside{1}%
\else
\edef\secondside{1}%
\fi
\fi
\edef\temp{\pv{c}}%
\ifx\temp\tmpundef
\else
\edef\nsides{\the\numexpr\nsides+1}%
\ifnum\nsides=1
\edef\firstside{2}%
\else
\ifcase\nsides
\or
\edef\firstside{2}%
\or
\edef\secondside{2}%
\or
\edef\thirdside{c}%
\fi
\fi
\fi
\edef\temp{\pv{A}}%
\ifx\temp\tmpundef
\edef\nangles{0}%
\else
\edef\nangles{1}%
\edef\firstangle{0}%
\fi
\edef\temp{\pv{B}}%
\ifx\temp\tmpundef
\else
\edef\nangles{\the\numexpr\nangles+1}%
\ifnum\nangles=1
\edef\firstangle{1}%
\else
\edef\secondangle{1}%
\fi
\fi
\edef\temp{\pv{C}}%
\ifx\temp\tmpundef
\else
\edef\nangles{\the\numexpr\nangles+1}%
\ifcase\nangles
\or
\edef\firstangle{2}%
\or
\edef\secondangle{2}%
\or
\edef\thirdangle{2}%
\fi
\fi
\ifnum\numexpr\nangles+\nsides=3 % the number of input parameters is fine
\ifcase\nsides
\message{You need to specify at least one side.^^J}
\or % one side and two angles
\pgfmathsetmacro{\mysidei}{{\lstsides}[\firstside]}%
\pgfmathsetmacro{\myanglei}{{\lstangles}[\firstangle]}%
\pgfmathsetmacro{\myangleii}{{\lstangles}[\secondangle]}%
\pgfmathtruncatemacro{\thirdangle}{Mod(3-\firstangle-\secondangle,3)}%
\pgfmathsetmacro{\myangleiii}{{\lstangles}[\thirdangle]}%
\pgfmathtruncatemacro{\itest}{(\firstside==\firstangle)||(\firstside==\secondangle)}%
\ifnum\itest=0 % both angles involve known side
\draw[pic actions] (0,0)
coordinate[label=below:$\pv{\myangleii}$] (-B)
-- node[midway,auto]{$\mysidei=\pv{\mysidei}$}
(\pv{a},0) coordinate (-C)
--
(intersection cs:first line={(-B)--($(-B)+({\pv{\myangleii}}:1)$)},
second line={(-C)--($(-C)+({-180+\pv{\myanglei}}:1)$)})
coordinate (-A) -- cycle;
\else % one angle is away from the known side
\ifnum\firstside=\firstangle
\draw[pic actions] (0,0)
coordinate[label=below:$\myangleii$] (-\myangleii)
-- node[midway,auto]{$\mysidei=\pv{\mysidei}$}
(\pv{a},0) coordinate[label=below:$\myangleiii$] (-\myangleiii)
--
(intersection cs:first line={(-\myangleii)--($(-\myangleii)+({\pv{\myangleii}}:1)$)},
second line={(-\myangleiii)--($(-\myangleiii)+({-180+\pv{\myanglei}+\pv{\myangleii}}:1)$)})
coordinate[label=above:$\myanglei$] (-\myanglei) -- cycle
($(-\myangleii)+(0:\pv{r})$)arc[start angle=0,end angle=\pv{\myangleii},radius=\pv{r}]
($(-\myanglei)+(180+\pv{\myangleii}:\pv{r})$)
arc[start angle=180+\pv{\myangleii},end angle=180+\pv{\myanglei}+\pv{\myangleii},radius=\pv{r}]
;
\else
\draw[pic actions] (0,0)
coordinate[label=below:$\myanglei$] (-\myanglei)
-- node[midway,auto]{\mysidei}
(\pv{a},0) coordinate[label=below:$\myangleiii$] (-\myangleiii)
--
(intersection cs:first line={(-\myanglei)--($(-\myanglei)+({\pv{\myanglei}}:1)$)},
second line={(-\myangleiii)--($(-\myangleiii)+({-180+\pv{\myanglei}+\pv{\myangleii}}:1)$)})
coordinate[label=above:$\myangleii$] (-\myangleii) -- cycle
($(-\myanglei)+(0:\pv{r})$)arc[start angle=0,end angle=\pv{\myanglei},radius=\pv{r}]
($(-\myangleii)+(180+\pv{\myanglei}:\pv{r})$)
arc[start angle=180+\pv{\myanglei},end angle=180+\pv{\myanglei}+\pv{\myangleii},radius=\pv{r}]
;
\fi
\fi
\or % two sides and one angle
\pgfmathsetmacro{\mysidei}{{\lstsides}[\firstside]}%
\pgfmathsetmacro{\mysideii}{{\lstsides}[\secondside]}%
\pgfmathsetmacro{\myanglei}{{\lstangles}[\firstangle]}%
\pgfmathtruncatemacro{\thirdside}{Mod(3-\firstside-\secondside,3)}%
\pgfmathsetmacro{\mysideiii}{{\lstsides}[\thirdside]}%
\pgfmathsetmacro{\myangleii}{{\lstangles}[\secondside]}%
\pgfmathsetmacro{\myangleiii}{{\lstangles}[\thirdside]}%
\pgfmathtruncatemacro{\itest}{(\firstside==\firstangle)||(\secondside==\firstangle)}%
\ifnum\itest=0 % both sides attach to the angle
\pgfmathsetmacro{\myangleii}{{\lstangles}[\firstside]}%
\pgfmathsetmacro{\myangleiii}{{\lstangles}[\secondside]}%
\draw[pic actions] (\pv{\myanglei}:\pv{\mysidei})
coordinate[label=above:$\myangleiii$] (-\myangleiii)
-- node[midway,auto]{$\mysidei=\pv{\mysidei}$}
(0,0) coordinate[label=below:$\myanglei$] (-\myanglei)
-- node[midway,auto]{$\mysideii=\pv{\mysideii}$}
(\pv{\mysideii},0) coordinate[label=below:$\myangleii$] (-\myangleii)
-- cycle
(\pv{r},0) arc[start angle=0,end angle=\pv{\myanglei},radius=\pv{r}];
\else
\pgfmathsetmacro{\mya}{max(\pv{\mysidei},\pv{\mysideii})}%
\pgfmathsetmacro{\myb}{min(\pv{\mysidei},\pv{\mysideii})}%
\pgfmathsetmacro{\myc}{\myb*cos(\pv{\myanglei})%
+sqrt(\mya*\mya-pow(\myb*sin(\pv{\myanglei}),2)}%
\ifnum\firstside=\firstangle
\draw[pic actions] (\pv{\myanglei}:\myc)
coordinate[label=above:$\myangleii$] (-\myangleii)
-- (0,0) coordinate[label=below:$\myanglei$] (-\myanglei)
-- node[midway,auto]{$\mysideii=\pv{\mysideii}$}
(\pv{\mysideii},0) coordinate[label=below:$\myangleiii$] (-\myangleiii)
-- node[midway,auto]{$\mysidei=\pv{\mysidei}$} cycle
(\pv{r},0) arc[start angle=0,end angle=\pv{\myanglei},radius=\pv{r}];
\else
\pgfmathsetmacro{\myangleii}{{\lstangles}[\thirdside]}%
\pgfmathsetmacro{\myangleiii}{{\lstangles}[\firstside]}%
\draw[pic actions] (\pv{\myanglei}:\myc)
coordinate[label=above:$\myangleiii$] (-\myangleiii)
-- (0,0) coordinate[label=below:$\myanglei$] (-\myanglei)
-- node[midway,auto]{$\mysidei=\pv{\mysidei}$}
(\pv{\mysidei},0) coordinate[label=below:$\myangleii$] (-\myangleii)
-- node[midway,auto]{$\mysideii=\pv{\mysideii}$} cycle
(\pv{r},0) arc[start angle=0,end angle=\pv{\myanglei},radius=\pv{r}];
\fi
\fi
\or %three sides
%\typeout{3 sides}
\pgfmathsetmacro{\mymax}{max(\pv{a},\pv{b},\pv{c})}%
\pgfmathtruncatemacro{\itest}{sign(2*\mymax-\pv{a}-\pv{b}-\pv{c})}%
\ifnum\itest<1
\draw[pic actions] (0,0) coordinate[label=below:$B$] (-B)
-- node[midway,auto]{$a=\pv{a}$}
(\pv{a},0) coordinate[label=below:$C$] (-C)
-- node[midway,auto]{$b=\pv{b}$}
(intersection cs:first line={(-B)--($(-B)+({cosinelaw(\pv{a},\pv{c},\pv{b})}:1)$)},
second line={(-C)--($(-C)+({-cosinelaw(\pv{a},\pv{b},\pv{c})}:1)$)})
coordinate[label=above:$A$] (-A) --
node[midway,auto]{$c=\pv{c}$} cycle;
\else
\message{a=\pv{a},b=\pv{b},c=\pv{c} is not consistent since one side is
longer than the sum of two other sides.^^J}
\fi
\fi
\else
\message{Incorrect input. You need to specify three parameters.^^J}
\fi
}},
declare function={cosinelaw(\a,\b,\c)=acos((\a*\a+\b*\b-\c*\c)/(2*\a*\b));},
triangle pars/.cd,
A/.initial=undef,B/.initial=undef,C/.initial=undef,% angles
a/.initial=undef,b/.initial=undef,c/.initial=undef,% sides
r/.initial=1%radius of angles
}
\begin{document}
\begin{tikzpicture}[scale=1,declare function={a=5;b=12;c=10;}]
\pic{triangle={a=a,b=b,c=c}};
\end{tikzpicture}
\end{document}
```
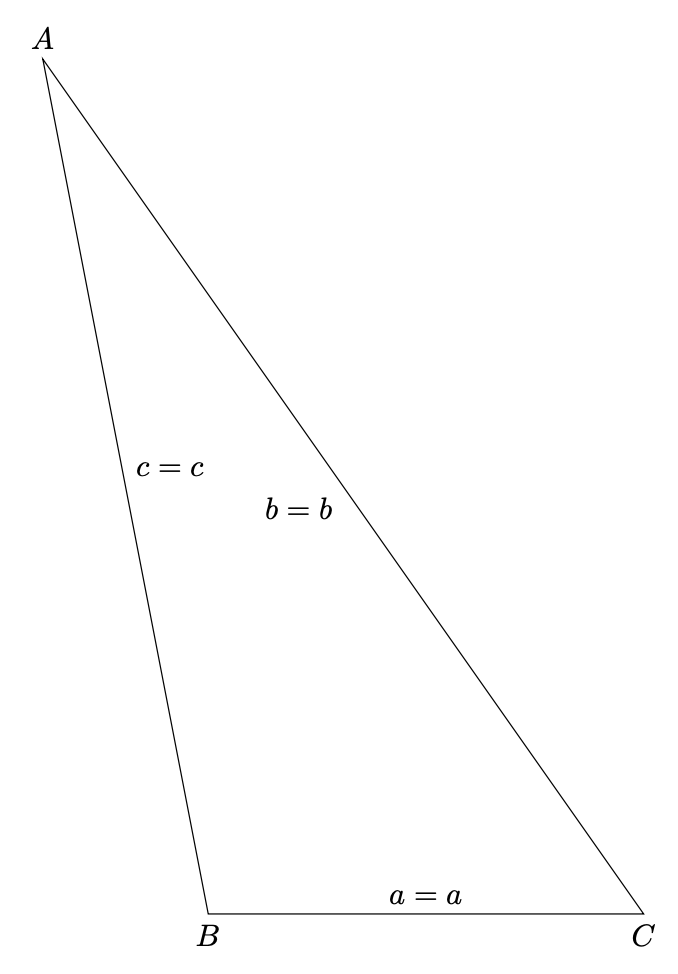
As usual one can make things more versatile. However this would essentially amount to writing a package for 2D Euclidean geometry. Such a package already exists (`tkz-euclide`) and I think another one is in preparation by Joule V and collaborators. So I am not going to mess with this. :smile_cat: