How to get correct dashed lines of two cylinders like this picture? - TeX

TopAnswers TeX

Top Answer

user 3.14159

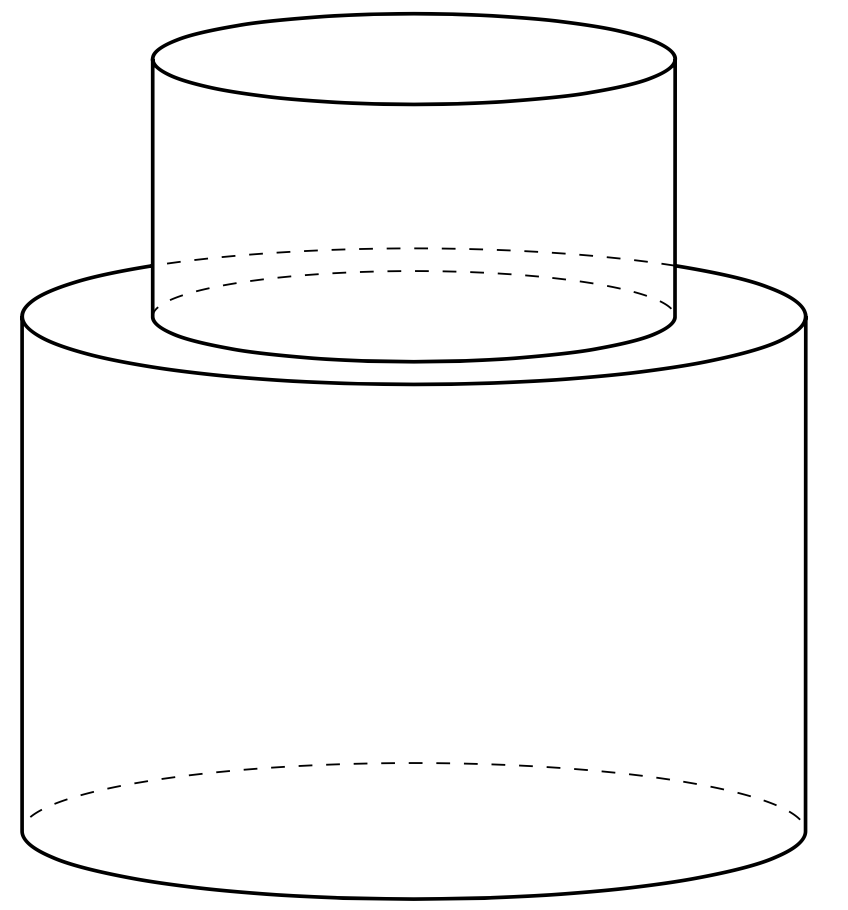
You already determined the critical angle for single cylinders. There is only one more critical angle which determines which fraction of the larger cylinder is covered by the smaller one. In the case at hand, this is just the `arcsin` of the ratio `r/R` plus some stuff that depends on the view angle `phi`. In more complicated settings you could work with clips and reverse clips, but here it is easier to work with the analytic solution.

```
\documentclass[border=1mm,tikz]{standalone} 
\usepackage{tikz-3dplot} 
\begin{document} 
\tdplotsetmaincoords{80}{70}
\begin{tikzpicture}[tdplot_main_coords,
	visible/.style={thick},hidden/.style={dashed},
	declare	function={H=4;h=2;R=3;r=2;phi1=\tdplotmainphi;
		phi2=\tdplotmainphi+180;phi3=\tdplotmainphi-180;
		phi4=\tdplotmainphi+90+asin(r/R);
		phi5=\tdplotmainphi+90-asin(r/R);
		}] 
 \path (0,0,H) coordinate(M) (0,0,H+h) coordinate(m)
	({R*cos(phi1)},{R*sin(phi1)},0 ) coordinate (BL)
	({R*cos(phi2)},{R*sin(phi2)},0 ) coordinate	(BR)
	({R*cos(phi1)},{R*sin(phi1)},H ) coordinate (TL)
	({R*cos(phi2)},{R*sin(phi2)},H ) coordinate	(TR)
	({r*cos(phi1)},{r*sin(phi1)},H ) coordinate (bl)
	({r*cos(phi2)},{r*sin(phi2)},H ) coordinate	(br)
	({r*cos(phi1)},{r*sin(phi1)},H+h) coordinate (tl)
	({r*cos(phi2)},{r*sin(phi2)},H+h) coordinate (tr);
  \begin{scope}[canvas is xy plane at z=0]
   \draw[hidden] (br) arc[start angle=phi3,end angle=phi2,radius=r]
    (BR) arc[start angle=phi3,end angle=phi2,radius=R]
	($(M)+(phi5:R)$) arc[start angle=phi5,end angle=phi4,radius=R];
   \draw[visible] (tr) -- (br) 
   	arc[start angle=phi3,end angle=phi1,radius=r] -- (tl)
	(m) circle[radius=r]
	(TR) -- (BR) arc[start angle=phi3,end angle=phi1,radius=R] -- (TL)
	($(M)+(phi5:R)$) arc[start angle=phi5,end angle=phi4-360,radius=R];
  \end{scope} 	
\end{tikzpicture}
\end{document}
```

![Screen Shot 2020-09-26 at 7.59.38 PM.png](/image?hash=37640f8a32ebbdb8805b6c2465258655add8c14c28789a47d05fead094500f0f)

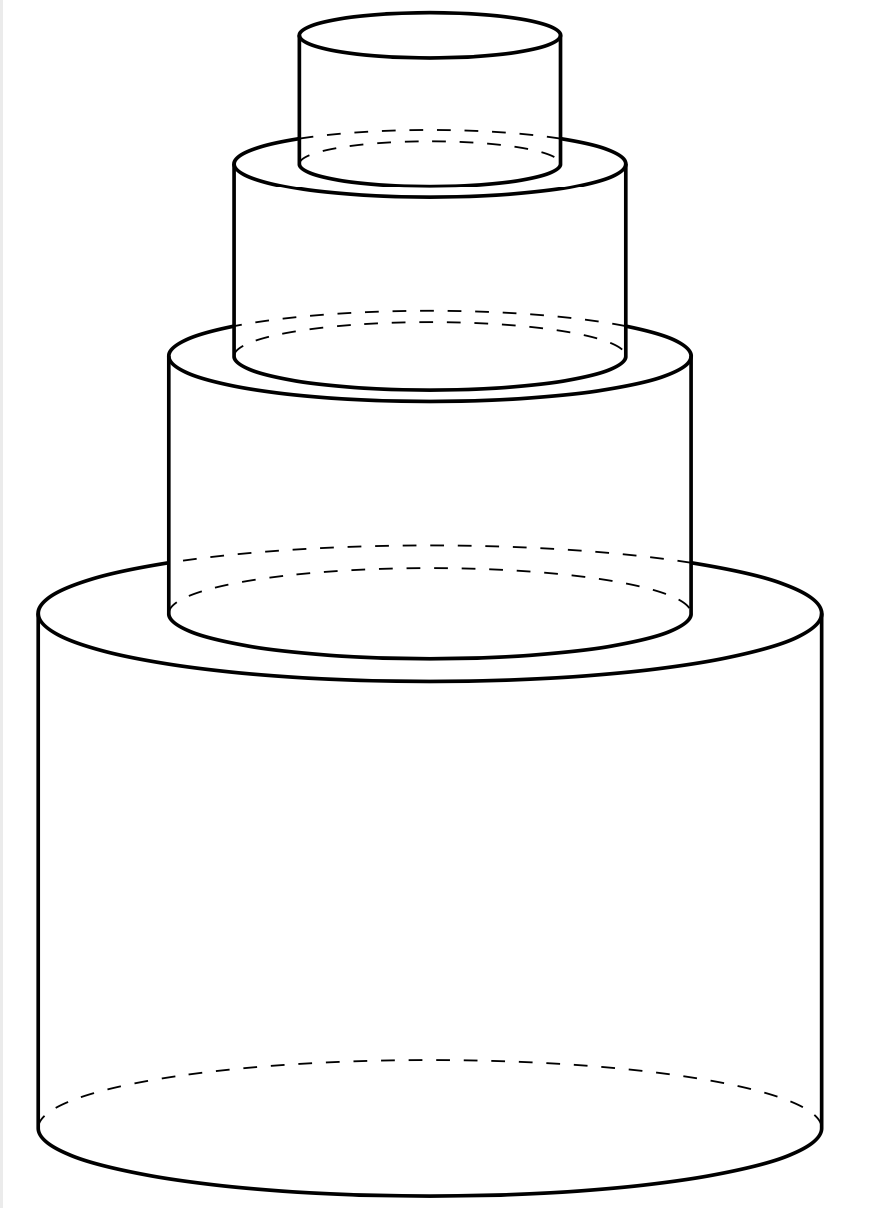
You can iterate this in a loop. The heights and radii are stored in the lists `lH` and `lR`, respectively.

```
\documentclass[border=1mm,tikz]{standalone} 
\usepackage{tikz-3dplot} 
\begin{document} 
\tdplotsetmaincoords{80}{70}
\begin{tikzpicture}[tdplot_main_coords,
	visible/.style={thick},hidden/.style={dashed},
	declare	function={lH={4,2,1.5,1};% list of heights
	    lR={3,2,1.5,1};% list of radii
	    phi0=\tdplotmainphi+90;
		phihid(\r,\R)=asin(\r/\R);
		}] 
 \pgfmathtruncatemacro{\mydim}{dim(lH)-1}	
 \pgfmathsetmacro{\myh}{0}
 \path (0,0,\myh) coordinate (M0);
 \foreach \X [remember=\myh as \myh,count=\Y] in {0,...,\mydim}
 {\pgfmathsetmacro{\myh}{\myh+{lH}[\X]}
  \pgfmathsetmacro{\myr}{{lR}[\X]}
  \path (0,0,\myh) coordinate (M\Y);
  \begin{scope}[canvas is xy plane at z=0]
   \draw[hidden] ($(M\X)+(phi0+90:\myr)$) 
		arc[start angle=phi0+90,end angle=phi0-90,radius=\myr];
   \draw[visible] ($(M\Y)+(phi0-270:\myr)$)
	  -- ($(M\X)+(phi0-270:\myr)$)
	  arc[start angle=phi0-270,end angle=phi0-90,radius=\myr]
	  -- ($(M\Y)+(phi0-90:\myr)$);
   \ifnum\X=\mydim
    \draw[visible] (M\Y) circle[radius=\myr]; 
   \else
    \pgfmathsetmacro{\myphicrit}{phihid({lR}[\Y],\myr)}
	\draw[hidden] ($(M\Y)+(phi0-\myphicrit:\myr)$)
	  arc[start angle=phi0-\myphicrit,end angle=phi0+\myphicrit,radius=\myr];
	\draw[visible] 
	  ($(M\Y)+(phi0-\myphicrit:\myr)$)
	  arc[start angle=phi0-\myphicrit,end angle=phi0+\myphicrit-360,radius=\myr];
   \fi
  \end{scope}
 }
\end{tikzpicture}
\end{document}
```

![Screen Shot 2020-09-26 at 9.07.34 PM.png](/image?hash=da85348003e6898291d404c790e6ed1d65941b570a78db59dd35e8396736ec60)

Yes. ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools \begin{document} \begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,line join=round,c/.style={circle,fill,inner sep=1pt}, declare function={r=3;h=3;myr=3;}] \pic{3d/frustum={R=r,r=r,h=r}}; \path (0,0,0) coordinate (O) (0,0,h) coordinate (O'); \draw[3d/hidden] (O) -- (O'); \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1603), Sometimes, I draw a cylinder step by step. This is my try ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,3dtools}% https://github.com/marmotghost/tikz-3dtools \begin{document} \begin{tikzpicture}[3d/install view={phi=70,theta=70},scale=1,line cap=butt,line join=round,c/.style={circle,fill,inner sep=1pt}, declare function={r=3;h=3;myr=3;}] \path (0,0,0) coordinate (O) (0,0,h) coordinate (O'); \draw[3d/visible] (O') circle[radius=myr] ([xshift=-myr*1cm]O) -- ([xshift=-myr*1cm]O') ([xshift=myr*1cm]O) -- ([xshift=myr*1cm]O'); \path pic{3d/circle on sphere={R=myr,C={(0,0,0)},P={(0,0,0)},n={(0,0,1)}}}; \path foreach \p/\g in {O'/90,O/-90} {(\p)node[c]{}+(\g:2.5mm) node{$\p$}}; \draw[3d/hidden] (O) -- (O'); \end{tikzpicture} \end{document} ``` Can it be simpler?

I tried ``` \documentclass[border=1mm,12pt,tikz]{standalone} \usetikzlibrary{3dtools} \begin{document} \foreach \Angle in {5,10,...,60} {\begin{tikzpicture}[3d/install view={phi=\Angle,psi=0,theta=70}, line join = round, line cap = round,same bounding box=A, declare function={h=4;myr=1;}] \path (0,0,0) coordinate (O) (-1,-1,0) coordinate (A) (2,-1,0) coordinate (B) (-1,3,0) coordinate (C) (0,0,h) coordinate (O') (-1,-1,h) coordinate (A') (2,-1,h) coordinate (B') (-1,3,h) coordinate (C') (0,0,h/2) coordinate (O''); \tikzset{3d/polyhedron/.cd,O={(O'')}, fore/.append style={fill=none,/tikz/3d/visible}, back/.append style={fill=none,/tikz/3d/hidden}, draw face with corners={{(A)},{(B)},{(B')},{(A')}}, draw face with corners={{(B)},{(C)},{(C')},{(B')}}, draw face with corners={{(C)},{(A)},{(A')},{(C')}}, draw face with corners={{(A')},{(B')},{(C')}}} \draw[3d/hidden,3d/screen coords] (-myr,0|-O) -- (-myr,0|-O') (myr,0|-O) -- (myr,0|-O') ; \draw[3d/visible] (O') circle[radius=myr]; \draw[3d/hidden] (O) circle[radius=myr]; \end{tikzpicture}} \end{document} ```

It draws the dashed part of the cylinder. We know that the width of the projection of the cylinder is 2*radius centered around the axis, and that the axis is in the vertical direction, so we can use `xshift`.

``` \documentclass[border=1mm,12pt,tikz]{standalone} \usetikzlibrary{3dtools} \begin{document} \foreach \Angle in {5,15,...,355} {\begin{tikzpicture}[3d/install view={phi=\Angle,psi=0,theta=70}, line join = round, line cap = round,same bounding box=A, declare function={h=4;myr=1;}] \path (0,0,0) coordinate (O) (-1,-1,0) coordinate (A) (2,-1,0) coordinate (B) (-1,3,0) coordinate (C) (0,0,h) coordinate (O') (-1,-1,h) coordinate (A') (2,-1,h) coordinate (B') (-1,3,h) coordinate (C') (0,0,h/2) coordinate (O''); \tikzset{3d/polyhedron/.cd,O={(O'')}, fore/.append style={fill=none,/tikz/3d/visible}, back/.append style={fill=none,/tikz/3d/hidden}, draw face with corners={{(A)},{(B)},{(B')},{(A')}}, draw face with corners={{(B)},{(C)},{(C')},{(B')}}, draw face with corners={{(C)},{(A)},{(A')},{(C')}}, draw face with corners={{(A')},{(B')},{(C')}}} \draw[3d/hidden] (O) circle[radius=myr] ([xshift=-myr*1cm]O) -- ([xshift=-myr*1cm]O') ([xshift=myr*1cm]O) -- ([xshift=myr*1cm]O'); \draw[3d/visible] (O') circle[radius=myr]; \end{tikzpicture}} \end{document} ``` ![ani.gif](/image?hash=dcd6ea4fad247f8079d4626f3e4214fcec8f8c2abd6eaabf04819a69b1792754)

@marmot, re: [your answer](#a1603), This is a cylinder is inscribed in a prism. ``` \documentclass[border=1mm,12pt,tikz]{standalone} \usetikzlibrary{calc,3d,angles} \usepackage{tikz-3dplot} \usetikzlibrary{intersections,calc,backgrounds} \usepackage{fouriernc} \begin{document} \def\a{4}% \def\R{4}% \def\h{4}% \pgfmathsetmacro{\myr}{1} \foreach \X in {10,20,...,350} {\tdplotsetmaincoords{70}{\X} \begin{tikzpicture}[tdplot_main_coords,line join = round, line cap = round] \begin{scope}[canvas is xy plane at z=0] \coordinate (O) at (0,0); \coordinate (A) at (-1, -1); \coordinate (B) at (2, -1); \coordinate (C) at (-1, 3); \draw[dashed] (\tdplotmainphi:\myr) arc(\tdplotmainphi:\tdplotmainphi+180:\myr); \draw[dashed] (\tdplotmainphi:\myr) coordinate(BR) arc(\tdplotmainphi:\tdplotmainphi-180:\myr) coordinate(BL); \end{scope} \begin{scope}[canvas is xy plane at z=\h] \coordinate (O') at (0,0); \coordinate (A') at (-1, -1); \coordinate (B') at (2, -1); \coordinate (C') at (-1, 3); \draw [dashed](BR) -- (\tdplotmainphi:\myr) (BL) -- (\tdplotmainphi-180:\myr); % vẽ hai đường sinh \draw[thick] (\tdplotmainphi:\myr) arc(\tdplotmainphi:\tdplotmainphi+180:\myr); \draw[thick] (\tdplotmainphi:\myr) coordinate(BR) arc(\tdplotmainphi:\tdplotmainphi-180:\myr) coordinate(BL); \draw [thick](BR) -- (\tdplotmainphi:\myr) (BL) -- (\tdplotmainphi-180:\myr); % vẽ hai đường sinh \end{scope} \foreach \v/\position in { B/below,O/right,A/left,B'/above,O'/right,A'/above,C/below,C'/above} {\draw[draw =black, fill=black] (\v) circle (1pt) node [\position=0.2mm] {$\v$}; } \draw[dashed] (O) -- (O') (B) --(A) --(C) (A) -- (A'); \draw[thick] (A') --(B') -- (C')-- cycle (B) -- (B') (C) -- (C'); \draw[thick] (B) -- (C) ; \node[anchor=north east] at (current bounding box.north east) {$\theta=\tdplotmaintheta^\circ,\phi=\tdplotmainphi^\circ$}; \end{tikzpicture}} \end{document} ``` How to draw in `3dtools`?

1 Answer