At [here](https://topanswers.xyz/tex?q=1233), I used Mathematica to find four vertices of a tetrahedron and draw Circumscribed sphere. Now I try to draw circumscribed sphere a tetrahedron knowing length of six edges. How can I do this?
The six edges do not specify the tetrahedron uniquely. Apart from the orientation in 3d, you'd also make one discrete choice. So I need to make some assumptions. The lengths of the edges are stored in functions on `l1`, `l2` etc.
1. The first three vertices are taken to be in the xy plane. The first edge is along the x axis. This fixes the orientation of the tetrahedron up to discrete choices (signs).
2. The fourth vertex is computed as the intersection of three spheres of radii `l4`, `l5` and `l6` using a pgf version [this code](https://stackoverflow.com/a/18654302).
The `3dtools` is in principle prepared to deal with arbitrary orientations. However, this would require more input from your side. As long as you only draw the tetrahedron, you do not have to worry about this because you can adjust the view to get the orientation you want (but there are still discrete choices). An improved version of the code that draws a face may go into the `3dtools` library so that one could, at some point, draw arbitrary polyhedra.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
% \usetikzlibrary{backgrounds}
\makeatletter
% something like this may go into the 3dtools library
\tikzset{3d/.cd,polyhedron/.cd,
draw face with corners/.code={\begingroup\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\pgfmathsetmacro\pgfutil@tmpT{TD("\pgfutil@tmpa")}%
\ifcase\c@pgf@counta
\pgfmathsetmacro\pgfutil@tmpA{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpB{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpC{TD("\pgfutil@tmpa")}%
\fi
\advance\c@pgf@counta by1\relax
\ifnum\c@pgf@counta=1\relax
\edef\pgfutil@tmpl{(\pgfutil@tmpT)}%
\else
\edef\pgfutil@tmpl{\pgfutil@tmpl -- (\pgfutil@tmpT)}%
\fi
}%
\ifnum\c@pgf@counta<3\relax
\typeout{A face needs at least three vertices. However, only \the\c@pgf@counta\space vertices were specified.}%
\else
\edef\pgfutil@tmpO{\pgfkeysvalueof{/tikz/3d/polyhedron/O}}%
\pgfmathsetmacro\pgfutil@tmpO{TD("\pgfutil@tmpO")}%
\edef\pgfutil@tmpL{\pgfkeysvalueof{/tikz/3d/polyhedron/L}}%
\pgfmathsetmacro\pgfutil@tmpL{TD("\pgfutil@tmpL")}%
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpC)-(\pgfutil@tmpA)")}%
\pgfmathsetmacro{\pgfutil@tmpc}{TD("(\pgfutil@tmpA)-(\pgfutil@tmpO)")}%
\pgfmathtruncatemacro{\pgfutil@tmpd}{sign(TD("(\pgfutil@tmpb)o(\pgfutil@tmpc)"))}%
\ifnum\pgfutil@tmpd=-1\relax
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpA)-(\pgfutil@tmpC)")}%
\fi
\pgfmathsetmacro{\pgfutil@tmpe}{screendepth(\pgfutil@tmpb)}%
\pgfmathsetmacro{\pgfutil@tmpf}{sqrt(TD("(\pgfutil@tmpb)o(\pgfutil@tmpb)"))}%
\pgfmathsetmacro{\pgfutil@tmpg}{sqrt(TD("(\pgfutil@tmpL)o(\pgfutil@tmpL)"))}%
% \typeout{polyhedron face}
% \typeout{(A)=\pgfutil@tmpA,(B)=\pgfutil@tmpB,(C)=\pgfutil@tmpC}
% \typeout{(N)=\pgfutil@tmpb}
% \typeout{b=\pgfutil@tmpb,f=\pgfutil@tmpf,g=\pgfutil@tmpg}
% \typeout{boundary: \pgfutil@tmpl}
\pgfmathsetmacro{\pgfutil@tmph}{TD("(\pgfutil@tmpL)o(\pgfutil@tmpb)")/\pgfutil@tmpf/\pgfutil@tmpg}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{70+30*\pgfutil@tmph}%
% \typeout{(\pgfutil@tmpb),\pgfutil@tmpe}
\ifdim\pgfutil@tmpe pt<0pt\relax
\else
\draw[fill=tikz@td@face@color!\pgfutil@tmpi!black] \pgfutil@tmpl -- cycle;
\fi
\fi
\endgroup
},
color/.code={\colorlet{tikz@td@face@color}{#1}},color=yellow,
O/.initial={(0,0,0)},% point inside the polyhedron
L/.initial={(1,1,1)},% "light source"
}
% temporary
% conceivably a more developed version will go into 3dtools
\tikzset{pics/generic tetrahedron/.style={code={\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\ifcase\c@pgf@counta
\edef\pgfutil@tmpA{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpB{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpC{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpD{\pgfutil@tmpa}%
\fi
\advance\c@pgf@counta by1\relax
}%
% \typeout{A=\pgfutil@tmpA,B=\pgfutil@tmpB,C=\pgfutil@tmpC,D=\pgfutil@tmpD}
\ifnum\c@pgf@counta=4\relax
\tikzset{3d/polyhedron/.cd,
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpC}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpC},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpB},{\pgfutil@tmpC},{\pgfutil@tmpD}}
}
\else
\typeout{A tetrahedron needs 4 vertices. However, you specified \the\c@pgf@counta\space vertices.}%
\fi
}}}
\makeatother
\begin{document}
\begin{tikzpicture}[scale=3,
dot/.style={circle,inner sep=1pt,fill},
declare function={l1=1;l2=1.1;l3=1.2;l4=1.3;l5=1.4;l6=1;}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=100,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos((l3*l3-l1*l1-l2*l2)/(2*l1*l2))}
\path (0,0,0) coordinate (v1)
(l1,0,0) coordinate (v2)
({l2*cos(\mytheta)},{l2*sin(\mytheta)},0) coordinate (v3);
% we do not need this here but in principle 3dtools is prepared to
% deal with arbitrarily oriented tetrahedra.
% \path[overlay,3d/define orthonormal dreibein={A={(v1)},B={(v2)},C={(v3)}}];
% however, the following works for the above input
% this is a dictionary for the code at https://stackoverflow.com/a/18654302
\tikzset{declare function={d=l1;i=l2*cos(\mytheta);j=l2*sin(\mytheta);
r1=l4;r2=l5;r3=l6;}}
\pgfmathsetmacro{\myx}{(r1*r1-r2*r2+d*d)/(2*d)}
\pgfmathsetmacro{\myy}{(r1*r1-r3*r3+2*i*\myx+j*j)/(2*j)}
\pgfmathsetmacro{\tmp}{r1*r1-\myx*\myx-\myy*\myy}
\ifdim\tmp pt<0pt
\typeout{Spheres do not intersect.}
\else
\pgfmathsetmacro{\myz}{sqrt(\tmp)}
\path (\myx,\myy,\myz) coordinate (v4);
\fi
% an educated guess for a coordinate inside the polyhedron
\path[overlay,3d coordinate={(O')=0.25*(v1)+0.25*(v2)+0.25*(v3)+0.25*(v4)}];
\path[3d/polyhedron/O={(O')}] pic[transform shape]{%
generic tetrahedron={{(v1)},{(v2)},{(v3)},{(v4)}}};
\path[3d/circumsphere center={A={(v1)},B={(v2)},C={(v3)},D={(v4)}}]
coordinate (I);
\end{scope}
% radius
\pgfmathsetmacro{\csr}{sqrt(TD("(v1)-(I)o(v1)-(I)"))}
% check radius
\foreach \XX in {1,...,4}
{\pgfmathsetmacro{\csr}{sqrt(TD("(v\XX)-(I)o(v\XX)-(I)"))}
\typeout{\csr}}
\draw[ball color=gray,fill opacity=0.2] (I) circle[radius=\csr];
% \path foreach \X in {1,...,4}
% {(v\X) coordinate[dot,label=above:{$v_\X$}]}
% (I) (I) coordinate[dot,label=above:{$I=\pgfmathparse{TD("(I)")}%
% (\pgfmathprintvector\pgfmathresult)^T$}];
\end{tikzpicture}
\end{document}
```
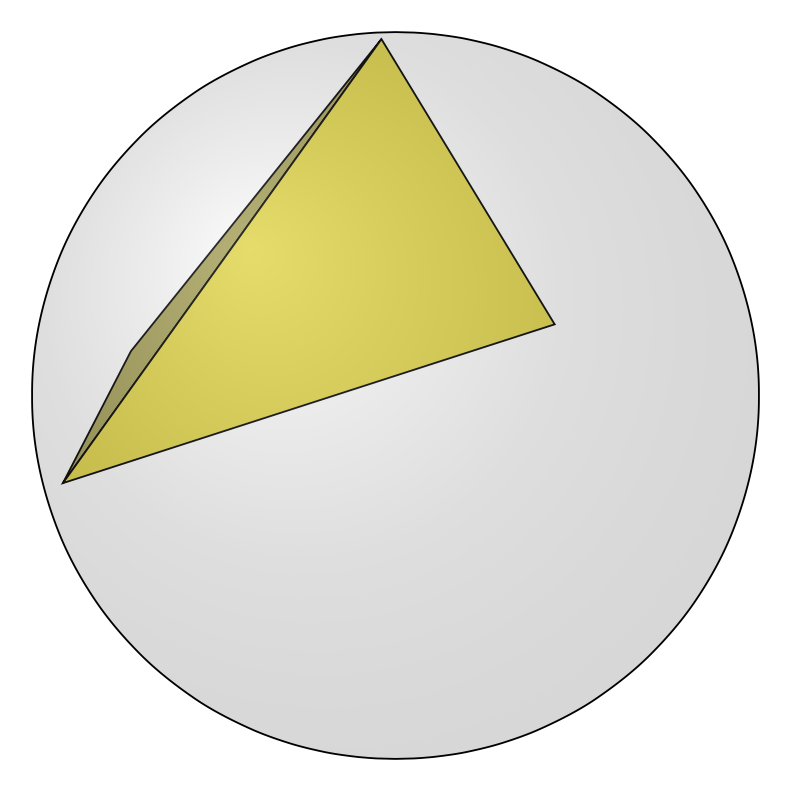
This can be animated as usual.
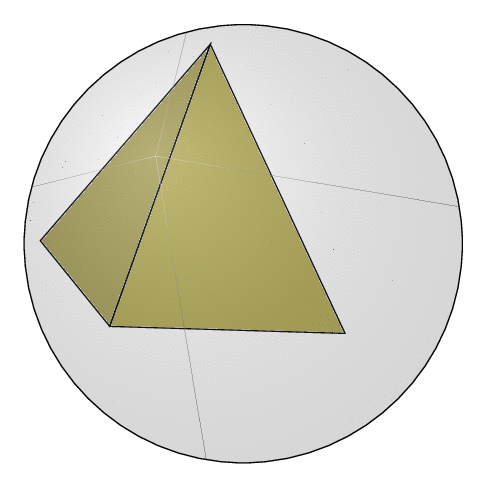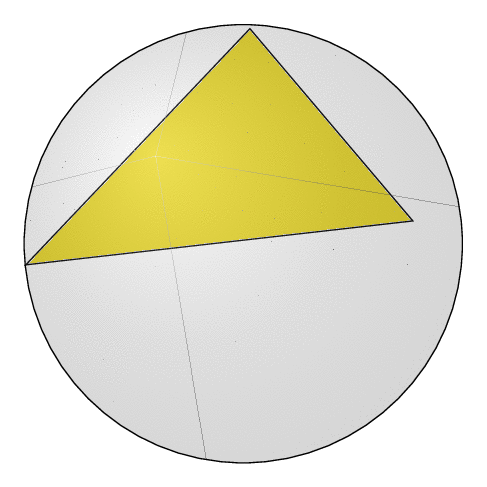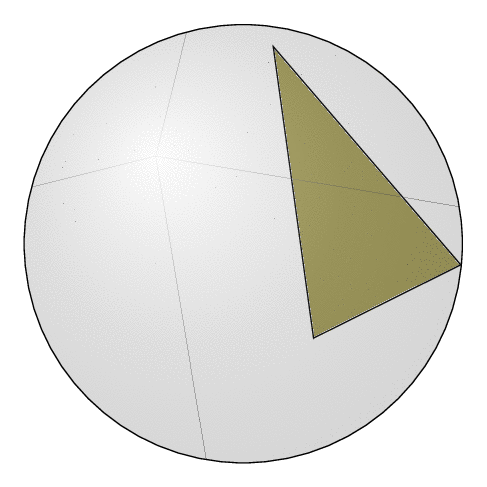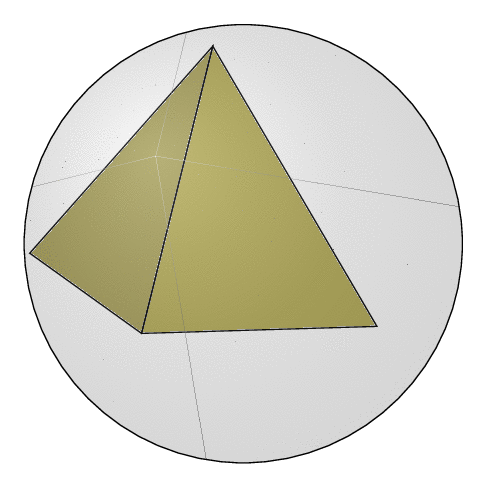
Temporary addendum: this code is merely to test things. I uses (but does not yet rely on) an addendum to the library `3dtools`: `intersection of three spheres`. I plan to add the polyhedron face style at a given point when it is clearer what the expected functionality is.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\usetikzlibrary{backgrounds}
\makeatletter
% something like this may go into the 3dtools library
\tikzset{3d/.cd,polyhedron/.cd,
draw face with corners/.code={\begingroup\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\pgfmathsetmacro\pgfutil@tmpT{TD("\pgfutil@tmpa")}%
\ifcase\c@pgf@counta
\pgfmathsetmacro\pgfutil@tmpA{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpB{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpC{TD("\pgfutil@tmpa")}%
\fi
\advance\c@pgf@counta by1\relax
\ifnum\c@pgf@counta=1\relax
\edef\pgfutil@tmpl{(\pgfutil@tmpT)}%
\else
\edef\pgfutil@tmpl{\pgfutil@tmpl -- (\pgfutil@tmpT)}%
\fi
}%
\ifnum\c@pgf@counta<3\relax
\typeout{A face needs at least three vertices. However, only \the\c@pgf@counta\space vertices were specified.}%
\else
\edef\pgfutil@tmpO{\pgfkeysvalueof{/tikz/3d/polyhedron/O}}%
\pgfmathsetmacro\pgfutil@tmpO{TD("\pgfutil@tmpO")}%
\edef\pgfutil@tmpL{\pgfkeysvalueof{/tikz/3d/polyhedron/L}}%
\pgfmathsetmacro\pgfutil@tmpL{TD("\pgfutil@tmpL")}%
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpC)-(\pgfutil@tmpA)")}%
\pgfmathsetmacro{\pgfutil@tmpc}{TD("(\pgfutil@tmpA)-(\pgfutil@tmpO)")}%
\pgfmathtruncatemacro{\pgfutil@tmpd}{sign(TD("(\pgfutil@tmpb)o(\pgfutil@tmpc)"))}%
\ifnum\pgfutil@tmpd=-1\relax
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpA)-(\pgfutil@tmpC)")}%
\fi
\pgfmathsetmacro{\pgfutil@tmpe}{screendepth(\pgfutil@tmpb)}%
\pgfmathsetmacro{\pgfutil@tmpf}{sqrt(TD("(\pgfutil@tmpb)o(\pgfutil@tmpb)"))}%
\pgfmathsetmacro{\pgfutil@tmpg}{sqrt(TD("(\pgfutil@tmpL)o(\pgfutil@tmpL)"))}%
\pgfmathsetmacro{\pgfutil@tmph}{TD("(\pgfutil@tmpL)o(\pgfutil@tmpb)")/\pgfutil@tmpf/\pgfutil@tmpg}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{70+30*\pgfutil@tmph}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{\pgfkeysvalueof{/tikz/3d/polyhedron/shading function}(\pgfutil@tmph)}%
\ifdim\pgfutil@tmpe pt<0pt\relax
\scoped[on background layer]{%
\draw[fill=tikz@td@face@color!\pgfutil@tmpi!black,3d/polyhedron/back] \pgfutil@tmpl -- cycle;}
\else
\draw[fill=tikz@td@face@color!\pgfutil@tmpi!black,3d/polyhedron/fore] \pgfutil@tmpl -- cycle;
\fi
\fi
\endgroup
},
color/.code={\colorlet{tikz@td@face@color}{#1}},color=yellow,
O/.initial={(0,0,0)},% point inside the polyhedron
L/.initial={(1,1,1)},% "light source",
fore/.style={draw,solid},
back/.style={draw,dashed,fill=none},
shading function/.initial={tikztdpolyhedronshade},
/tikz/declare function={tikztdpolyhedronshade(\x)=70+30*\x;}
}%
% temporary
% conceivably a more developed version will go into 3dtools
\tikzset{pics/generic tetrahedron/.style={code={\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\ifcase\c@pgf@counta
\edef\pgfutil@tmpA{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpB{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpC{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpD{\pgfutil@tmpa}%
\fi
\advance\c@pgf@counta by1\relax
}%
% \typeout{A=\pgfutil@tmpA,B=\pgfutil@tmpB,C=\pgfutil@tmpC,D=\pgfutil@tmpD}
\ifnum\c@pgf@counta=4\relax
\tikzset{3d/polyhedron/.cd,
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpC}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpC},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpB},{\pgfutil@tmpC},{\pgfutil@tmpD}}
}
\else
\typeout{A tetrahedron needs 4 vertices. However, you specified \the\c@pgf@counta\space vertices.}%
\fi
}}}
\makeatother
\begin{document}
\foreach\Angle in {5,15,...,355}
{\begin{tikzpicture}[dot/.style={circle,inner sep=1pt,fill},
declare function={a=3;l1=a;l2=a*sqrt(3);l3=2*a;l4=a*sqrt(2);l5=a;l6=a*sqrt(5);}]
% ^^^ the lengths of the tetrahedron
\begin{scope}[3d/install view={phi=\Angle,psi=0,theta=70}]
% construct a triangle of three vertices in the xy plane
% using the cosine law
\pgfmathsetmacro{\mytheta}{acos((l3*l3-l1*l1-l2*l2)/(2*l1*l2))}
\path (0,0,0) coordinate (v1)
(l1,0,0) coordinate (v2)
({l2*cos(\mytheta)},{l2*sin(\mytheta)},0) coordinate (v3);
% we do not need this here but in principle 3dtools is prepared to
% deal with arbitrarily oriented tetrahedra.
% \path[overlay,3d/define orthonormal dreibein={A={(v1)},B={(v2)},C={(v3)}}];
% however, the following works for the above input
% this is a dictionary for the code at https://stackoverflow.com/a/18654302
\tikzset{declare function={d=l1;i=l2*cos(\mytheta);j=l2*sin(\mytheta);
r1=l4;r2=l5;r3=l6;}}
\pgfmathsetmacro{\myx}{(r1*r1-r2*r2+d*d)/(2*d)}
\pgfmathsetmacro{\myy}{(r1*r1-r3*r3+2*i*\myx+j*j)/(2*j)}
\pgfmathsetmacro{\tmp}{r1*r1-\myx*\myx-\myy*\myy}
\ifdim\tmp pt<0pt
\typeout{Spheres do not intersect.}
\else
\pgfmathsetmacro{\myz}{sqrt(\tmp)}
\path (\myx,\myy,\myz) coordinate (v4);
% an educated guess for a coordinate inside the polyhedron
% \path[3d/plane through={(v1) and (v2) and (v3) named pABC}];
% \path[3d/project={(v4) on pABC}] coordinate (v4');
\path[overlay,3d coordinate={(O')=0.25*(v1)+0.25*(v2)+0.25*(v3)+0.1*(v4)}];
\path[3d/polyhedron/O={(O')},3d/polyhedron/fore/.append style={opacity=0.7}]
pic[transform shape]{%
generic tetrahedron={{(v1)},{(v2)},{(v3)},{(v4)}}};
\path[3d/circumsphere center={A={(v1)},B={(v2)},C={(v3)},D={(v4)}}]
coordinate (I);
\path[3d/intersection of three spheres={A={(v1)},B={(v2)},C={(v3)},
rA=l4,rB=l5,rC=l6}];
\pgfmathsetmacro{\myv}{TD("(v4)")}
\pgfmathsetmacro{\myIa}{TD("(i1)")}
\pgfmathsetmacro{\myIb}{TD("(i2)")}
\pgfmathsetmacro{\myex}{TD("(ex)")}
\pgfmathsetmacro{\myey}{TD("(ey)")}
\pgfmathsetmacro{\myez}{TD("(ez)")}
% \typeout{(ex)=(\myex),(ey)=(\myey),(ez)=(\myez)}
% \typeout{(v4)=(\myv),(i1)=(\myIa),(i2)=(\myIb)}
\fi
\end{scope}
\pgfmathsetmacro{\dAB}{sqrt(TD("(v1)-(v2)o(v1)-(v2)"))}
\pgfmathsetmacro{\dAC}{sqrt(TD("(v1)-(v3)o(v1)-(v3)"))}
\pgfmathsetmacro{\dAD}{sqrt(TD("(v1)-(v4)o(v1)-(v4)"))}
\pgfmathsetmacro{\dBC}{sqrt(TD("(v2)-(v3)o(v2)-(v3)"))}
\pgfmathsetmacro{\dBD}{sqrt(TD("(v2)-(v4)o(v2)-(v4)"))}
\pgfmathsetmacro{\dCD}{sqrt(TD("(v3)-(v4)o(v3)-(v4)"))}
\pgfmathsetmacro{\lA}{l1}
\pgfmathsetmacro{\lB}{l2}
\pgfmathsetmacro{\lC}{l3}
\pgfmathsetmacro{\lD}{l4}
\pgfmathsetmacro{\lE}{l5}
\pgfmathsetmacro{\lF}{l6}
% check the lengths of the edges
%\typeout{(\dAB,\dAC,\dBC,\dAD,\dBD,\dCD) vs. (\lA,\lB,\lC,\lD,\lE,\lF)}
\pgfmathsetmacro{\csr}{sqrt(TD("(v1)-(I)o(v1)-(I)"))}
% check radius
% \foreach \XX in {1,...,4}
% {\pgfmathsetmacro{\csr}{sqrt(TD("(v\XX)-(I)o(v\XX)-(I)"))}
% % \pgfmathsetmacro{\myd}{TD("(v\XX)-(I)"))}
% % \pgfmathsetmacro{\csr}{sqrt(TD("(\myd)o(\myd)"))}
% \typeout{\csr}}
\draw[ball color=gray,fill opacity=0.2] (I) circle[radius=\csr];
% \path foreach \X in {1,...,4}
% {(v\X) coordinate[dot,label=above:{$v_\X$}]}
% (I) (I) coordinate[dot,label=above:{$I=\pgfmathparse{TD("(I)")}%
% (\pgfmathprintvector\pgfmathresult)^T$}];
\end{tikzpicture}}
\end{document}
```
This version uses the new key `intersection of three spheres` that was added to `3dtools`.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\usetikzlibrary{backgrounds}
\makeatletter
% something like this may go into the 3dtools library
\tikzset{3d/.cd,polyhedron/.cd,
draw face with corners/.code={\begingroup\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\pgfmathsetmacro\pgfutil@tmpT{TD("\pgfutil@tmpa")}%
\ifcase\c@pgf@counta
\pgfmathsetmacro\pgfutil@tmpA{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpB{TD("\pgfutil@tmpa")}%
\or
\pgfmathsetmacro\pgfutil@tmpC{TD("\pgfutil@tmpa")}%
\fi
\advance\c@pgf@counta by1\relax
\ifnum\c@pgf@counta=1\relax
\edef\pgfutil@tmpl{(\pgfutil@tmpT)}%
\else
\edef\pgfutil@tmpl{\pgfutil@tmpl -- (\pgfutil@tmpT)}%
\fi
}%
\ifnum\c@pgf@counta<3\relax
\typeout{A face needs at least three vertices. However, only \the\c@pgf@counta\space vertices were specified.}%
\else
\edef\pgfutil@tmpO{\pgfkeysvalueof{/tikz/3d/polyhedron/O}}%
\pgfmathsetmacro\pgfutil@tmpO{TD("\pgfutil@tmpO")}%
\edef\pgfutil@tmpL{\pgfkeysvalueof{/tikz/3d/polyhedron/L}}%
\pgfmathsetmacro\pgfutil@tmpL{TD("\pgfutil@tmpL")}%
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpC)-(\pgfutil@tmpA)")}%
\pgfmathsetmacro{\pgfutil@tmpc}{TD("(\pgfutil@tmpA)-(\pgfutil@tmpO)")}%
\pgfmathtruncatemacro{\pgfutil@tmpd}{sign(TD("(\pgfutil@tmpb)o(\pgfutil@tmpc)"))}%
\ifnum\pgfutil@tmpd=-1\relax
\pgfmathsetmacro{\pgfutil@tmpb}{TD("(\pgfutil@tmpB)-(\pgfutil@tmpA)x(\pgfutil@tmpA)-(\pgfutil@tmpC)")}%
\fi
\pgfmathsetmacro{\pgfutil@tmpe}{screendepth(\pgfutil@tmpb)}%
\pgfmathsetmacro{\pgfutil@tmpf}{sqrt(TD("(\pgfutil@tmpb)o(\pgfutil@tmpb)"))}%
\pgfmathsetmacro{\pgfutil@tmpg}{sqrt(TD("(\pgfutil@tmpL)o(\pgfutil@tmpL)"))}%
\pgfmathsetmacro{\pgfutil@tmph}{TD("(\pgfutil@tmpL)o(\pgfutil@tmpb)")/\pgfutil@tmpf/\pgfutil@tmpg}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{70+30*\pgfutil@tmph}%
\pgfmathtruncatemacro{\pgfutil@tmpi}{\pgfkeysvalueof{/tikz/3d/polyhedron/shading function}(\pgfutil@tmph)}%
\ifdim\pgfutil@tmpe pt<0pt\relax
\scoped[on background layer]{%
\draw[fill=tikz@td@face@color!\pgfutil@tmpi!black,3d/polyhedron/back] \pgfutil@tmpl -- cycle;}
\else
\draw[fill=tikz@td@face@color!\pgfutil@tmpi!black,3d/polyhedron/fore] \pgfutil@tmpl -- cycle;
\fi
\fi
\endgroup
},
color/.code={\colorlet{tikz@td@face@color}{#1}},color=yellow,
O/.initial={(0,0,0)},% point inside the polyhedron
L/.initial={(1,1,1)},% "light source",
fore/.style={draw,solid},
back/.style={draw,dashed,fill=none},
shading function/.initial={tikztdpolyhedronshade},
/tikz/declare function={tikztdpolyhedronshade(\x)=70+30*\x;}
}%
% temporary
% conceivably a more developed version will go into 3dtools
\tikzset{pics/generic tetrahedron/.style={code={\c@pgf@counta0\relax
\pgfutil@for\pgfutil@tmpa:={#1}\do{%
\ifcase\c@pgf@counta
\edef\pgfutil@tmpA{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpB{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpC{\pgfutil@tmpa}%
\or
\edef\pgfutil@tmpD{\pgfutil@tmpa}%
\fi
\advance\c@pgf@counta by1\relax
}%
%\typeout{A=\pgfutil@tmpA,B=\pgfutil@tmpB,C=\pgfutil@tmpC,D=\pgfutil@tmpD}
\ifnum\c@pgf@counta=4\relax
\tikzset{3d/polyhedron/.cd,
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpC}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpB},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpA},{\pgfutil@tmpC},{\pgfutil@tmpD}},
draw face with corners={{\pgfutil@tmpB},{\pgfutil@tmpC},{\pgfutil@tmpD}}
}
\else
\typeout{A tetrahedron needs 4 vertices. However, you specified \the\c@pgf@counta\space vertices.}%
\fi
}}}
\makeatother
\begin{document}
\foreach\Angle in {155} %{5,15,...,355}
{\begin{tikzpicture}[dot/.style={circle,inner sep=1pt,fill},
declare function={a=3;l12=a;l23=a*sqrt(3);l13=2*a;
l14=a*sqrt(2);l24=a;l34=a*sqrt(5);}]
% ^^^ the lengths of the tetrahedron;
% l12 is the distance between vertex 1 and vertex 2, etc.
\begin{scope}[3d/install view={phi=\Angle,psi=0,theta=70}]
\pgfmathsetmacro{\mytheta}{acos((l23*l23-l12*l12-l13*l13)/(2*l12*l13))}
\pgfmathtruncatemacro{\itest}{(cos(\mytheta)<0)}
\ifnum\itest=1
\pgfmathsetmacro{\mytheta}{180-\mytheta}
\fi
\path (0,0,0) coordinate (v1) (0,0,l12) coordinate (v2)
({l13*sin(\mytheta)},0,{l13*cos(\mytheta)}) coordinate (v3);
\pgfmathtruncatemacro{\itest}{(l14+l24>l12)&&(l14+l34>l13)&&(l24+l34>l23)}
\ifnum\itest<1
\typeout{Not all of the spheres do intersect.}
\else
\path[3d/intersection of three spheres={A={(v1)},B={(v2)},C={(v3)},
rA=l14,rB=l24,rC=l34}];
\pgfmathsetmacro{\myIa}{TD("(i1)")}
\path (\myIa) coordinate (v4);
% an educated guess for a coordinate inside the polyhedron
\path[overlay,3d coordinate={(O')=0.25*(v1)+0.25*(v2)+0.25*(v3)+0.1*(v4)}];
\path[3d/polyhedron/O={(O')},3d/polyhedron/fore/.append style={opacity=0.7}]
pic[transform shape]{%
generic tetrahedron={{(v1)},{(v2)},{(v3)},{(v4)}}};
\path[3d/circumsphere center={A={(v1)},B={(v2)},C={(v3)},D={(v4)}}]
coordinate (I);
\fi
\end{scope}
\pgfmathsetmacro{\csr}{sqrt(TD("(v1)-(I)o(v1)-(I)"))}
\draw[ball color=gray,fill opacity=0.2] (I) circle[radius=\csr];
\end{tikzpicture}}
\end{document}
```