How to draw this picture with a nice view? - TeX

TopAnswers TeX

Top Answer

user 3.14159

The depicted projection is not orthographic. I copy the proof from [here](https://tex.stackexchange.com/a/448048).
```
\documentclass[fleqn]{article}
\usepackage{amsmath,marvosym}
\begin{document}
You wish to have a coordinate system that 
\begin{enumerate}
 \item preserves shapes and\label{preserve}
 \item has $\vec e_y$ point east, $\vec e_z$ point north and $\vec e_x$ point
 south west.\label{directions}
\end{enumerate}
The first requirement means that the coordinate axes are orthogonal,
\begin{equation}\label{eq:orthogonality}
 \vec e_x\cdot \vec e_y~=~\vec e_x\cdot \vec e_z~=~\vec e_y\cdot \vec e_z
~=~0\;.
\end{equation}
So we wish to find a two--dimensional projection of these vectors that fulfill
the requirement \ref{directions}. Decompose the vectors in two--dimensional
projections on the paper plane $\vec e_i^{(\|)}$ and the orthogonal complements
$\vec e_i^{(\perp)}$. Clearly, the $\vec e_i^{(\perp)}$ are just
one--dimensional objects, which we will just call $e_i^{(\perp)}$. Requirement \ref{directions} implies that
\begin{equation}
 \vec e_x^{(\|)} \cdot \vec e_y^{(\|)}=
\vec e_x^{(\|)} \cdot \vec e_z^{(\|)}=:\xi\ne0\;.
\end{equation}
Due to the orthogonality relations \eqref{eq:orthogonality}, this means that
\begin{equation}
 e_x^{(\perp)} \cdot e_y^{(\perp)}=
 e_x^{(\perp)} \cdot e_z^{(\perp)}=-\xi~\ne~0\;.
\end{equation}
None of the $e_i^{(\perp)}$ may vanish as otherwise there won't be an $x$--axis,
and
\begin{equation}
e_y^{(\perp)}=e_z^{(\perp)}=-\frac{\xi}{e_x^{(\perp)}}\;. 
\end{equation}
However, requirement \ref{directions} 
implies that $\vec e_y^{(\|)} \cdot \vec e_z^{(\|)}=0$, so
\begin{equation}
 \vec e_y\cdot \vec e_z=\vec e_y^{(\|)} \cdot \vec e_z^{(\|)}
 +e_y^{(\perp)} \cdot e_z^{(\perp)}=0+\left(\frac{\xi}{e_x^{(\perp)}}\right)^2
 ~\ne~0\;.\qquad \text{\Huge\Lightning}
\end{equation}
\end{document}
```
![Screen Shot 2020-09-15 at 9.50.10 PM.png](/image?hash=549ea65e779927ac4a62685b8a330fa85da50f0e75aafc256e3ae13f53baaf29)

So we need to install a non-orthographic view, so we won't need `tikz-3dplot`. Here is an example. We just define `(ex)` to point to the right, `(ez)` to point up, and take some `(ey)` vector, which can be changed to get a different/better/nicer result. 
```
\documentclass[12pt,tikz,border = 3mm]{standalone}
\usetikzlibrary{3d}
\begin{document}
\begin{tikzpicture}[scale=1,declare function={a=5;}]
 \path (1,0) coordinate (ex) (40:0.7) coordinate (ey) (0,1) coordinate (ez);
 \begin{scope}[x={(ex)},y={(ey)},z={(ez)},transform shape,
 	pics/.cd,squares/.style={code={
	 \draw (-a,-a) rectangle (a,a)
	  (-a/3,-a/3) rectangle (a/3,a/3);
	}}]
  \path[canvas is xy plane at z=a] pic{squares};
  \path[canvas is xz plane at y=-a] pic{squares};
  \path[canvas is yz plane at x=a] pic{squares};
 \end{scope}
\end{tikzpicture}
\end{document} 
```
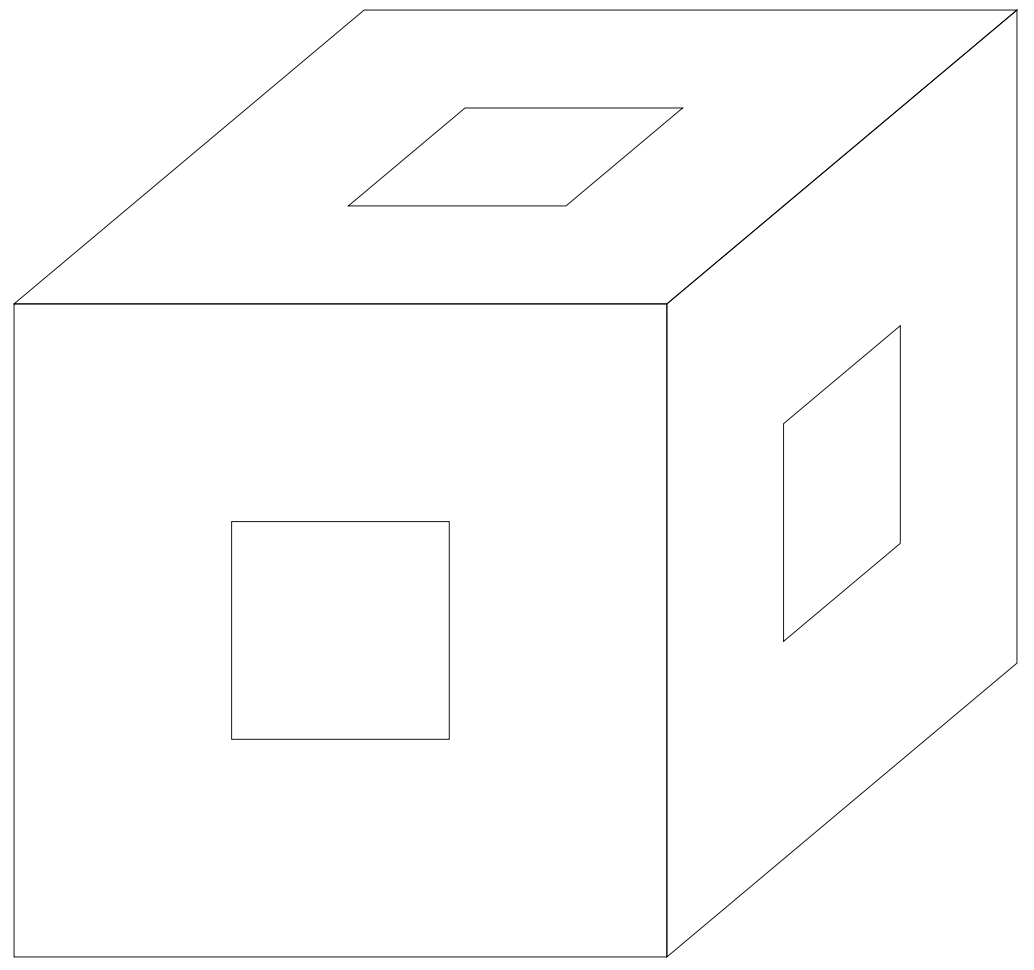
![Screen Shot 2020-09-15 at 9.58.07 PM.png](/image?hash=3ef1b2d14bb6c9d53399ab62d54a6293c6eb5ef3f27006ca3d5f590ddcbdad8a)

If you have repetive tasks, you can use `pic`s in which you only change the basis vectors.
```
\documentclass[12pt,tikz,border = 3mm]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}[scale=1,declare function={a=5;b=0;}]
 \path (1,0) coordinate (ex) (40:0.7) coordinate (ey) (0,1) coordinate (ez);
 \begin{scope}[transform shape,pics/.cd,side/.style={code={\ifcase#1
	 \edef\mycs{x={(ex)},y={(ey)},z={(ez)}}
	\or 
	 \edef\mycs{x={(ey)},y={(ez)},z={(ex)}}
	\or 
	 \edef\mycs{x={(ez)},y={(ex)},z={($-1*(ey)$)}}
	\fi
	\begin{scope}[style/.expanded=\mycs]
	 \draw
	  (-a,-a,a) -- (a,-a,a) -- (a,a,a) -- (-a,a,a) -- cycle
	  (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle;
	 \clip (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle;
	 \draw[fill=gray!10] (-a/3,-a/3,a) -- (a/3,-a/3,a)
	  -- (a/3,-a/3,b) -- (-a/3,-a/3,b) -- cycle;
	 \draw[fill=gray!20] (-a/3,-a/3,a) -- (-a/3,a/3,a)
	  -- (-a/3,a/3,b) -- (-a/3,-a/3,b) -- cycle;
	 \draw[fill=gray!30] (-a/3,a/3,a) -- (a/3,a/3,a)
	  -- (a/3,a/3,b) -- (-a/3,a/3,b) -- cycle;
	 \draw[fill=gray!40] (a/3,a/3,a) -- (a/3,-a/3,a)
	  -- (a/3,-a/3,b) -- (a/3,a/3,b) -- cycle;
	\end{scope}  
	}}]
	\path pic{side=0};
	\path pic{side=1};
	\path pic{side=2};
 \end{scope}
\end{tikzpicture}
\end{document}
```
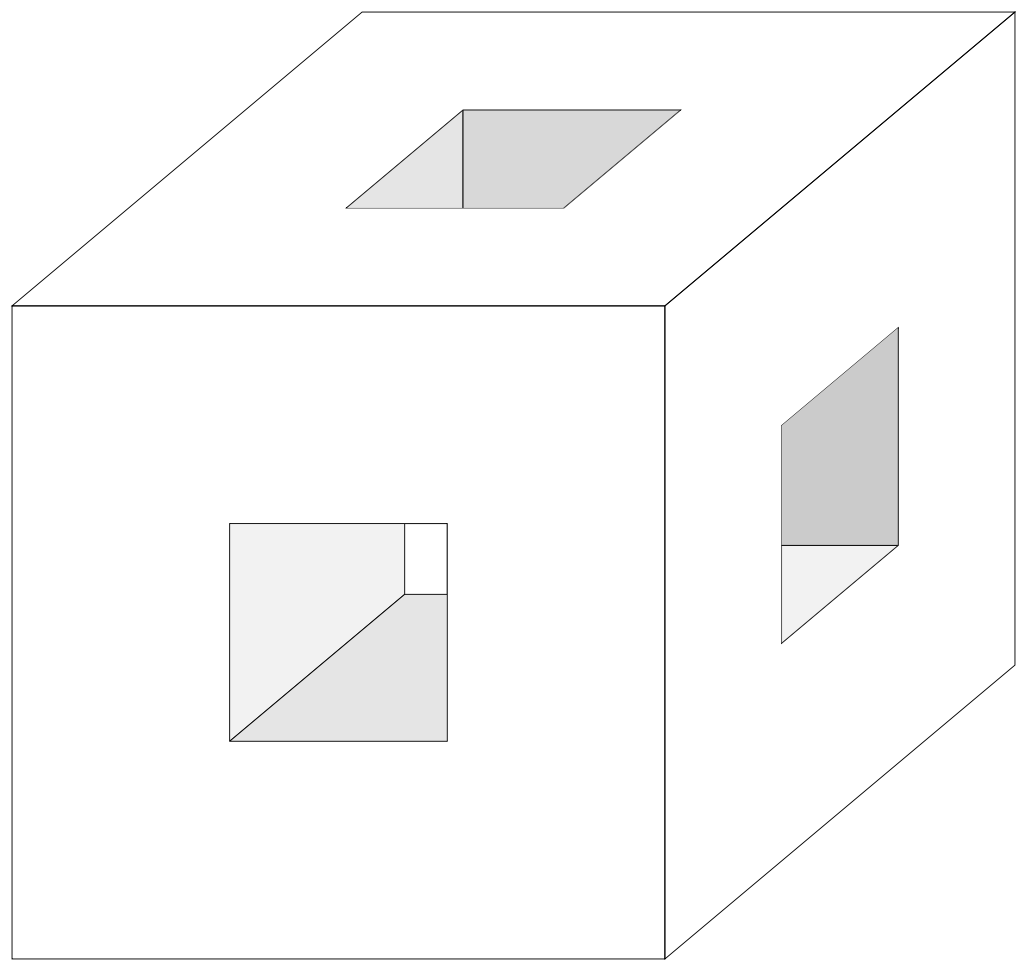
![Screen Shot 2020-09-15 at 10.34.07 PM.png](/image?hash=d32a540eaf88d613f9d85dc6ef86fcc3f5fc93b7e5d13dee50c4a430ea1fc0df)

Of course, if you use nonorthographic projections, you cannot change the view angles simply because there are no well defined view angles.

However, it is of course possible to do the same things with an orthographic view. Then all one has do is to flip some signs depending on the view angle, or the screen depth of the basis vectors.
```
\documentclass[12pt,tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\begin{document}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{70}{\Angle} 
\begin{tikzpicture}[tdplot_main_coords,scale=1,declare function={a=5;b=0;}]
 \path (1,0,0) coordinate (ex) (0,1,0) coordinate (ey) (0,0,1) coordinate (ez);
 \path[tdplot_screen_coords,use as bounding box] (-1.5*a,-1.5*a) rectangle (1.5*a,1.5*a);
 \begin{scope}[transform shape,pics/.cd,side/.style={code={\ifcase##1
     \pgfmathsetmacro{\iflip}{sign(screendepth(0,0,1))}
	 \edef\mycs{x={(ex)},y={(ey)},z={($\iflip*(ez)$)}}
	\or 
     \pgfmathsetmacro{\iflip}{sign(screendepth(1,0,0))}
	 \edef\mycs{x={(ey)},y={(ez)},z={($\iflip*(ex)$)}}
	\or 
     \pgfmathsetmacro{\iflip}{sign(screendepth(0,1,0))}
	 \edef\mycs{x={(ez)},y={(ex)},z={($\iflip*(ey)$)}}
	\fi
	\begin{scope}[style/.expanded=\mycs]
	 \draw
	  (-a,-a,a) -- (a,-a,a) -- (a,a,a) -- (-a,a,a) -- cycle
	  (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle;
	 \clip (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle;
	 \draw[fill=gray!10] (-a/3,-a/3,a) -- (a/3,-a/3,a)
	  -- (a/3,-a/3,b) -- (-a/3,-a/3,b) -- cycle;
	 \draw[fill=gray!20] (-a/3,-a/3,a) -- (-a/3,a/3,a)
	  -- (-a/3,a/3,b) -- (-a/3,-a/3,b) -- cycle;
	 \draw[fill=gray!30] (-a/3,a/3,a) -- (a/3,a/3,a)
	  -- (a/3,a/3,b) -- (-a/3,a/3,b) -- cycle;
	 \draw[fill=gray!40] (a/3,a/3,a) -- (a/3,-a/3,a)
	  -- (a/3,-a/3,b) -- (a/3,a/3,b) -- cycle;
	\end{scope}  
	}}]
	\path pic{side=0};
	\path pic{side=1};
	\path pic{side=2};
 \end{scope}
\end{tikzpicture}}
\end{document} 
```
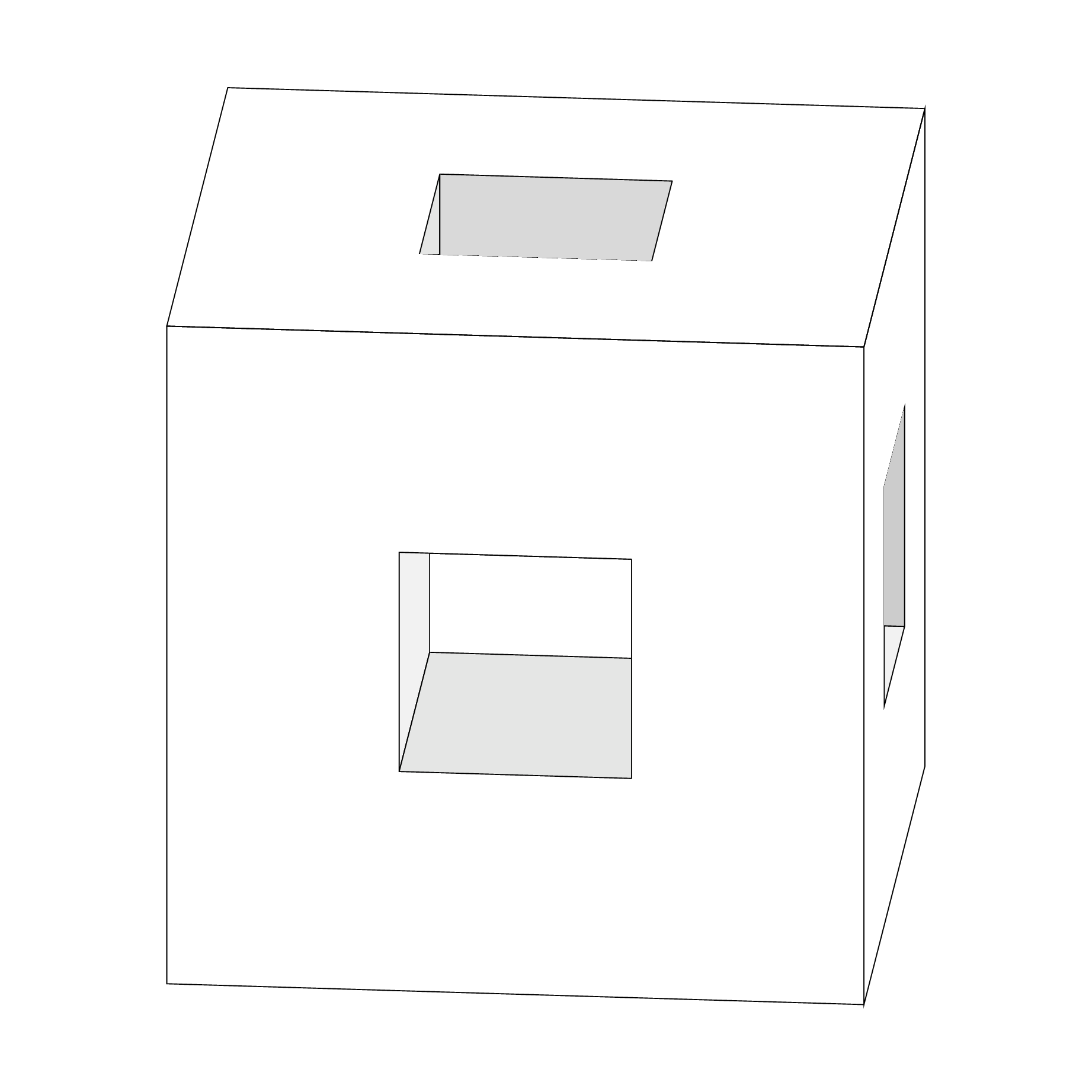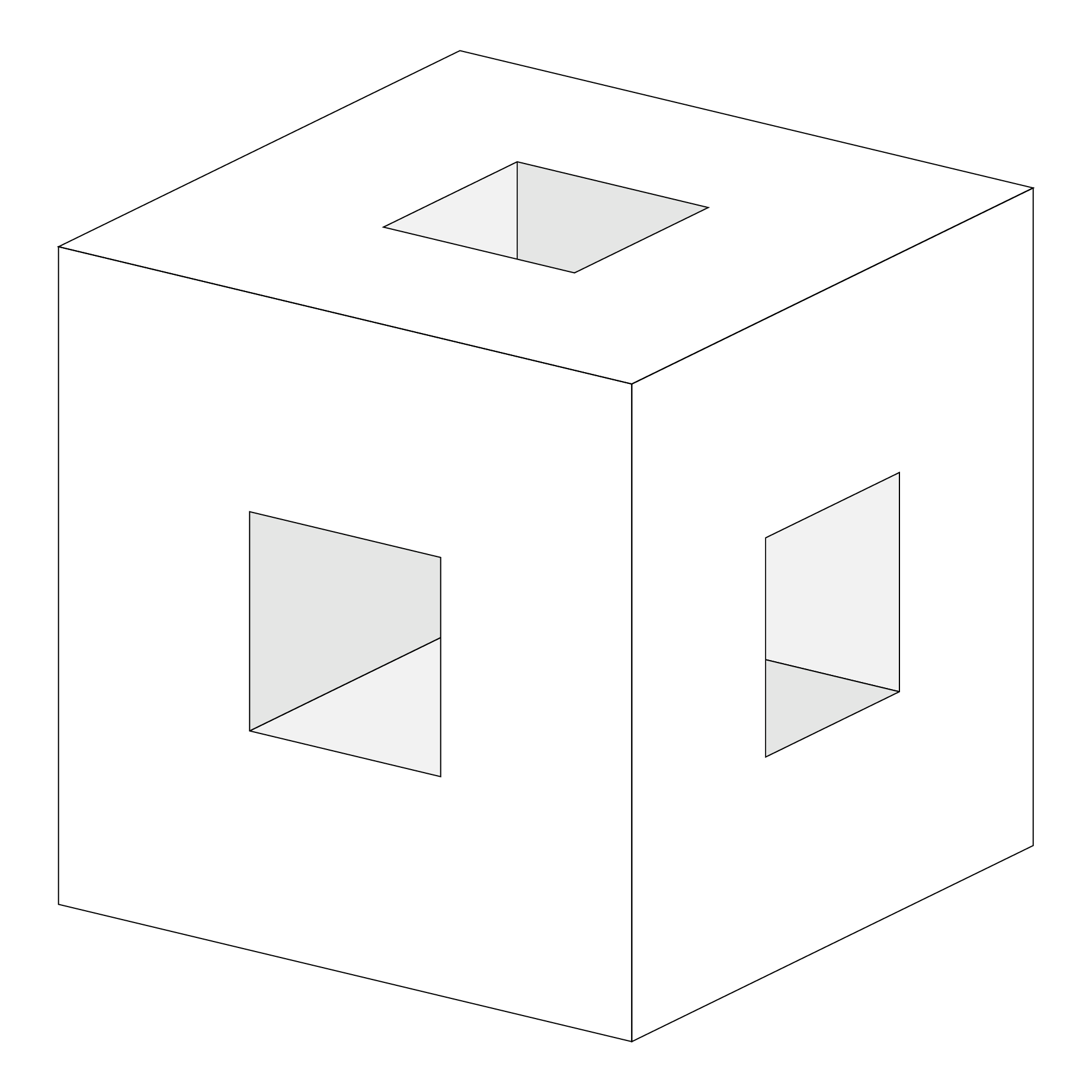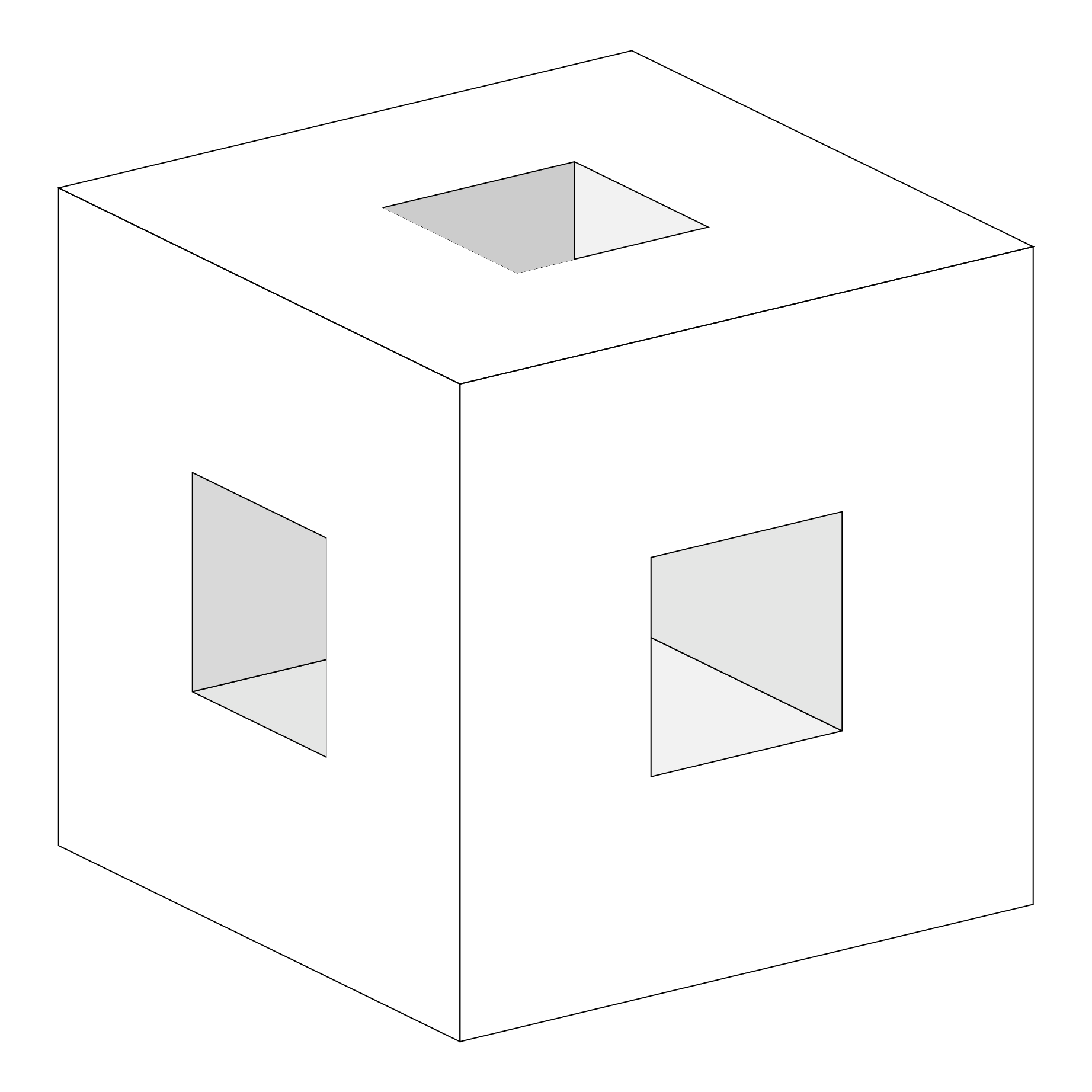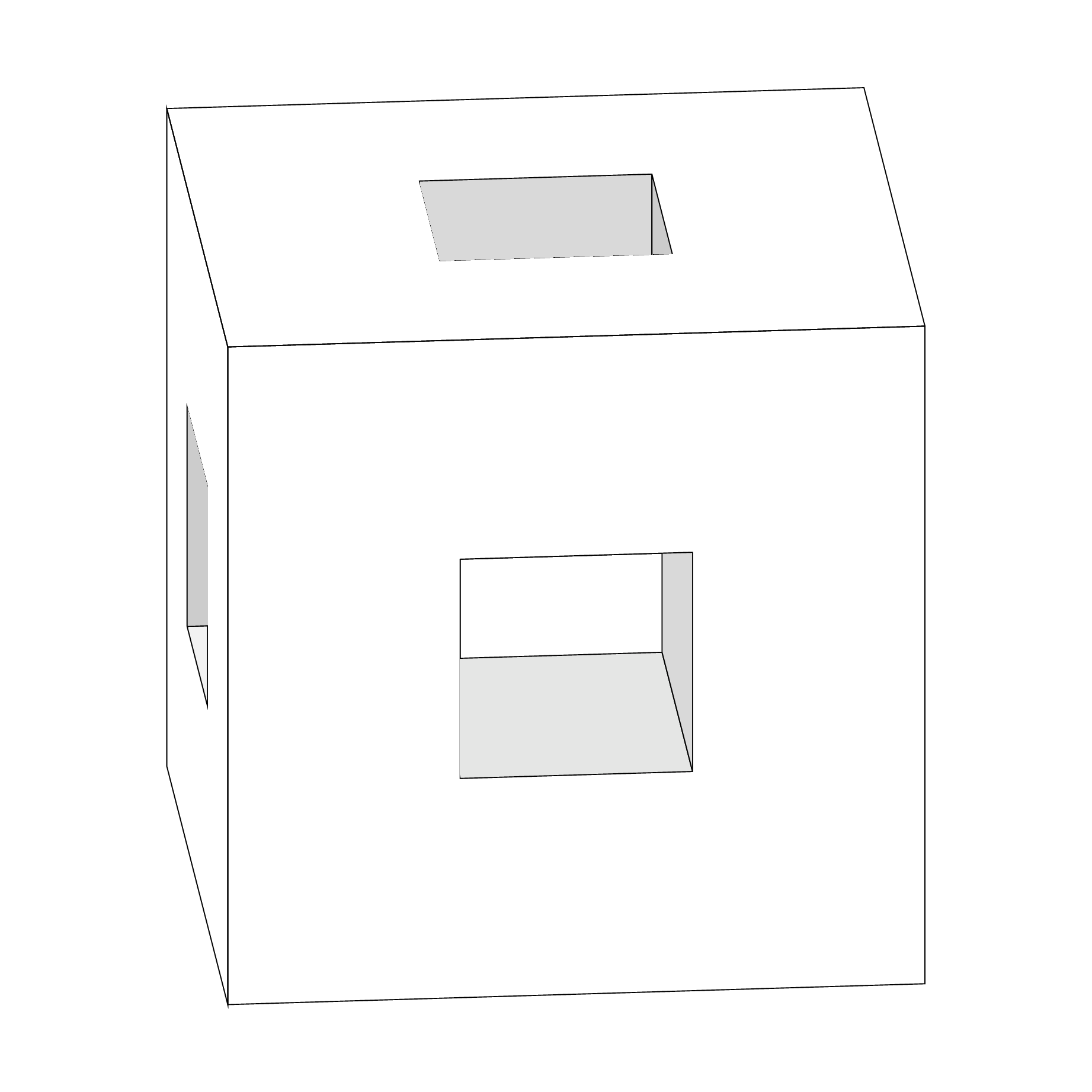
![ani.gif](/image?hash=43874df2105a01c3f86b8f2175725e024ae90a088415e229a9e21a989f0a6212)

Note that this draws only three faces, so if you want to have a real "look inside" feel this will require more efforts.

@marmot, re: [your answer](#a1575), For a long time, You asked about `cut` commnad in Asympote. Now I see it at here [Asymptote - Figure 0047](http://asy.marris.fr/asymptote/Solides/index.html?fbclid=IwAR3bTKIghQoKaZUVWtACr5sByDBxXGrxc_EDQFmg7ggk4hE8fxTFQ-mfCA8). You can see it ``` import three; size(7cm); currentprojection=orthographic(5,4,3); triple pA=(2,2,0), pB=(-2,2,0), pC=(-2,-2,0), pD=(2,-2,0), pS=(0,0,5); path3 cercle = pA..pB..pC..pD..cycle; draw(pS--pD--pA--pS--pB--pA); draw(pD--pC--pS^^pC--pB,dashed); // Pas facile de détecter la partie cachée du cercle ! path pvisib1 = cut(project(cercle),project(pB--pS--pD),1).before, pvisib2 = cut(project(cercle),project(pB--pS--pD),2).after, pcache = cut(cut(project(cercle),project(pB--pS--pD),1).after,project(pB--pS--pD),1).before; draw(invert(pvisib1,Z,O)^^invert(pvisib2,Z,O),blue); draw(invert(pcache,Z,O),red+dashed); // --- pour des explications sur cut : voir la sous-galerie "Intersections". label("$A$",pA,S); label("$B$",pB,E); label("$C$",pC,NW); label("$D$",pD,W); label("$S$",pS,N); ```

Yes. I just want to draw a stack of cubes. Problem 7. Seven cubes, whose volumes are $1$, $8$, $27$, $64$, $125$, $216$, and $343$ cubic units, are stacked vertically to form a tower in which the volumes of the cubes decrease from bottom to top. Except for the bottom cube, the bottom face of each cube lies completely on top of the cube below it. What is the total surface area of the tower (including the bottom) in square units?

If you want to draw one picture, yes. If you want to prepare some notes with several pictures, you may want to pay some attention that they look similar. For instance, the arrow heads should look the same, the font size should be consistent with the surrounding text, and so on. This is my main motivation for using Ti*k*Z and pgfplots, even for 3d. If I embed the codes in a beamer presentation, the font will automatically match, And one can use macros and so on to unify notation. This is particularly important these days when one does remote teaching and needs to prepare notes and slides efficiently.

I do not know if this goes in the right direction. (You also do not `3dtools` here, `tikz-3dplot` also can do these things.) ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools \begin{document} \begin{tikzpicture}[line cap=round,line join=round,scale=0.2, declare function={R=16;h=-7;theta=70;r=sqrt(R*R-h*h);}] \pgfmathsetmacro{\alphacrit}{asin(h/R)} \begin{scope}[3d/install view={phi=0,theta=theta}] \pgfmathsetmacro{\betacrit}{asin(h*cot(theta)/R)} \typeout{\alphacrit,\betacrit} \begin{scope} \clip plot[smooth,domain=\betacrit:-180-\betacrit,variable=\t] ({r*cos(\t)},{r*sin(\t)},h) [3d/screen coords] -- plot[smooth,domain=-180-\alphacrit:\alphacrit,variable=\t] ({R*cos(\t)},{R*sin(\t)}); \shade[3d/screen coords,ball color=blue!30] (0,0) circle[radius=R]; \end{scope} \end{scope} \begin{scope}[3d/install view={phi=20,theta=theta}, declare function={jump(\t)=(abs(sin(\t))<0.15?1:0);}] \draw[blue!60,dashed] plot[smooth,domain=180-\alphacrit-8:\alphacrit+8,variable=\t] ({(R+0.1*r)*cos(\t)},0,{(R+0.1*r)*sin(\t)}); \draw[inner color=gray!40,outer color=gray!10] plot[domain=0:360,samples=181,variable=\t] ({r*(1+0.1*jump(\t))*cos(\t)},{r*(1+0.1*jump(\t))*sin(\t)},{h+jump(\t)}); \end{scope} \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1575), A question has no an answer is how to draw like this picture ![ScreenHunter 1053.png](/image?hash=91c2e93f0a7a953e191bcc92cfe03e533a09b814937aa0a996aebb9a4d2e4bdc) A code that tried ``` \documentclass{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.17} \usepackage{tikz} \begin{document} \begin{tikzpicture}[scale=1.3] \begin{axis} [hide axis,axis equal, view={115}{28},xmax=24, ymax=24, zmax=24] \addplot3[domain=0:2*pi, dashed, samples=50, samples y=0, no marks, smooth, blue]({0},{16*cos(deg(x))},{16*sin(deg(x))}); \addplot3[surf, colormap= {cyangray}{color=(cyan) color=(cyan)},domain=29*pi/45:pi,y domain=0:2*pi,samples = 11, samples y=64,z buffer = sort,] ({16*sin(deg(x))*cos(deg(y))},{16*sin(deg(x))*sin(deg(y))},{16*cos(deg(x))}); \addplot3[domain=0:2*pi, samples=51, samples y=0, no marks, smooth]({sqrt(207)*cos(deg(x))},{sqrt(207)*sin(deg(x))},{-7}); \draw[-stealth] (0,-19,0)--(0,23,0)node[right]{\tiny $y$ (cm)}; \draw[-stealth] (0,0,-22)--(0,0,24)node[above]{\tiny $z$ (cm)}; \draw (0,0,-7)--(0,2,-7) (0,15.5,-7)--(0,24,-7) (0,0,-16) --(0,2,-16) (0,7,-16)--(0,24,-16) (3,0,-16)--(10,0,-16); \draw[<->] (0,17,-15.5)--(0,17,-7.5); \draw[red] (0,0,-7)--(14,0,-7); \draw (0,7,16)node[right]{\tiny $x^2+y^2=16^2=256$} (0,16,-12)node[right]{\tiny 9 cm} (0,1,2)node[below left]{\tiny $0$} (0,1,-7)node[left]{\tiny $-7$} (10,0,-16)node[below]{\tiny $-16$}; \end{axis} \end{tikzpicture} \end{document} ```

It does worry me though how openly obviously conflicted people can rule. In the real life, at least in academia, things are different. You just cannot be on the hiring committee if your spouse applied for the job, you just cannot be the referee of a paper written by your buddies. In fact, you are excluded from the list of potential grant reviewers if the applicant is based in the same institution, or you had a joint paper with them in the last so-and-so years. In the internet there are no such rules, and in a certain way because stackexchange folks have overdone it even by some very loose standards, this site came into existence.

There is probably not much one can do. The internet seems to be the place in which conflicts of interest are not just common, but seem not to concern the users. In fact, it seems to be the place in which people can push their opinions without limits (which even leads to radicalization, but this is not the concern here). Moderators can moderate competing sites without problem. People can claim to be mathematicians and exploit this to tell others how to typeset differential `d`s even though they do not even know that the differential is an operator, and get away with this because some moderator is their friend. Or even worse, claim that, given two real numbers `a` and `b` with `a\ne b`, there is a third option beyond `a>b` and `a<b`, and because they get certain protection a true mathematician leaves the site. I think we have to learn to live with this. While I totally see how someone can be really excited about `asymptote`, I do not think it should be used to suppress other opinions just because one holds a moderator position. For instance, take [this free text book](http://www.gutenberg.org/ebooks/43006). You can download the LaTeX source. The resulting text looks great, the figures look awful. One may want to recreate them, too. They do require dashed lines and look definitely better with vector graphics. It turns out that for such purposes `asymptote` is not too great. In a certain way, the question which of the two, `asymptote` or `tikz`, is "better" is very much like the question which of the two, a washing machine or a dish washer, is better. There is no universal answer, it depends on the situation. If you want to wash cloths, a washing machine is better, if you want to wash dishes, a dish washer.

@marmot, re: [your answer](#a1575), Black Mild is an admin of https://www.facebook.com/ in Vietnam. He alsway says that TikZ 3D is not real 3D. Asymptote is real 3D. Some time, I want to share your code, but, very people do not want to use `tikz-3dplot`. Therefore, I only introduce https://topanswers.xyz/.

I do not know what a parallel projection is. To the best of my knowledge we are using orthographic projection. They can be thought of as perspective projections in the limit in which the distance from the depicted object is much larger than the dimensions of the object.

Yes, of course. One would have to find out which faces are to be drawn. In this case a sign flip of `(ey)` in the third case is sufficient. ``` \documentclass[12pt,tikz,border = 3mm]{standalone} \usepackage{tikz-3dplot} \begin{document} \tdplotsetmaincoords{70}{120} \begin{tikzpicture}[tdplot_main_coords,scale=1,declare function={a=5;b=0;}] \path (1,0,0) coordinate (ex) (0,1,0) coordinate (ey) (0,0,1) coordinate (ez); \begin{scope}[transform shape,pics/.cd,side/.style={code={\ifcase#1 \edef\mycs{x={(ex)},y={(ey)},z={(ez)}} \or \edef\mycs{x={(ey)},y={(ez)},z={(ex)}} \or \edef\mycs{x={(ez)},y={(ex)},z={(ey)}} \fi \begin{scope}[style/.expanded=\mycs] \draw (-a,-a,a) -- (a,-a,a) -- (a,a,a) -- (-a,a,a) -- cycle (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle; \clip (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle; \draw[fill=gray!10] (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,-a/3,b) -- (-a/3,-a/3,b) -- cycle; \draw[fill=gray!20] (-a/3,-a/3,a) -- (-a/3,a/3,a) -- (-a/3,a/3,b) -- (-a/3,-a/3,b) -- cycle; \draw[fill=gray!30] (-a/3,a/3,a) -- (a/3,a/3,a) -- (a/3,a/3,b) -- (-a/3,a/3,b) -- cycle; \draw[fill=gray!40] (a/3,a/3,a) -- (a/3,-a/3,a) -- (a/3,-a/3,b) -- (a/3,a/3,b) -- cycle; \end{scope} }}] \path pic{side=0}; \path pic{side=1}; \path pic{side=2}; \end{scope} \end{tikzpicture} \end{document} ```

You can use e.g. `tikz-3dplot`. ``` \documentclass[12pt,tikz,border = 3mm]{standalone} \usepackage{tikz-3dplot} \begin{document} \tdplotsetmaincoords{70}{20} \begin{tikzpicture}[tdplot_main_coords,scale=1,declare function={a=5;b=0;}] \path (1,0,0) coordinate (ex) (0,1,0) coordinate (ey) (0,0,1) coordinate (ez); \begin{scope}[transform shape,pics/.cd,side/.style={code={\ifcase#1 \edef\mycs{x={(ex)},y={(ey)},z={(ez)}} \or \edef\mycs{x={(ey)},y={(ez)},z={(ex)}} \or \edef\mycs{x={(ez)},y={(ex)},z={($-1*(ey)$)}} \fi \begin{scope}[style/.expanded=\mycs] \draw (-a,-a,a) -- (a,-a,a) -- (a,a,a) -- (-a,a,a) -- cycle (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle; \clip (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,a/3,a) -- (-a/3,a/3,a) -- cycle; \draw[fill=gray!10] (-a/3,-a/3,a) -- (a/3,-a/3,a) -- (a/3,-a/3,b) -- (-a/3,-a/3,b) -- cycle; \draw[fill=gray!20] (-a/3,-a/3,a) -- (-a/3,a/3,a) -- (-a/3,a/3,b) -- (-a/3,-a/3,b) -- cycle; \draw[fill=gray!30] (-a/3,a/3,a) -- (a/3,a/3,a) -- (a/3,a/3,b) -- (-a/3,a/3,b) -- cycle; \draw[fill=gray!40] (a/3,a/3,a) -- (a/3,-a/3,a) -- (a/3,-a/3,b) -- (a/3,a/3,b) -- cycle; \end{scope} }}] \path pic{side=0}; \path pic{side=1}; \path pic{side=2}; \end{scope} \end{tikzpicture} \end{document} ``` ![Screen Shot 2020-09-16 at 7.33.11 AM.png](/image?hash=76c9014ce41207ef02710cf9e7e301b1b4df58bde56738016aad7ecf16ba851f)

1 Answer