Anonymous 1123

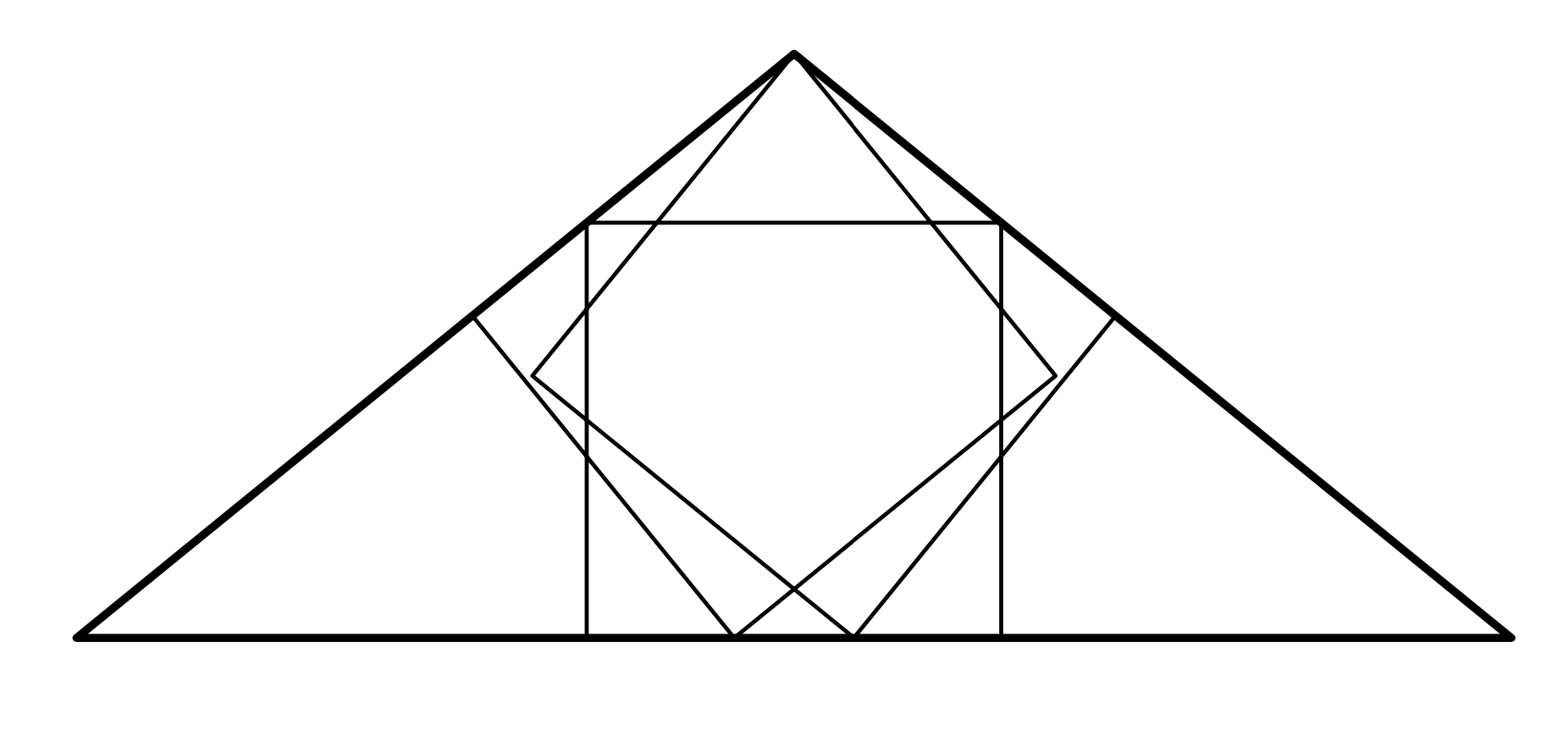
I see Calabi's Triangle at [here](https://mathworld.wolfram.com/CalabisTriangle.html?fbclid=IwAR288tVqTHVQgGwFMScUCt7jKDRPz6PyPSPMnTxkSUwfsNLDytSVsh7hDvE), and this is not my code. I found at [here](https://www.facebook.com/groups/TikZandAsymptote/?epa=SEARCH_BOX)
```
\documentclass[tikz,border=5]{standalone}
\begin{document}
\begin{tikzpicture}[join=round,cap=round]
\def\a{5} \def\b{3} \pgfmathsetmacro\h{sqrt(\b^2-\a^2/4)}
\path (0:0) coordinate (O)
(180:\a/2) coordinate (A)
(0:\a/2) coordinate (B)
(90:\h) coordinate (C)
(0:\h) coordinate (I)
(I)+(C) coordinate (H)
(intersection of A--H and B--C) coordinate (P)
(barycentric cs:P=1,I=1,H=-1)coordinate (PQ)
(intersection of P--PQ and A--B) coordinate (Q)
(barycentric cs:O=-2,Q=1) coordinate (R)
([rotate around={90:(R)}]Q) coordinate (S)
([rotate around={90:(B)}]C)coordinate(J)
(intersection of C--J and A--B) coordinate (M)
(barycentric cs:M=1,B=1,J=-1)coordinate (MN)
(intersection of M--MN and C--B) coordinate(N)
([rotate around={90:(M)}]N)coordinate(L)
([rotate around={-90:(A)}]C)coordinate(K)
(intersection of C--K and A--B) coordinate(Y)
(barycentric cs:Y=1,A=1,K=-1)coordinate (YZ)
(intersection of Y--YZ and C--A) coordinate (Z)
([rotate around={-90:(Y)}]Z)coordinate(X);
\draw[densely dotted,very thin]
(O)--(C)--(H)--(I) (A)--(H)
(C)--(J)--(B)
(C)--(K)--(A);
\draw (A)--(B)--(C)--cycle
(R)--(S)--(P)--(Q)
(C)--(L)--(M)--(N)
(C)--(X)--(Y)--(Z);
\end{tikzpicture}
\end{document}
```
How to draw Calabi's Triangle with another way?
Top Answer
user 3.14159

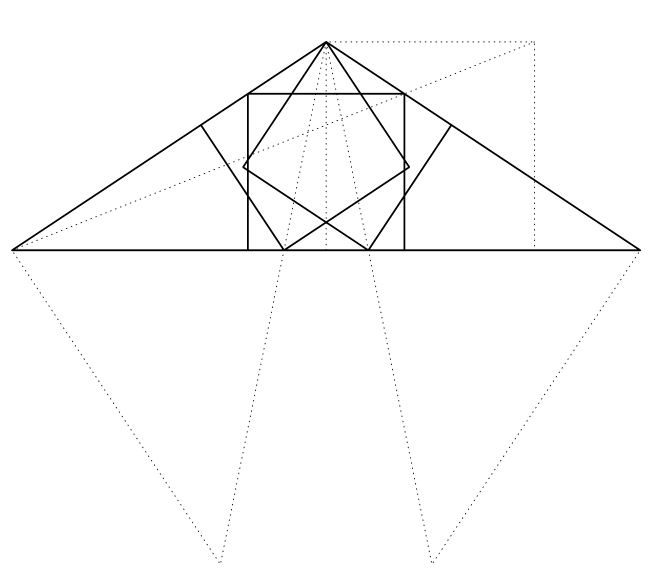
I do not understand the code that you posted (and which comes from a website in which I do not understand the language unfortunately), but if you are willing to just take the edge length ratio from [your first link](https://mathworld.wolfram.com/CalabisTriangle.html?fbclid=IwAR288tVqTHVQgGwFMScUCt7jKDRPz6PyPSPMnTxkSUwfsNLDytSVsh7hDvE), then it is rather easy to draw the thing. The inscribed squares can be constructed by computing the intersections of some 45 degree lines with the opposite edges.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}[line cap=round,line join=round,scale=5,
declare function={q=1.55139;phi=acos(q/2);}]
\draw[thick] (-1/2,0) coordinate (A) --
(1/2,0) coordinate (B) -- (0,{sin(phi)/q}) coordinate (C) -- cycle;
\draw ($(C)+(180+phi+45:0.5)$) coordinate (auxA)
(intersection of C--auxA and A--B) coordinate (p1ll)
-- ($(A)!(p1ll)!(C)$) -- (C)
let \p1=($(p1ll)-(C)$),\n1={veclen(\x1,\y1)/sqrt(2)} in
-- ++ (270+phi:\n1) -- cycle
($(C)+(-phi-45:0.5)$) coordinate (auxB)
(intersection of C--auxB and A--B) coordinate (p2ll)
-- ($(B)!(p2ll)!(C)$) -- (C)
-- ++ (-phi-90:\n1) -- cycle
(-\n1/2,0) rectangle ++ (\n1,\n1);
\end{tikzpicture}
\end{document}
```