Here is one way using the `calc` library. It introduces an auxiliary coordinate, the name of which is stored in a pgf key. The angles of the two relevant edges get measured and the auxiliary coordinate is then placed using these angles.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}
\tikzset{bisector/.style n args={3}{insert path={%
let \p1=($(#1)-(#2)$),\p2=($(#3)-(#2)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)}
in ($(#2)+(\n1/2+\n2/2:1)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name})
(#2) -- (intersection of #1--#3 and #2--\pgfkeysvalueof{/tikz/aux/name})
}},aux/.cd,name/.initial=aux}
\begin{document}
\begin{tikzpicture}
\draw (0,0) coordinate (A) -- (4,0) coordinate (B)
-- (1,3) coordinate (C) -- cycle;
\draw[purple,bisector={A}{B}{C},bisector={C}{A}{B},bisector={B}{C}{A}];
\end{tikzpicture}
\end{document}
```
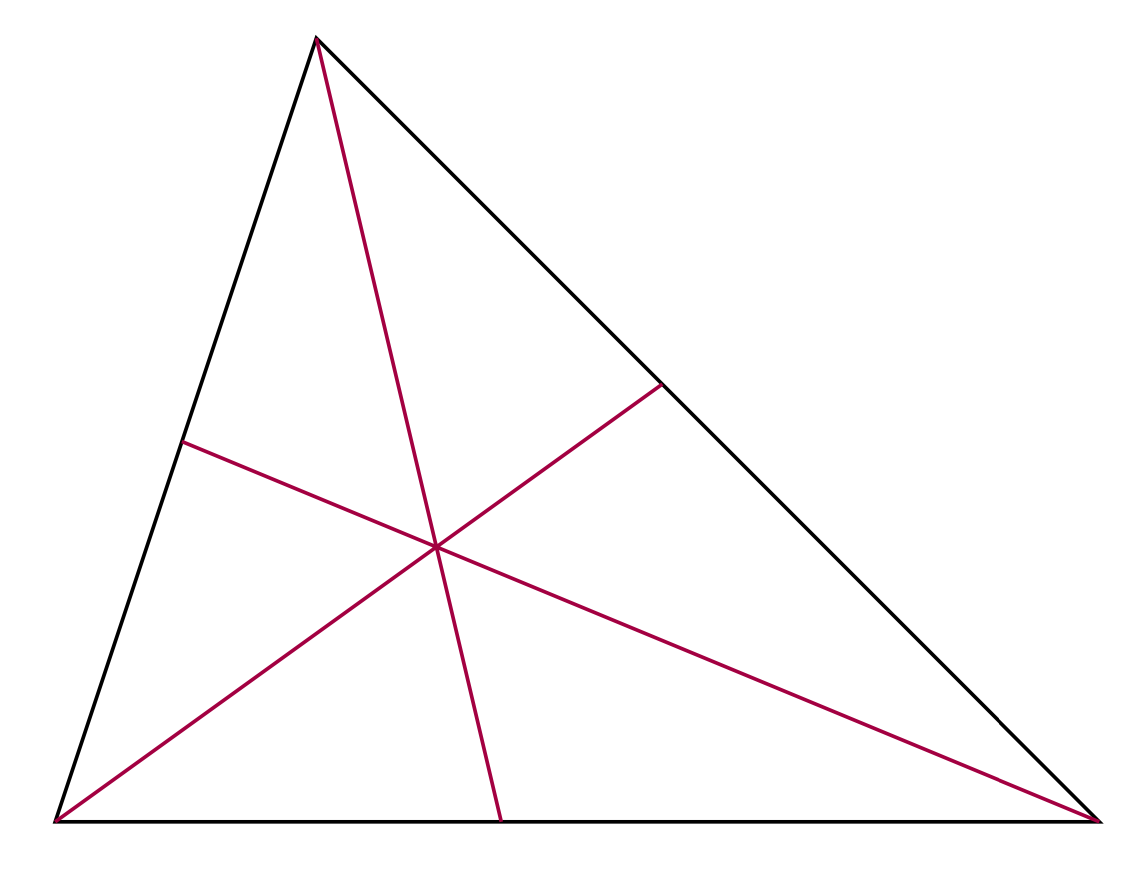
The last `\draw` command can be condensed to
```
\draw[purple,bisector/.list={{A}{B}{C},{C}{A}{B},{B}{C}{A}}];
```
The auxiliary coordinates can be used to construct the incenter as the interesection of two bisectors. The radius is simply given by the distance of the incirle to its projection on one of the edges.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}
\tikzset{bisector/.style n args={3}{insert path={%
let \p1=($(#1)-(#2)$),\p2=($(#3)-(#2)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)}
in ($(#2)+(\n1/2+\n2/2:1)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name})
(#2) -- (intersection of #1--#3 and #2--\pgfkeysvalueof{/tikz/aux/name})
}},aux/.cd,name/.initial=aux}
\begin{document}
\begin{tikzpicture}
\draw (0,0) coordinate (A) -- (4,0) coordinate (B)
-- (1,3) coordinate (C) -- cycle;
\draw[purple,aux/name=auxB,bisector={A}{B}{C},
aux/name=auxA,bisector={C}{A}{B},
aux/name=auxC,bisector={B}{C}{A}];
\draw[blue] % incenter as the intersection of two bisectors
(intersection of A--auxA and B--auxB) coordinate (incenter)
% projection of incircle center on edge B--C :
($(B)!(incenter)!(C)$) coordinate (pCB)
let \p1=($(pCB)-(incenter)$),\n1={veclen(\x1,\y1)} in
(incenter) circle[radius=\n1];
\end{tikzpicture}
\end{document}
```

Alternatively, one could just add a style for the incircle. In this style, the auxiliary coordinate is at the center of the incenter.
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}
\tikzset{bisector/.style n args={3}{insert path={%
let \p1=($(#1)-(#2)$),\p2=($(#3)-(#2)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)}
in ($(#2)+(\n1/2+\n2/2:1)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name})
(#2) -- (intersection of #1--#3 and #2--\pgfkeysvalueof{/tikz/aux/name})
}},aux/.cd,name/.initial=aux,
/tikz/incircle/.style n args={3}{%
insert path={
let \p1=($(#2)-(#1)$), \p2=($(#3)-(#1)$),\p3=($(#2)-(#3)$),
\n1={0.5*(veclen(\x1,\y1)+veclen(\x2,\y2)+veclen(\x3,\y3))},
\n2={sqrt(((\n1-veclen(\x1,\y1))/\n1))*sqrt((\n1-veclen(\x2,\y2))*(\n1-veclen(\x3,\y3)))},
\n3={veclen(\x1,\y1)}, % length #1 -- #2
\n4={veclen(\x2,\y2)}, % length #1 -- #3
\n5={veclen(\x3,\y3)}, % length #2 -- #3
\n6={\n3+\n4+\n5}
in
(${(\n5/\n6)}*(#1)+{(\n4/\n6)}*(#2)+{(\n3/\n6)}*(#3)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name}) circle[radius=\n2]
}}}
\begin{document}
\begin{tikzpicture}
\draw (0,0) coordinate (A) -- (4,0) coordinate (B)
-- (1,3) coordinate (C) -- cycle;
\draw[purple,bisector/.list={{A}{B}{C},{C}{A}{B},{B}{C}{A}}];
\draw[blue,incircle={A}{B}{C}];
\end{tikzpicture}
\end{document}
```

If you want to have the radius explicitly, you can either use the `calc` methods within a path, or define a function that computes the distance. (Note that the results do not exactly coincide because of the somewhat peculiar implementation of `veclen`. You can see this for the circumcircle radius in the following example.)
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{calc}
\tikzset{bisector/.style n args={3}{%
insert path={%
let \p1=($(#1)-(#2)$),\p2=($(#3)-(#2)$),
\n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)}
in ($(#2)+(\n1/2+\n2/2:1)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name})
(#2) -- (intersection of #1--#3 and #2--\pgfkeysvalueof{/tikz/aux/name})
}},aux/.cd,name/.initial=aux,
/tikz/incircle/.style n args={3}{%
insert path={
let \p1=($(#2)-(#1)$), \p2=($(#3)-(#1)$),\p3=($(#2)-(#3)$),
\n1={0.5*(veclen(\x1,\y1)+veclen(\x2,\y2)+veclen(\x3,\y3))},
\n2={sqrt(((\n1-veclen(\x1,\y1))/\n1))*sqrt((\n1-veclen(\x2,\y2))*(\n1-veclen(\x3,\y3)))},
\n3={veclen(\x1,\y1)}, % length #1 -- #2
\n4={veclen(\x2,\y2)}, % length #1 -- #3
\n5={veclen(\x3,\y3)}, % length #2 -- #3
\n6={\n3+\n4+\n5}
in
(${(\n5/\n6)}*(#1)+{(\n4/\n6)}*(#2)+{(\n3/\n6)}*(#3)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name}) circle[radius=\n2]
}},/tikz/circumcircle/.style n args={3}{insert path={
let \p1=(#1),\p2=(#2),\p3=(#3),
\n1={atan2(\y3-\y2,\x3-\x2)-atan2(\y1-\y2,\x1-\x2)},
\n2={veclen(\x3-\x1,\y3-\y1)*tan(\n1)/2}
in
($($(#1)!0.5!(#3)$)!\n2!90:(#3)$)
coordinate (\pgfkeysvalueof{/tikz/aux/name})
let \p4=($(#1)-(\pgfkeysvalueof{/tikz/aux/name})$),
\n4={veclen(\x4,\y4)} in
circle[radius=\n4]
}}}
\makeatletter
\pgfmathdeclarefunction{distance}{2}{%
\begingroup%
\pgfextractx{\pgf@xa}{\pgfpointanchor{#1}{center}}%
\pgfextracty{\pgf@ya}{\pgfpointanchor{#1}{center}}%
\pgfextractx{\pgf@xb}{\pgfpointanchor{#2}{center}}%
\pgfextracty{\pgf@yb}{\pgfpointanchor{#2}{center}}%
\pgfmathparse{sqrt(pow(\pgf@xa-\pgf@xb,2)+pow(\pgf@ya-\pgf@yb,2))}%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%
\makeatother
\begin{document}
\begin{tikzpicture}[>=latex]
\draw (0,0) coordinate (A) -- (4,0) coordinate (B)
-- (1,3) coordinate (C) -- cycle;
\draw[purple,bisector/.list={{A}{B}{C},{C}{A}{B},{B}{C}{A}}];
\draw[blue,aux/name=incenter,incircle={A}{B}{C}];
\draw[|<->|] ($(B)!(incenter)!(C)$) coordinate (pCB)
let \p1=($(pCB)-(incenter)$),\n1={veclen(\x1,\y1)} in
-- node[above,sloped]{\pgfmathparse{\n1/1cm}\pgfmathprintnumber\pgfmathresult}
(incenter);
\draw[red,aux/name=circumcenter,circumcircle={A}{B}{C}];
\draw[|<->|] let \p1=($(B)-(circumcenter)$),
\n1={veclen(\x1,\y1)} in
(B) -- node[above,sloped]{\pgfmathparse{\n1/1cm}\pgfmathprintnumber\pgfmathresult}
(circumcenter);
\pgfmathsetmacro{\myinradius}{distance("pCB","incenter")/1cm}
\pgfmathsetmacro{\mycircumradius}{distance("A","circumcenter")/1cm}
\typeout{The incircle radius is \myinradius, and the circumcircle radius is \mycircumradius.}
\end{tikzpicture}
\end{document}
```
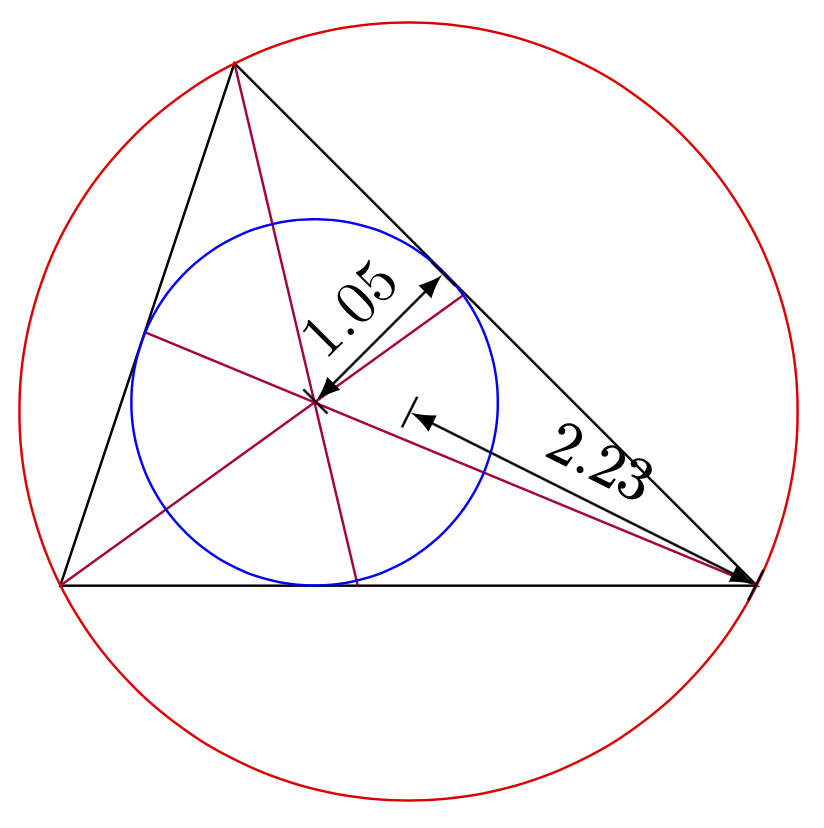
More generally, it is probably not exceedingly difficult to create styles for many of the constructions that are part of `tkz-euclide`. However, as far as I know, often the codes of `tkz-euclide` take some precautions and are also able with dealing with special cases. For instance, imagine that the user did not use a real triangle in the above examples but all three points are on a line. Then the above codes would just not work, and not tell the user what specifically is the problem. It is these special cases which are most of the work.