How to render a randomly rolled 20 sided die? - TeX

TopAnswers TeX

Top Answer

user 3.14159

Thanks to the [Mathematica code that you linked to](https://mathematica.stackexchange.com/a/55250) one can order the faces in such a way that the numbering is realistic. Some time ago I wrote some code that allows one to draw arbitrary polyhedra for arbitrary view angles with Ti*k*Z. You will need the inofficial [3dtools library](https://github.com/marmotghost/tikz-3dtools) since this code computes quite a few vector products, linear combinations and projections, which are, to the best of my knowledege, not supported by the official Ti*k*Z libraries. This works by getting the vertices and polygons bounding the faces from somewhere. One possibility is to use Mathematica with the commands (in the case at hand we want an icosahedron)
```
PolyhedronData["Icosahedron", "VertexCoordinates"]
PolyhedronData["Icosahedron", "FaceIndices"]
```
(but for the purpose of the first code I used [this link](https://mathematica.stackexchange.com/a/55250) to have opposite numbers adding up to 21) and feeding them into some otherwise identical routine, draws the faces in such a way that the "visible" ones are in the foreground and the hidden ones in the background. The visibility is decided according whether the outward-facing normal of a given polyon point out of or into the screen. These projections are computed in a "tool-independent" way, i.e. even though `tikz-3dplot` is used to define the view angles, any other tool will also work. It also manually cures some `dimension too large` errors that in the best of all worlds are taken care of already at the level of the `3d` library. They would emerge if the projection of the plane becomes so thin that the number is not readable (or even visible) anyway. This is something that definitely needs to be improved, possibly at the expense of rewriting parts of the `3d` library. 

```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{backgrounds,3dtools} % https://github.com/marmotghost/tikz-3dtools
\makeatletter
\tikzset{use fpu reciprocal/.code={%
\def\pgfmathreciprocal@##1{%
    \begingroup
    \pgfkeys{/pgf/fpu=true,/pgf/fpu/output format=fixed}%
    \pgfmathparse{1/##1}%
    \pgfmath@smuggleone\pgfmathresult
    \endgroup
}}}%
\makeatother
\tikzset{pics/icosahedron/.style={code={
\path foreach \Coord [count=\X] in 
 {(0, -1, -PHI), (0, -1, +PHI), (0, +1, -PHI), (0, +1, +PHI),
  (-1, -PHI, 0), (-1, +PHI, 0), (+1, -PHI, 0), (+1, +PHI, 0),
  (-PHI, 0, -1), (+PHI, 0, -1), (-PHI, 0, +1), (+PHI, 0, +1)}
 {\Coord coordinate (p\X) \pgfextra{\xdef\NumVertices{\X}}}; 
 %\message{number of vertices is \NumVertices^^J} 
 % "light source"
 \edef\lstPast{0}
 \foreach \poly [count=\iface] in 
 {{2, 4, 12}, 
 {2, 12, 7}, 
 {2, 7, 5}, 
 {2, 5, 11}, 
 {2, 11, 4}, 
 {4, 6, 8}, 
 {4, 8, 12}, 
 {4, 6, 11}, 
 {12, 7, 10}, 
 {12, 8, 10}, 
 {11, 9, 5}, 
 {11, 9, 6}, 
 {1, 7, 10}, 
 {1, 9, 5}, 
 {1, 7, 5}, 
 {1, 3, 10}, 
 {8, 3, 10}, 
 {6, 3, 8}, 
 {3, 9, 6}, 
 {1, 3, 9}}
 {
  \pgfmathtruncatemacro{\ione}{{\poly}[0]}
  \pgfmathtruncatemacro{\itwo}{{\poly}[2]}
  \pgfmathtruncatemacro{\ithree}{{\poly}[1]}
  \path[overlay,3d coordinate={(dA)=(p\itwo)-(p\ione)},
   3d coordinate={(dB)=(p\itwo)-(p\ithree)},
   3d coordinate={(nA)=(dA)x(dB)}] ;
  \pgfmathtruncatemacro{\jtest}{sign(TD("(nA)o(p\ione)"))}
  % make sure that the normal points outwards
  \ifnum\jtest<0
   \path[overlay,3d coordinate={(nA)=(dB)x(dA)}];
  \else % change the orientation of the basis vectors  
   \edef\idum{\ithree}%
   \edef\ithree{\itwo}%
   \edef\itwo{\idum}%
   %\typeout{reordered \iface}
  \fi
  % barycenter for triangular faces
  \pgfmathsetmacro{\mybary}{TD("0.333*(p\ione)+0.333*(p\itwo)+0.333*(p\ithree)")}
  \path[overlay] (\mybary) coordinate (bary-\iface);
  % compute projection the normal of the polygon on the normal of screen    
  \pgfmathsetmacro{\mynA}{TD("(nA)")}
  \pgfmathsetmacro\myproj{screendepth(\mynA)}
  \pgfmathsetmacro\lproj{TD("(nA)o(L)")/3}
  \pgfmathtruncatemacro{\itest}{sign(\myproj)}
  \pgfmathtruncatemacro{\cf}{70-25*\lproj}% color fraction between 50 and 90
  \ifnum\itest>-1 
   \draw[ultra thin] [fill=mypolyhedroncolor!\cf]
    plot[samples at=\poly,variable=\x](p\x) -- cycle;
   \path[3d/define orthonormal dreibein={A={(p\ione)},B={(p\itwo)},C={(p\ithree)}}];
   \path let \p1=(ex),\p2=(ey),
	\n1={min(veclen(\x1,\y1),veclen(\x2,\y2))},
	\n2={abs(\x1*\x2+\y1*\y2)},
	\n3={(\n1>3)+(\n2<333)}
	 in \pgfextra{\pgfmathtruncatemacro{\myflag}{\n3}\xdef\myflag{\myflag}};
   \ifnum\myflag=2% <- make sure that the plane is not too weird
   \begin{scope}[x={(ex)},y={(ey)},z={(ez)},canvas is xy plane at z=0]
    \path (bary-\iface) node[transform shape,text=white,
		font=\bfseries]{\FaceNum{\iface}};
   \end{scope} 
   \fi
  \else
   \begin{scope}[on background layer] 
    \draw[gray,ultra thin] [fill=mypolyhedroncolor!\cf!black]
    plot[samples at=\poly,variable=\x](p\x) -- cycle;  
   \end{scope}
  \fi
  }}}}
% this controls the number 
\newcommand\FaceNum[1]{\ifcase#1\or
	1\or2\or3\or4\or5\or6.\or7\or8\or9.\or10\or
	11\or12\or13\or14\or15\or16\or17\or18\or19\or20\fi}
\begin{document}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{70+10*cos(\Angle)}{\Angle}
\begin{tikzpicture}[tdplot_main_coords,line cap=round,line join=round,
	declare function={PHI=(1+sqrt(5))/2;}]
  \path[tdplot_screen_coords,use as bounding box] (-4,-4) rectangle (4,4);
  % light source
  \path[overlay] ({-sqrt(1/6)},{sqrt(3/6)},{sqrt(2/6)})  coordinate (L); 
  % base color 
  \colorlet{mypolyhedroncolor}{blue}
  % draw the d20
  \path[scale=2,transform shape] pic{icosahedron};
\end{tikzpicture}}
\end{document}
```
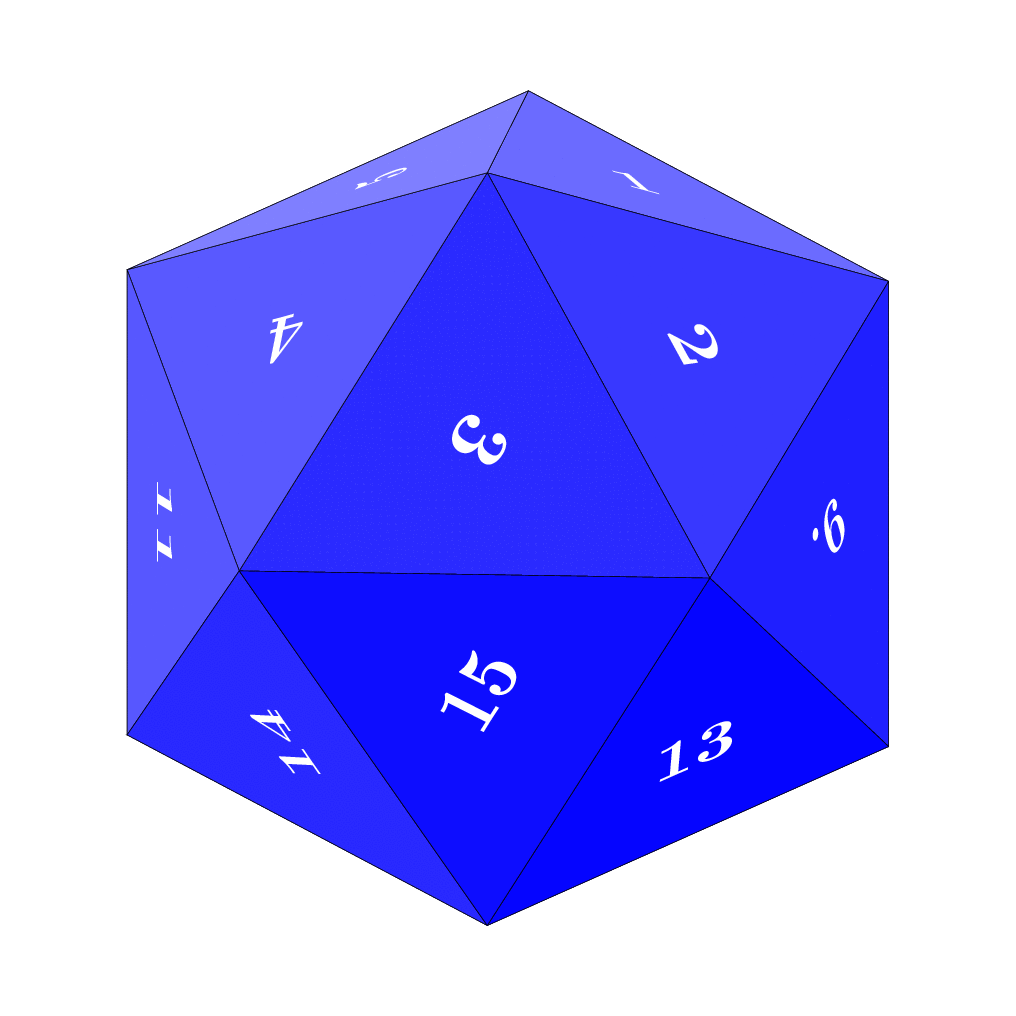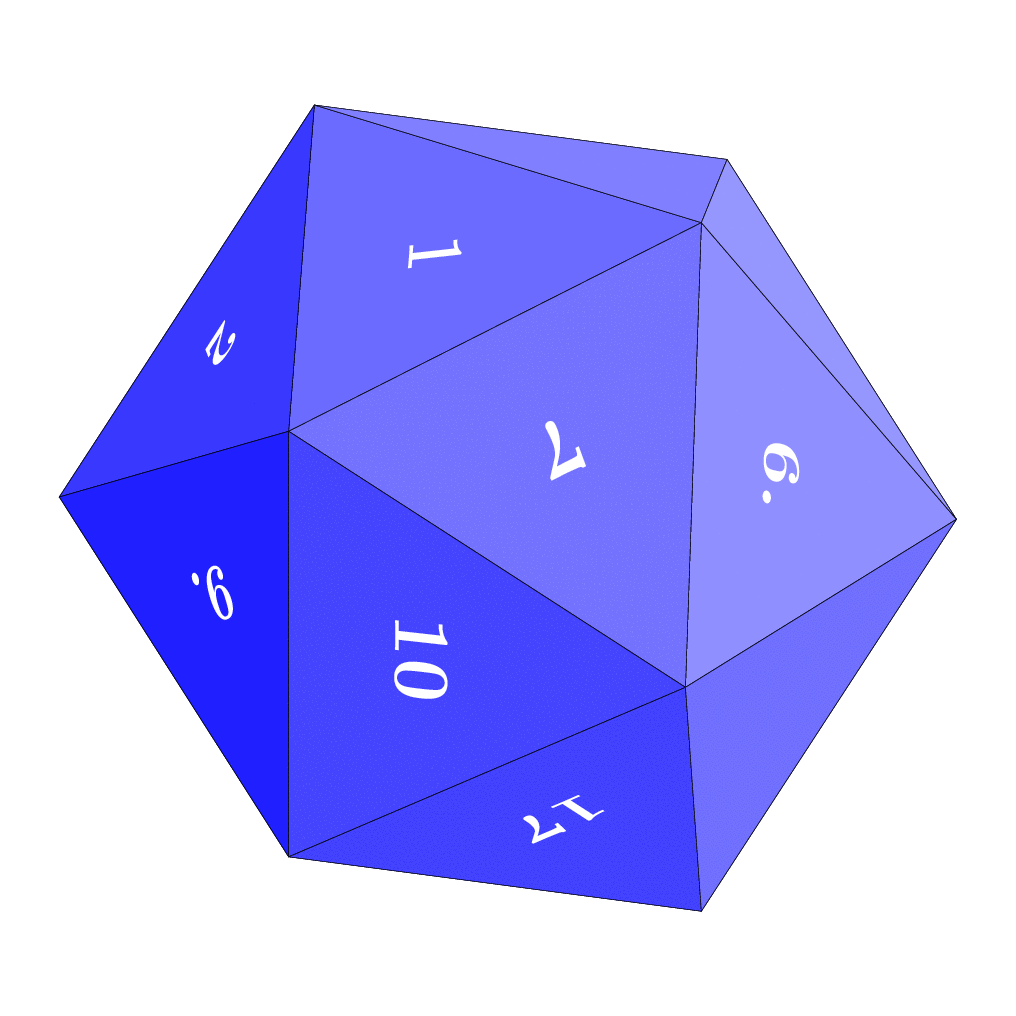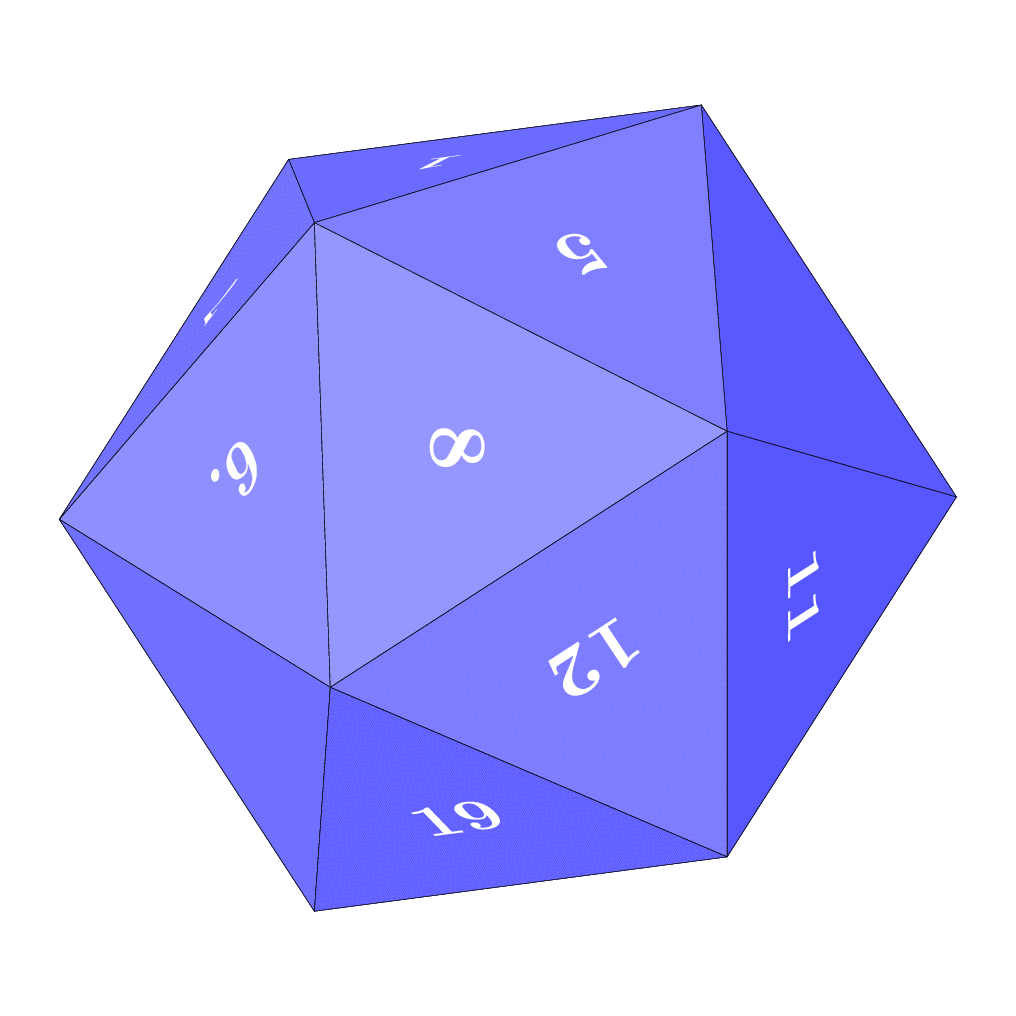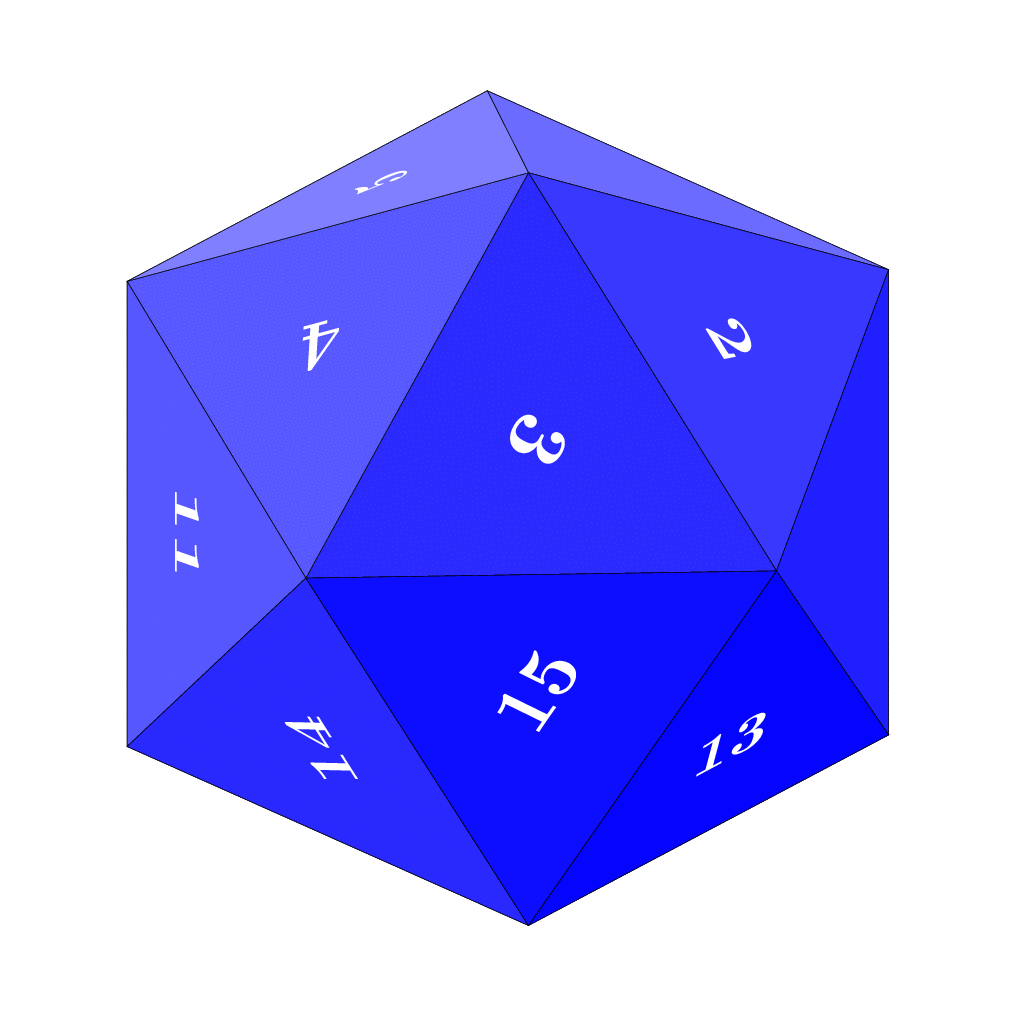
![ani.gif](/image?hash=3899684105e15042e50482e88cf47198d392cae6f38db221d53394d70bd01686)

I tried to explain things like the "light source" or the color in the code.

And here is an alternative with major support by our Ti*k*Zlings.
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikzlings}
\newcommand{\Diceling}[2][]{%
\ifcase#2
\anteater[#1]\or
\bear[#1]\or
\bee[#1]\or
\cat[#1]\or
\coati[#1]\or
\hippo[#1]\or
\koala[#1]\or
\marmot[#1]\or
\squirrel[back,#1]\or
\mouse[#1]\or
\owl[#1]\or
\panda[#1]\or
\penguin[#1]\or
\pig[#1]\or
\rhino[#1]\or
\squirrel[#1]\or
\anteater[back,#1]\or
\bear[back,#1]\or
\bee[back,#1]\or
\koala[back,#1]\or
\snowman[#1]\or
\fi}
\usepackage{tikz-3dplot}
\usetikzlibrary{backgrounds,3dtools} % https://github.com/marmotghost/tikz-3dtools
%\newcounter{tdorder}
\tikzset{pics/icosahedron/.style={code={
\path foreach \Coord [count=\X] in 
{(0., 0., -0.9510565162951536), 
 (0., 0., 0.9510565162951536), (-0.85065080835204, 
  0., -0.42532540417601994), (0.85065080835204, 0., 
  0.42532540417601994), (0.6881909602355868, -0.5, 
  -0.42532540417601994), (0.6881909602355868, 0.5, 
  -0.42532540417601994), (-0.6881909602355868, -0.5, 
  0.42532540417601994), (-0.6881909602355868, 0.5, 
  0.42532540417601994), (-0.2628655560595668, 
  -0.8090169943749475, -0.42532540417601994), 
 (-0.2628655560595668, 0.8090169943749475, 
  -0.42532540417601994), (0.2628655560595668, 
  -0.8090169943749475, 0.42532540417601994), 
 (0.2628655560595668, 0.8090169943749475, 
  0.42532540417601994)}
  {\Coord coordinate (p\X) \pgfextra{\xdef\NumVertices{\X}}};
 %\message{number of vertices is \NumVertices^^J} 
 % "light source"
 \edef\lstPast{0}
 \foreach \poly [count=\iface] in 
 {{2, 12, 8}, {2, 8, 7}, {2, 7, 11}, {2, 11, 4}, 
 {2, 4, 12}, {5, 9, 1}, {6, 5, 1}, {10, 6, 1}, 
 {3, 10, 1}, {9, 3, 1}, {12, 10, 8}, {8, 3, 7}, 
 {7, 9, 11}, {11, 5, 4}, {4, 6, 12}, {5, 11, 9}, 
 {6, 4, 5}, {10, 12, 6}, {3, 8, 10}, {9, 7, 3}}
 {
  \pgfmathtruncatemacro{\ione}{{\poly}[0]}
  \pgfmathtruncatemacro{\itwo}{{\poly}[1]}
  \pgfmathtruncatemacro{\ithree}{{\poly}[2]}
  \path[overlay,3d coordinate={(dA)=(p\itwo)-(p\ione)},
   3d coordinate={(dB)=(p\itwo)-(p\ithree)},
   3d coordinate={(nA)=(dA)x(dB)}] ;
  \pgfmathtruncatemacro{\jtest}{sign(TD("(nA)o(p\ione)"))}
  % make sure that the normal points outwards
  \ifnum\jtest<0
   \path[overlay,3d coordinate={(nA)=(dB)x(dA)}];
  \fi
  % barycenter for triangular faces
  \pgfmathsetmacro{\mybary}{TD("0.333*(p\ione)+0.333*(p\itwo)+0.333*(p\ithree)")}
  \path[overlay] (\mybary) coordinate (bary-\iface);
  % compute projection the normal of the polygon on the normal of screen    
  \pgfmathsetmacro{\mynA}{TD("(nA)")}
  \pgfmathsetmacro\myproj{screendepth(\mynA)}
  \pgfmathsetmacro\lproj{TD("(nA)o(L)")}
  \pgfmathtruncatemacro{\itest}{sign(\myproj)}
  \pgfmathtruncatemacro{\cf}{70-25*\lproj}% color fraction between 50 and 90
  \ifnum\itest>-1 
   \draw[ultra thin] [fill=mypolyhedroncolor!\cf]
    plot[samples at=\poly,variable=\x](p\x) -- cycle;
   \path[3d/define orthonormal dreibein={A={(p\ione)},B={(p\itwo)},C={(p\ithree)}}];
   \path let \p1=(ex),\p2=(ey),\p3=(ez),
	\n1={min(veclen(\x1,\y1),veclen(\x2,\y2),veclen(\x3,\y3))},
	\n2={abs(\x1*\x2+\y1*\y2)},
	\n3={(\n1>2)+(\n2<320)}
	 in \pgfextra{\pgfmathtruncatemacro{\myflag}{\n3}\xdef\myflag{\myflag}};
   \ifnum\myflag=2% <- make sure that the plane is not too weird
   \begin{scope}[x={(ex)},y={(ey)},z={(ez)},canvas is xy plane at z=0,
   	scale=0.2,shift={(bary-\iface)},shift={(0,-1)}]
    \Diceling{\iface}
   \end{scope} 
   \fi
  \else
   \begin{scope}[on background layer] 
    \draw[gray,ultra thin] [fill=mypolyhedroncolor!\cf!black]
    plot[samples at=\poly,variable=\x](p\x) -- cycle;  
   \end{scope}
  \fi
  }}}}
\begin{document}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{70+9*cos(\Angle)}{\Angle}
\begin{tikzpicture}[tdplot_main_coords,line cap=round,line join=round]
  \path[tdplot_screen_coords,use as bounding box] (-5,-5) rectangle (5,5);
  % light source
  \path[overlay] ({-sqrt(1/6)},{sqrt(3/6)},{sqrt(2/6)})  coordinate (L); 
  % base color 
  \colorlet{mypolyhedroncolor}{blue}
  % draw the d20
  \path[scale=pi,transform shape] pic{icosahedron};
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=797bc4562db3f2ff0becd8d9d023fbb0e5fd5487a1b527705c49607d33450e8a)

It is totally possible but most likely this code is a complete overkill for that as it is written to allow for arbitrary rotations. For the feature you are looking for you have always the same graphics but just different numbers projected on the various faces. Nonetheless, here is a code for that: ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{backgrounds,3dtools} % https://github.com/marmotghost/tikz-3dtools \tikzset{pics/polyhedron/.style={code={ \path foreach \Coord [count=\X] in \lstVertices {\Coord coordinate (p\X) \pgfextra{\xdef\NumVertices{\X}}}; %\message{number of vertices is \NumVertices^^J} % "light source" \foreach \poly [count=\iface] in \lstFaces { \pgfmathtruncatemacro{\ione}{{\poly}[0]} \pgfmathtruncatemacro{\itwo}{{\poly}[2]} \pgfmathtruncatemacro{\ithree}{{\poly}[1]} \path[overlay,3d coordinate={(dA)=(p\itwo)-(p\ione)}, 3d coordinate={(dB)=(p\itwo)-(p\ithree)}, 3d coordinate={(nA)=(dA)x(dB)}] ; \pgfmathtruncatemacro{\jtest}{sign(TD("(nA)o(p\ione)"))} % make sure that the normal points outwards \ifnum\jtest<0 \path[overlay,3d coordinate={(nA)=(dB)x(dA)}]; \else % change the orientation of the basis vectors \edef\idum{\ithree}% \edef\ithree{\itwo}% \edef\itwo{\idum}% %\typeout{reordered \iface} \fi \expandafter\xdef\csname tmptp\iface\endcsname{\ione,\itwo,\ithree} % barycenter for triangular faces \pgfmathsetmacro{\mybary}{TD("0.333*(p\ione)+0.333*(p\itwo)+0.333*(p\ithree)")} \path[overlay] (\mybary) coordinate (bary-\iface); % compute projection the normal of the polygon on the normal of screen \pgfmathsetmacro{\mynA}{TD("(nA)")} \pgfmathsetmacro\myproj{screendepth(\mynA)} \pgfmathsetmacro\lproj{TD("(nA)o(L)")/3} \pgfmathtruncatemacro{\itest}{sign(\myproj)} \pgfmathtruncatemacro{\cf}{70-25*\lproj}% color fraction between 50 and 90 \ifnum\itest>-1 \draw[ultra thin] [fill=mypolyhedroncolor!\cf] plot[samples at=\poly,variable=\x](p\x) -- cycle; \path[3d/define orthonormal dreibein={A={(p\ione)},B={(p\itwo)},C={(p\ithree)}}]; \path let \p1=(ex),\p2=(ey), \n1={min(veclen(\x1,\y1),veclen(\x2,\y2))}, \n2={abs(\x1*\x2+\y1*\y2)}, \n3={(\n1>3)+(\n2<333)} in \pgfextra{\pgfmathtruncatemacro{\myflag}{\n3}\xdef\myflag{\myflag}}; \ifnum\myflag=2% <- make sure that the plane is not too weird \begin{scope}[x={(ex)},y={(ey)},z={(ez)},canvas is xy plane at z=0] \path (bary-\iface) node[transform shape,text=white, font=\bfseries]{\FaceNum{\iface}}; \end{scope} \fi \else \begin{scope}[on background layer] % \draw[gray,ultra thin] [fill=mypolyhedroncolor!\cf!black] % plot[samples at=\poly,variable=\x](p\x) -- cycle; \end{scope} \fi }}}} % this controls the number \newcommand\FaceNum[1]{\ifcase#1\or 1\or2\or3\or4\or5\or6.\or7\or8\or9.\or10\or 11\or12\or13\or14\or15\or16\or17\or18\or19\or20\fi} \begin{document} \foreach \PFT in {1,...,20} {\tdplotsetmaincoords{70}{110} \begin{tikzpicture}[tdplot_main_coords,line cap=round,line join=round, declare function={PHI=(1+sqrt(5))/2;}] \edef\lstVertices{(0, -1, -PHI), (0, -1, +PHI), (0, +1, -PHI), (0, +1, +PHI), (-1, -PHI, 0), (-1, +PHI, 0), (+1, -PHI, 0), (+1, +PHI, 0), (-PHI, 0, -1), (+PHI, 0, -1), (-PHI, 0, +1), (+PHI, 0, +1)} \edef\lstFaces{{2, 4, 12}, {2, 12, 7}, {2, 7, 5}, {2, 5, 11}, {2, 11, 4}, {4, 6, 8}, {4, 8, 12}, {4, 6, 11}, {12, 7, 10}, {12, 8, 10}, {11, 9, 5}, {11, 9, 6}, {1, 7, 10}, {1, 9, 5}, {1, 7, 5}, {1, 3, 10}, {8, 3, 10}, {6, 3, 8}, {3, 9, 6}, {1, 3, 9}} \path[tdplot_screen_coords,use as bounding box] (-4,-4) rectangle (4,4); % light source \path[overlay] ({-sqrt(1/6)},{sqrt(3/6)},{sqrt(2/6)}) coordinate (L); % base color \colorlet{mypolyhedroncolor}{blue} % draw the d20 \begin{scope}[opacity=0] \path[scale=2,transform shape] pic{polyhedron}; \end{scope} \pgfmathsetmacro{\myaxisangles}{axisangles("(bary-\PFT)")}% \pgfmathsetmacro{\myphi}{{\myaxisangles}[0]} \pgfmathsetmacro{\mypsi}{{\myaxisangles}[1]} \edef\mytp{\csname tmptp\PFT\endcsname} \pgfmathsetmacro{\ione}{{\mytp}[0]} \pgfmathsetmacro{\itwo}{{\mytp}[1]} \pgfmathsetmacro{\ithree}{{\mytp}[2]} %\typeout{phi=\myphi,psi=\mypsi,i1=\ione,i2=\itwo} \begin{scope}[3d/install view={phi=\myphi,psi=\mypsi}] \pgfmathsetmacro{\myA}{TD("(p\ione)")} \pgfmathsetmacro{\myB}{TD("(p\itwo)")} \path let \p1=($(\myB)-(\myA)$),\n1={atan2(\y1,\x1)} in [scale=2,rotate=-\n1,transform shape] pic{polyhedron}; \end{scope} \end{tikzpicture}} \end{document} ```

![Screen Shot 2020-09-03 at 11.32.03 AM.png](/image?hash=31df5efadb84d7ee85ba19fe5359fea94b7984a6cef8f68fda96e2e6032d89ea) The 12 face is in the front, one would also have to find the rotation that makes it horizontal, which is possible but I think that this should go somewhere else. The main trick here is the `axisangles` function (or `\tdplotgetpolarcoords{⟨x⟩}{⟨y⟩}{⟨z⟩}` from `tikz-3dplot`) that allows us to find the necessary rotation relatively easily.)

This is a "proof of principle" version that allows you to rotate any face to the front. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{backgrounds,3dtools} % https://github.com/marmotghost/tikz-3dtools \tikzset{pics/polyhedron/.style={code={ \path foreach \Coord [count=\X] in \lstVertices {\Coord coordinate (p\X) \pgfextra{\xdef\NumVertices{\X}}}; %\message{number of vertices is \NumVertices^^J} % "light source" \foreach \poly [count=\iface] in \lstFaces { \pgfmathtruncatemacro{\ione}{{\poly}[0]} \pgfmathtruncatemacro{\itwo}{{\poly}[2]} \pgfmathtruncatemacro{\ithree}{{\poly}[1]} \path[overlay,3d coordinate={(dA)=(p\itwo)-(p\ione)}, 3d coordinate={(dB)=(p\itwo)-(p\ithree)}, 3d coordinate={(nA)=(dA)x(dB)}] ; \pgfmathtruncatemacro{\jtest}{sign(TD("(nA)o(p\ione)"))} % make sure that the normal points outwards \ifnum\jtest<0 \path[overlay,3d coordinate={(nA)=(dB)x(dA)}]; \else % change the orientation of the basis vectors \edef\idum{\ithree}% \edef\ithree{\itwo}% \edef\itwo{\idum}% %\typeout{reordered \iface} \fi % barycenter for triangular faces \pgfmathsetmacro{\mybary}{TD("0.333*(p\ione)+0.333*(p\itwo)+0.333*(p\ithree)")} \path[overlay] (\mybary) coordinate (bary-\iface); % compute projection the normal of the polygon on the normal of screen \pgfmathsetmacro{\mynA}{TD("(nA)")} \pgfmathsetmacro\myproj{screendepth(\mynA)} \pgfmathsetmacro\lproj{TD("(nA)o(L)")/3} \pgfmathtruncatemacro{\itest}{sign(\myproj)} \pgfmathtruncatemacro{\cf}{70-25*\lproj}% color fraction between 50 and 90 \ifnum\itest>-1 \draw[ultra thin] [fill=mypolyhedroncolor!\cf] plot[samples at=\poly,variable=\x](p\x) -- cycle; \path[3d/define orthonormal dreibein={A={(p\ione)},B={(p\itwo)},C={(p\ithree)}}]; \path let \p1=(ex),\p2=(ey), \n1={min(veclen(\x1,\y1),veclen(\x2,\y2))}, \n2={abs(\x1*\x2+\y1*\y2)}, \n3={(\n1>3)+(\n2<333)} in \pgfextra{\pgfmathtruncatemacro{\myflag}{\n3}\xdef\myflag{\myflag}}; \ifnum\myflag=2% <- make sure that the plane is not too weird \begin{scope}[x={(ex)},y={(ey)},z={(ez)},canvas is xy plane at z=0] \path (bary-\iface) node[transform shape,text=white, font=\bfseries]{\FaceNum{\iface}}; \end{scope} \fi \else \begin{scope}[on background layer] % \draw[gray,ultra thin] [fill=mypolyhedroncolor!\cf!black] % plot[samples at=\poly,variable=\x](p\x) -- cycle; \end{scope} \fi }}}} % this controls the number \newcommand\FaceNum[1]{\ifcase#1\or 1\or2\or3\or4\or5\or6.\or7\or8\or9.\or10\or 11\or12\or13\or14\or15\or16\or17\or18\or19\or20\fi} \begin{document} \foreach \Angle in {110}%{5,15,...,355} {\tdplotsetmaincoords{70+10*cos(\Angle)}{\Angle} \begin{tikzpicture}[tdplot_main_coords,line cap=round,line join=round, declare function={PHI=(1+sqrt(5))/2;}] \edef\lstVertices{(0, -1, -PHI), (0, -1, +PHI), (0, +1, -PHI), (0, +1, +PHI), (-1, -PHI, 0), (-1, +PHI, 0), (+1, -PHI, 0), (+1, +PHI, 0), (-PHI, 0, -1), (+PHI, 0, -1), (-PHI, 0, +1), (+PHI, 0, +1)} \edef\lstFaces{{2, 4, 12}, {2, 12, 7}, {2, 7, 5}, {2, 5, 11}, {2, 11, 4}, {4, 6, 8}, {4, 8, 12}, {4, 6, 11}, {12, 7, 10}, {12, 8, 10}, {11, 9, 5}, {11, 9, 6}, {1, 7, 10}, {1, 9, 5}, {1, 7, 5}, {1, 3, 10}, {8, 3, 10}, {6, 3, 8}, {3, 9, 6}, {1, 3, 9}} \path[tdplot_screen_coords,use as bounding box] (-4,-4) rectangle (4,4); % light source \path[overlay] ({-sqrt(1/6)},{sqrt(3/6)},{sqrt(2/6)}) coordinate (L); % base color \colorlet{mypolyhedroncolor}{blue} % draw the d20 \begin{scope}[opacity=0] \path[scale=2,transform shape] pic{polyhedron}; \end{scope} \pgfmathsetmacro{\myaxisangles}{axisangles("(bary-12)")}% \pgfmathsetmacro{\myphi}{{\myaxisangles}[0]} \pgfmathsetmacro{\mypsi}{{\myaxisangles}[1]} \begin{scope}[3d/install view={phi=\myphi,psi=\mypsi}] \path[scale=2,transform shape] pic{polyhedron}; \end{scope} \end{tikzpicture}} \end{document} ```

It should be possible to achieve this by finding the rotation that makes the axis through the center of the 12 face parallel to the normal of the screen (and possibly rotate about this normal to make sure that the 12 is readable). Perhaps a separate question is better. (BTW I do not understand " it should be right way way round too".)

Yes, you are right. It seems that the built in faces from `PolyhedronData["Icosahedron", "FaceIndices"]` preserve the orientation while the ones from the link do not. However, I believe to have fixed it now. It is the same test as the check whether the normal points inwards or outwards.

I think that in principle one could add a number of Platonic solids to the `3dtools` library. The basic routine is always the same, but needs to be polished eventually. Other than that this one needs just the lists of vertices and the `PolyhedronData["Icosahedron", "VertexCoordinates"]` as well as `PolyhedronData["Icosahedron", "FaceIndices"]` for a set of shapes. I think that questions like this one can help in figuring out what the users typically want to do with those objects so that one can provide a reasonable interface. Projecting stuff on the faces is certainly one application but I am wondering if there are others. (It would also be good to have the next version of pgf out since then one won't need ugly global macros like `\NumVertices` any more.)

I tried to make the task more convenient by adding a macro (called `\FaceNum`) that controls which number appears on which face. (One needs this anyway if one wants to add periods after 6 and 9, which one probably should.)

You need to reorder the list `{{2, 12, 8}, {2, 8, 7}, {2, 7, 11}, {2, 11, 4}, {2, 4, 12}, {5, 9, 1}, {6, 5, 1}, {10, 6, 1}, {3, 10, 1}, {9, 3, 1}, {12, 10, 8}, {8, 3, 7}, {7, 9, 11}, {11, 5, 4}, {4, 6, 12}, {5, 11, 9}, {6, 4, 5}, {10, 12, 6}, {3, 8, 10}, {9, 7, 3}}`. Let's say we keep the first entry, i.e. the face that is labeled `1`. Then we need to get the `20` right. So we need to exchange the last entry, `{9, 7, 3}`, with the entry at the position that has the number at which we want the `20`. I do not happen to have a real d20 at hand, so I do not have the relevant data. It is also tedious, and if I understand the [post samcarter linked to](https://boardgames.stackexchange.com/questions/16676/is-there-a-standard-way-to-number-the-faces-of-a-20-sided-die/16677#16677) correctly, the answer is not unique. What you could, however, try to do is to ask on the Mathematica Q & A site how to reorder the faces of `PolyhedronData["Icosahedron", "FaceIndices"]` to be consistent with the role playing conventions. It is not excluded that among the Mathematica freaks there are some role playing enthusiasts.

In case anyone is wondering in which way the numberers are ordered on the dice, there is a sketch at https://boardgames.stackexchange.com/questions/16676/is-there-a-standard-way-to-number-the-faces-of-a-20-sided-die/16677#16677

1 Answer