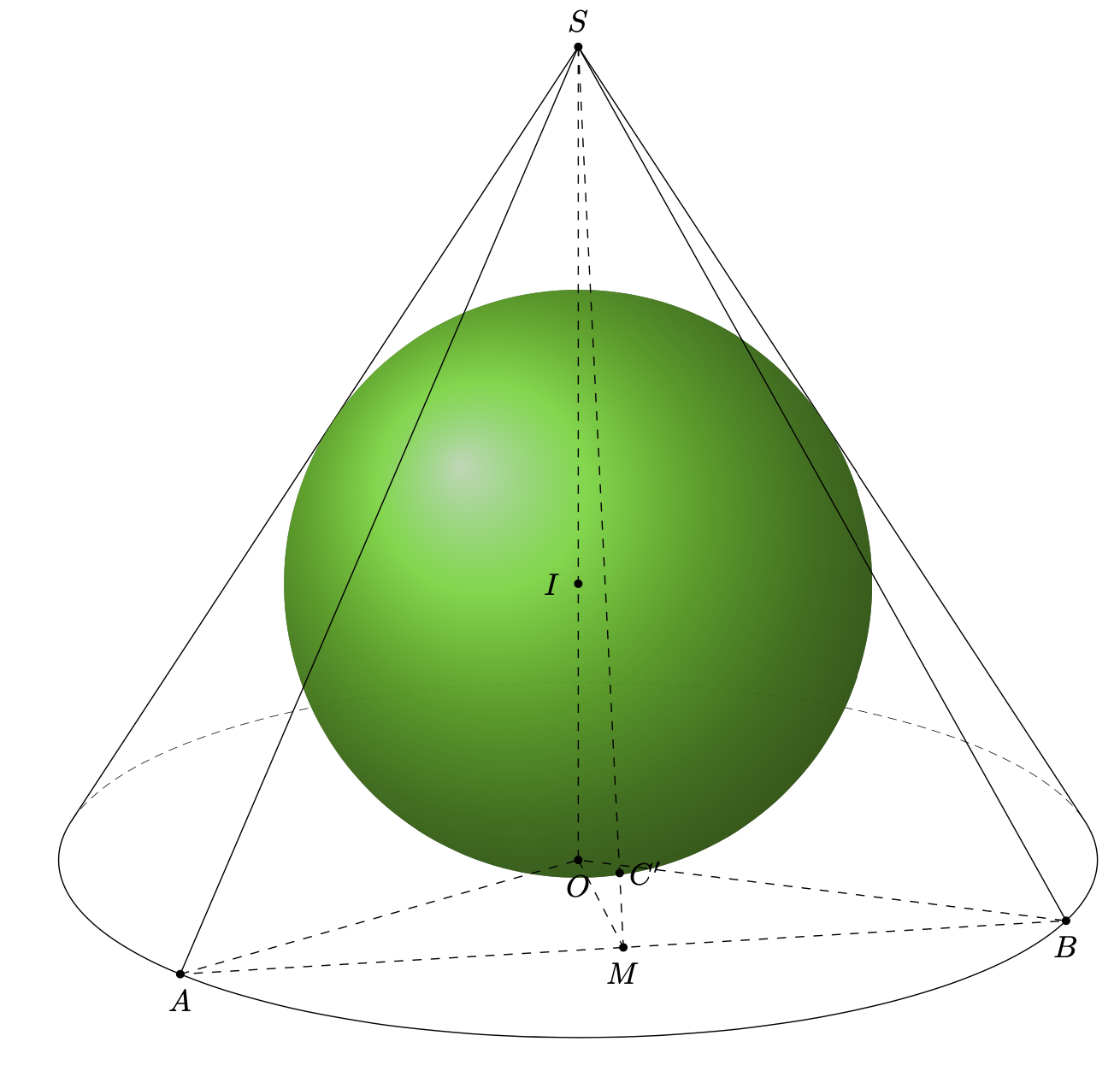
I think that in principle everything works as it should. There are two things that need to get corrected:
1. You define the coordinate `(M)` with the `calc` syntax. However, this does *not* define a 3d coordinate. (I do agree that it would make a lot of sense to make `calc` work with 3d coordinates. This will, however, require to record the screen depth of every coordinate, something that can only be implemented with major efforts and only if the pgf maintainers support it.)
2. You compute the projection outside the scope in which the `tdplot_main_coords` are set, so even if the 3d coordinates are computed correctly, the point will be off.

Fixing these issues yields a code that produces the correct result. Please note that I also added in the comments a code leading to the typeout 
```
(A)=(5.19618,-3.0,0.0),(B)=(0.0,6.0,0.0),(M)=(2.59808,1.5,0.0),(S)=(0.0,0.0,10.
0),(C')=(2.38358,1.37616,0.82565)
```
which can be used to verify the result of the computation. Indeed, `((S)-(M)).(C')<10^{-3}`, so the result is correct within the expected accuracy.

```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\tikzset{pics/3d/cone/.style={code={
	\tikzset{3d/cone/.cd,#1}
	\def\pv##1{\pgfkeysvalueof{/tikz/3d/cone/##1}}%
	\pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})}
	\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))}
	\path (0,0,\pv{h}) coordinate (-tip);
    \begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}]
	 \pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{r}/\pv{h})<1}
	 \ifnum\itest=1
	  \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})}
	  \ifdim\sdtip pt>0pt
	   \path[/tikz/3d/cone/hidden] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end
	   angle=-\alphacrit,radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   arc[start angle=\alphacrit,end  angle=360-\alphacrit,radius=\pv{r}]
	   -- (-tip) -- cycle;
	  \else
	   \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   -- (-tip) -- (360-\alphacrit:\pv{r});
	  \fi
	 \else
	  \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];	 
	 \fi
    \end{scope}
	}},
	3d/cone/.cd,r/.initial=1,h/.initial=1,
	hidden/.style={draw,very thin,densely dashed},
	visible/.style=draw}
\begin{document}
\begin{tikzpicture}[,declare function={
	r=6;h=10;rs=(r*sqrt(h^2+r^2)-r^2)/h);
	a = -30;b=a + acos(-1/2);}]
\tdplotsetmaincoords{70}{110}
\begin{scope}[tdplot_main_coords]
 \pic{3d/cone={r=r,h=h}};
 \path (0,0,rs) coordinate (I)
 (0,0,0) coordinate (O)
 (0,0,h) coordinate (S)
 ({r*cos(a)}, {r*sin(a)},0) coordinate (A)
 ({r*cos(b)}, {r*sin(b)},0) coordinate (B)
 [3d coordinate={(M)=0.5*(A)+0.5*(B)}];
 \path[3d/line through={(S) and (M) named lSM}];
 \path[3d/project={(O) on lSM}] coordinate (C');	
%  \pgfmathsetmacro{\myA}{TD("(A)")}
%  \pgfmathsetmacro{\myB}{TD("(B)")}
%  \pgfmathsetmacro{\myM}{TD("(M)")}
%  \pgfmathsetmacro{\myS}{TD("(S)")}
%  \pgfmathsetmacro{\myCprime}{TD("(C')")}
%  \pgfmathsetmacro{\mytst}{TD("(C')o(M)-(S)")}
%  \typeout{(A)=(\myA),(B)=(\myB),(M)=(\myM),(S)=(\myS),(C')=(\myCprime),check:\mytst}
\end{scope}
\begin{scope}[tdplot_screen_coords] 
\fill[ball color=green, opacity=0.8] (I) circle (rs);
\end{scope}
\foreach \p in {I,A,B,M,S,O,C'}
\draw[fill=black] (\p) circle (1.2 pt);
\foreach \p/\g in {I/180,A/-90,B/-90,M/-90,S/90,O/-90,C'/0}
\path (\p)+(\g:3mm) node{$\p$};
\draw (S) -- (A) (S) -- (B);
\draw[dashed] (S) -- (O) (A) -- (O) -- (B) -- cycle  (S) -- (M) (O) -- (M) ;
\end{tikzpicture}
\end{document}
```
![Screen Shot 2020-08-27 at 5.24.16 PM.png](/image?hash=bcd031040c6408feb723bc1128ef931e2ca535eb05185277e0aeccf16e9116f7)