First of all, as remarked in the comments the problem is that you draw the circle in screen coordinates, but you are supposed to draw it in 3d coordinates. Moving the path that contains the circle `pic` inside the `scope` fixes this problem.

As for the discrimination between hidden and visible stretches: the situation here matches precisely what one finds on pages 7-8 of the (current version of the) [3dtools manual](https://github.com/marmotghost/tikz-3dtools/blob/master/3DToolsManual.pdf), so we can copy the critical angle literally from there. Of course, one has to account for the `phi` angle that you choose nontrivial, but this just amounts to adding `\tdplotmainphi` to all angles (or, alternatively, rotating the plane). 

```
\documentclass[tikz, border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
\tdplotsetmaincoords{70}{100}
\begin{tikzpicture}[tdplot_main_coords]
	\path (-5/2, -15/8, -5/2) coordinate (A)
	(5/2, -15/8, -5/2) coordinate (B) 
	(5/2, 15/8, -5/2) coordinate (D) 
	(11/10, 117/40, -5/2) coordinate (C) 
	(-5/2, -15/8, 5/2) coordinate (S); 
	\path[3d/circumsphere center={A={(A)},B={(B)},C={(C)},D={(S)}}] 
	coordinate (I);  
% 	\path pic[draw=none]{3d circle through 3 points={%
% 			A={(A)},B={(B)},C={(C)},center name=MM}};
	\path[3d/circumcircle center={A={(A)},B={(B)},C={(C)}}]		
	coordinate (MM);
	% radius
	\pgfmathsetmacro{\myR}{sqrt(TD("(A)-(I)o(A)-(I)"))}
	% height
	\pgfmathsetmacro{\myh}{sqrt(TD("(MM)-(I)o(MM)-(I)"))}
	%
	\pgfmathsetmacro{\myr}{sqrt(TD("(A)-(MM)o(A)-(MM)"))}
	\pgfmathsetmacro{\betacrit}{asin(-\myh/\myR*cot(\tdplotmaintheta))}
	\typeout{\myr,\myh,\tdplotmaintheta,\betacrit}		
	\begin{scope}[canvas is xy plane at z=-\myh]
	 \draw[dashed] (\betacrit+\tdplotmainphi:\myr)
	  arc[start angle=\betacrit+\tdplotmainphi,
	  	end angle=180-\betacrit+\tdplotmainphi,
		radius=\myr];
	 \draw (\betacrit+\tdplotmainphi:\myr)
	  arc[start angle=\betacrit+\tdplotmainphi,
	  	end angle=-180-\betacrit+\tdplotmainphi,
		radius=\myr];
	\end{scope}
	\draw[tdplot_screen_coords] (I) circle[radius=\myR];
	\foreach \p in {A,B,C,D,S,I}
	{\draw[fill=black] (\p) circle (1.5pt);}
	\foreach \p/\g in {A/155,C/-60,B/-135,D/-45,S/0,I/-90}
	{\path (\p)+(\g:3mm) node{$\p$};}
	\foreach \X in {A,B,C,D} 
	{\draw[dashed] (\X) -- (S);}
	\draw[dashed] (A) -- (B) -- (C) -- cycle (B) -- (D) (A) -- (D);
\end{tikzpicture}
\end{document}
```
![Screen Shot 2020-08-22 at 1.09.09 PM.png](/image?hash=488c32e2ba0f6a30dda8626bf101ec564a67608c7d9a9813e5574c1b07f97680)

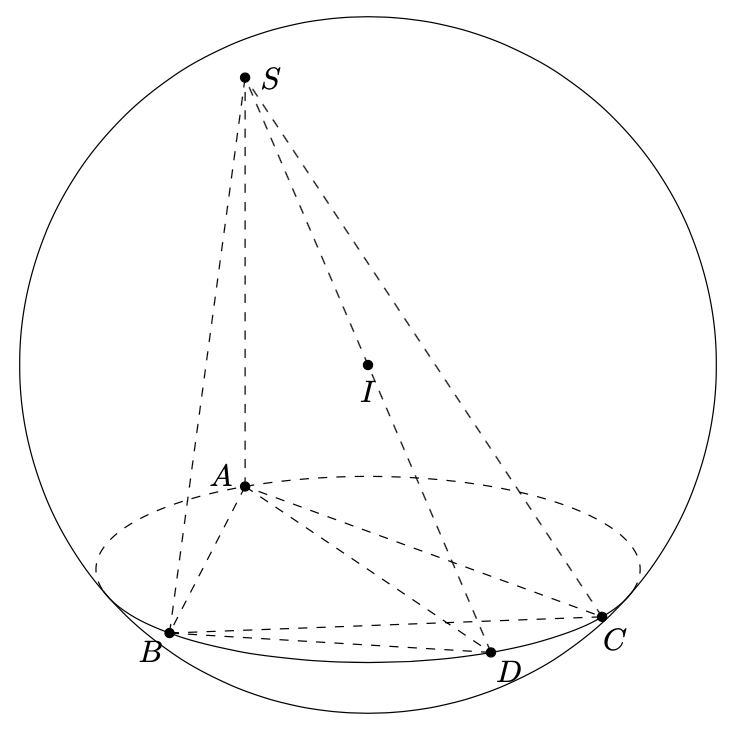
Here are some comments:
1. The current version of `3dtools` is a mess since the center of a circumscribed sphere is an `insert path` key whereas the circle through three points is a `pic`. This needs to be cleaned up. For the time being I added a key `circumcircle center`. (I find the [Wikipedia derivation](https://en.wikipedia.org/wiki/Circumscribed_circle) unnecessarily complicated so I did my own, see below.)  Any suggestion how to resolve this conundrum will be appreciated.
2. The `tikz-3dplot-circleofsphere` computes all the critical angles for circles on a sphere. Copying these would be immoral. So at this point I do not see any rasonable way of adding those to the functionality of `3dtools`.

For completeness, this is the derivation employed by the `circumcircle center` key.
![Screen Shot 2020-08-22 at 3.09.33 PM.png](/image?hash=05852d3b7caf926ba45a13db9f197a1d8c100d963d8fd704238d63ac4a4a968d)
```
\documentclass[fleqn]{article}
\usepackage[margin=1in]{geometry}
\usepackage{amsmath}
\usepackage{tikz}
\usetikzlibrary{3dtools}% https://github.com/marmotghost/tikz-3dtools
\begin{document}
Given three noncoplanar points $A$, $B$ and $C$, the center $I$ of a circle
through these points is at the intersection of two planes in the middle
between two given points, and lies in the plane spanned by those points. 
To simplify the discussion a bit, it helps to shift the coordinate system
so that the origin is $\vec A$. In these coordinates
\[\vec A\,'=0\;,\quad
\vec B\,'=\vec B-\vec A\;,\quad
\vec C\,'=\vec C-\vec A\quad\text{and}\quad
\vec I\,'=\vec I-\vec A\;.
\] 
So the conditions that $\vec I'$ is in the middle of the planes with normals
$\vec B\,'$ and $\vec C\,'$, respectively, amounts to requiring that
\[
 \vec B\,'\cdot\vec I\,'=|\vec B\,'|^2/2
 \quad\text{and}\quad
 \vec C\,'\cdot\vec I\,'=|\vec C\,'|^2/2\;.
\]
Since $\vec I\,'$ is in the plane spanned by $\vec B'$ and $\vec C'$
\[
 \vec I\,'=\beta\,\vec B\,'+\gamma\,\vec C\,'
\]
for some real $\beta$ and $\gamma$. Inserting this in the previous equation
yields
\begin{align*}
 \beta\,|\vec B\,'|^2+\gamma\,\vec B\,'\cdot\vec C\,'=|\vec B\,'|^2/2\;,\\
 \beta\,\vec B\,'\cdot\vec C\,'+\gamma\,|\vec C\,'|^2=|\vec C\,'|^2/2\;,
\end{align*}
which has the solution
\begin{align*}
 \beta=\frac{1}{2\left[|\vec B\,'|^2|\vec C\,'|^2-2\left(\vec B\,'\cdot\vec
 C\,'\right)^2\right]}
 \left(|\vec B\,'|^2-\vec B\,'\cdot\vec C\,'\right)
 |\vec C\,'|^2/2\;,\\
 \gamma=\frac{1}{2\left[|\vec B\,'|^2|\vec C\,'|^2-2\left(\vec B\,'\cdot\vec
 C\,'\right)^2\right]}
 \left(|\vec C\,'|^2-\vec B\,'\cdot\vec C\,'\right)
 |\vec B\,'|^2/2\;.
\end{align*}
With those, the solution is in the original coordinate system is given by
\[
 \vec I=\vec A+\beta\,\vec B\,'+\gamma\,\vec C\,'\;.
\]
An example is shown in figure~\ref{fig:circumcircle}.
\begin{figure}[h]
\centering
\begin{tikzpicture}[declare function={a=3;},
	dot/.style={circle,inner sep=1pt,fill},
	3d/install view={phi=100,psi=0,theta=70}]	
  \path (a,0,0) coordinate (A)
   (0,a,0) coordinate (B)
   (0,0,a) coordinate (C);
  \path[3d/circumcircle center] coordinate (I); 
  \pgfmathsetmacro{\myr}{sqrt(TD("(A)-(I)o(A)-(I)"))}
  % construct two orthogonal vectors that span the plane of the circle
  \path[overlay,
 	 3d coordinate={(n)=(B)-(I)x(C)-(I)},
	 3d coordinate={(ex')=(A)-(I)},
	 3d coordinate={(ey')=(ex')x(n)}];
  \pgfmathsetmacro{\nx}{1/sqrt(TD("(ex')o(ex')"))}
  \pgfmathsetmacro{\ny}{1/sqrt(TD("(ey')o(ey')"))}
  % construct normalized basis vectors
  \path[overlay,
	 3d coordinate={(ex)=\nx*(ex')},
	 3d coordinate={(ey)=\ny*(ey')}];
  % draw the circle	 
  \begin{scope}[x={(ex)},y={(ey)}]
   \draw (I) circle[radius=\myr];
  \end{scope}
  \path foreach \X in {A,B,C}
  {(\X) coordinate[dot,label=above:{$\X$}]}
  (I) (I) coordinate[dot,label=above:{$I=\pgfmathparse{TD("(I)")}%
   (\pgfmathprintvector\pgfmathresult)^T$}];
\end{tikzpicture}
\caption{Example of a circumcircle computation.}
\label{fig:circumcircle}
\end{figure}
\end{document}
```